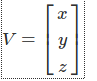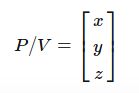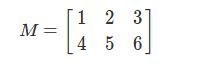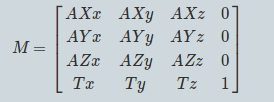零基础学图形学(9) 几何知识——行向量和列向量
在之前的文章中,我们已经解释了向量可以写成[1 x 3]的矩阵(一行三列)。但是现在也可以写成[3 x 1](三行一列)的形式。从技术上来说,这两种表示点和向量的方式都是合理的,选用一种模式只是涉及到习惯的问题。
向量写成[1 x 3]的矩阵 V = [x y z]
向量写成[3 x 1]的矩阵
在第一个例子中,我们写了一个[1 x 3]的矩阵,我们称之为行顺序(row-major order):向量被写作一行三个数据。在第二个例子中,我们称点或者是向量为列顺序(column-major order):点或者是向量的三个坐标被写成一列。
记住我们表达点或者是向量使用矩阵去乘以一个[3 x 3]的变换矩阵(为了简单起见我们使用[3 x 3]的矩阵而不是[4 x 4]的矩阵)。我们也学习到只有左边矩阵的列数等于右边矩阵的行数的时候这两个矩阵才可以相乘。换句话说也就是[m x p][ p x n]的两个矩阵可以相乘,而[p x m][p x n]的两个矩阵不可以相乘。记住我们可以将一个向量写成[1 x 3],那么它可以和一个[3 x 3]的矩阵相乘,但是如果我们把这个向量写成[3 x 1]那么我们不能和一个[3 x 3]的矩阵相乘。这个道理会在下面的例子中显示。绿色的维数是一样的所以这个乘积是合法的(所得到的结果就是一个变换的点的坐标,它的形式是一个[1 x 3]的矩阵):
里面的维数为(1和3)的两个矩阵在乘法中国因此这个成绩是不可能实现的:
那么我们应该怎么办?这个问题的答案不在是向量或者点去乘以矩阵,而是矩阵M去乘以向量V。换句话说,我们将点移动,或者向量移动到乘法的右边:
记住这个操作所得到的移动的点写成[3 x 1]的矩阵方式。因此我们可以用我们想要的方式去获得一个变换的点。问题解决了,总结一下,当习惯的时候我们表达点或者向量是用的行顺序[1 x 3],我们需要将点防止在乘法的左边,[3 x 3]的矩阵应该放置在乘法的右边。在数学上,这叫做左或者提前乘法(pre-multiplication).如果你决定将向量写成列顺序,那么点应该放置在乘法的右边,这个叫做右或者是后置乘法(post-multiplication).
我们应该对这些东西的使用格外的小心。比如,在Maya中,矩阵是后置乘法的,比如将一个点p从物体坐标系中移动到世界坐标系中,你需要的是后置的乘法P = P x WM.这是很迷惑人的,因为他实际上是提前乘法,但是他们说这个是以矩阵的位置来确定这个乘法的。在术语上这个实际上是不准确的。在Maya中,点和向量应该表达称行顺序,因此它们是属于提前乘法的(意味着点和向量出现在矩阵的之前)。
下面的这个表格总结了这两种惯例的不同之处(P表示点,V表示向量,M代表矩阵)。
行顺序 P / V = [x y z] 左或者前置乘法 P / V * M
现在我们学习了两种常规表达方式,你可能会问,为什么不把它们写在纸上?我们知道如何计算两个向量的乘积:A向量的当前行乘以相对应的B向量的当前列然后将这些结果相加。让我们运用这个公司去比较它们的结果:
行顺序(row-major order)
列顺序(column-major order)
点或者是向量和矩阵相乘不论是用行顺序还是列顺序我们都应该得到相同的结果。如果你在一个3D应用中,我们将一个点绕Z轴旋转一定的角度,你期望通过旋转之后的点在确定的位置上,不论开发者是用什么样的的方式表达点或者向量。但是,当你看到上面的表格之后,乘以一个行顺序或者是列顺序的矩阵我们不会得到相同的结果。回到我们的原点中,我们需要转置一个[3 x 3]的矩阵使它用在列向量中,从而确保x', y', z'是一样的结(如果你需要知道矩阵的转置是什么,请看矩阵操作章节),这里我们得到的:
行顺序
列顺序
总结来说,从行顺序到列顺序中不仅仅是变换了点和向量相对于乘法的位置而且将[3 x 3]的矩阵转置,这样做确保两个得到的结果是一样的。
从这些观察中可以得到,你可以将一系列的变换应用于一个点,当你使用行顺序的时候它们可以被写成一个阅读的顺序。比如你想将点P通过点T平移,然后绕Z轴旋转,然后绕y轴旋转。你可以写成下面的样式:
如果你使用一个列顺序的话,你需要调用这些变换使用相反的顺序,如下面的样子:
因此你可能回想,这里肯定有一个原因更会喜欢一种。实际上,这两种习惯都是正确的,会给我们相同的答案,但是因为一些技术上的原因,数学和物理偏向于使用列向量。
使用列向量进行变换个何如我们写的数学公式。
行矩阵可以使得我们的矩阵更简单,因此对于这个教学网站来说我们使用它(和Maya, DirectX是一样的它们也在标准手册中定义了相关习惯)。但是对于另外一些3D的api,比如opengl, 使用的是列顺序习惯。
(1)隐式编程:它影响性能吗?
这里有一个潜在的很重要的需要考虑的当你使用行顺序或者是列顺序的时候,但是这个对于真正的习惯并没有什么用处,哪个更实用。它有跟多的使用电脑的工作方式。记住我们将会处理[4 x 4]的矩阵,典型的C++实现的矩阵是下面这个样子:
class Matrix44 {
float m[4][4]
}// row-major order
x' = x * c00 + y * c10 + z * c20
y' = x * c01 + y * c11 + z * c21
z' = x * c02 + y * c12 + z * c22 // column-major order
x' = c00 * x + c01 * y + c02 * z
y' = c10 * x + c11 * y + c12 * z
z' = c20 * x + c21 * y + c22 * z template
class Vec3 {
public:
Vec3(T xx, T yy, T zz) : x(xx), y(yy), z(zz) { }
T x, y, z, w;
};
#include
#define ROWMAJOR 1
template
class Matrix44 {
public:
T m[4][4];
Vec3 multVecMatrix(const Vec3 &v) {
#ifdef ROWMAJOR
return Vec3(v.x * m[0][0] + v.y * m[1][0] + v.z * m[2][0],
v.x * m[0][1] + v.y * m[1][1] + v.z * m[2][1],
v.x * m[0][2] + v.y * m[1][2] + v.z * m[2][2]);
#else
return Vec3(v.x * m[0][0] + v.y * m[0][1] + v.z * m[0][2],
v.x * m[1][0] + v.y * m[1][1] + v.z * m[1][2],
v.x * m[2][0] + v.y * m[2][1] + v.z * m[2][2]);
#endif
}
};
#include
#include
#include
#include
#define MAX_ITER 10e8
int main(int argc, char **argv) {
clock_t start = clock();
Vec3 v(1, 2, 3);
Matrix44 M;
float *tmp = &M.m[0][0];
for (int i = 0; i < 16; i++)
*(tmp + i) = drand48();
for (int i = 0; i < MAX_ITER; ++i) {
Vec3 vt = M.multVecMatrix(v);
}
fprintf(stderr, "Clock time %f\n", (clock() - start) / float(CLOCKS_PER_SEC));
return 0;
} 两者运行时间基本上一致
wang@wang:~/workspace/graphic$ ./multiMatrix
Clock time 14.660049
wang@wang:~/workspace/graphic$ g++ -std=c++11 multiMatrix.cpp -o multiMatrix
wang@wang:~/workspace/graphic$ ./multiMatrix
Clock time 14.597244(2)计算中的行顺序和列顺序
为了完整性,行顺序和列顺序可以用于计算中,用来描述多维数组的元素在内存中的分布。在行顺序中,多维数组的元素排列从左到右,从上到下。可以使用C/c++表示他们。比如,矩阵
可以写成代码的方式:
float m[2][3]={{1, 2, 3}, {4, 5, 6}}; 1 2 3 4 5 6
在列向量中,它用在Fortran和matlab中,元素的在内存中的排列方式是从上到下,从左到右的。使用上面的矩阵,那么矩阵按照下面的方式存储:
1 4 2 5 3 6
知道矩阵中的元素在内存中是如何存放的是很重要的,因为有时候你会使用指针的偏移去获取他们。对于循环的优化(之前的小节中我们已经讲到它会影响到cpu的缓存性能)。但是,因为我们只考虑c/c++作为我们的编程语言,列顺序我们没有多大的兴趣。我们仅仅只是在计算中提到它们是什么,因此你可能会根据具体的语义去描述它们。你应该不能将它们混合。在数学上,它们描述你是用行向量,还是列向量。在计算上,它们描述了数据的储存或者获取方式。
Opengl是一个很有趣的例子,当GL初始化的时候,开发者选用行向量。开发者开发新功能的时候又要回到列向量中。但是,为了兼容性,它们不想改变点和矩阵的成绩,而是去改变矩阵在内存中存储的顺序。换句话说,opengl存储参数使用的列顺序, 参数m03, m13, m23,使用列向量会有13, 14, 14的下标识,而在行向量中有m30, m31, m32的标识。
(3)总结
下面对行向量和列向量这两种用法进行总结:
上面的英语不难,应该能看懂。
一个肚子在Stackoverflow上提了一个上面表格的问题,认为它很容易使人迷惑。这个话题是迷惑的,尽管我们已经尽了最大的努力,许多人对于它们还是感到迷惑。我们希望我们在Stackoverflow上的回答可以让读者从另一个视角来看待这个问题。
你已经有理论,你现在要做的是用C++实现它,这里有两个不同的问题。
数学上的:你可以些两种方式,可以是列顺序也可以是行顺序,如果使用行顺序,你应该将向量和矩阵的乘法写成vM,这里的表示(1 x 4)的向量,M表示(4 x 4)的矩阵。因为只有写成[1 x 4]*[4 x 4]才能进行矩阵的计算。相似地如果你想使用列顺序,你的向量应该写成竖直的,[4 x 1],因此矩阵的乘法应该写成这种样式:[4 x 4] *[4 x 1].矩阵防止在向量的前面Mv.前面一种方式叫做后置乘法,后面一种Mv叫做前置乘法(矩阵在前面)。
现在,你需要编一个一个向量或者是点,你需要注意矩阵乘法的顺序,当你把它们写在纸上的时候。如果你使用矩阵T进行平移,然后使用矩阵R进行旋转,然后使用S进行缩放变换,如果使用列矩阵的话,应该写成下面这个样式: v' = S * R * T * v。在行矩阵中你应该写成v' = v * T * R * S.
这是理论上的,我们把它叫做行/列矩阵常用习惯。
计算机上的:这关系到你如果用C++实现它们。好的消息是C++不会给你增加任何的显示。你可以将你的矩阵的参数用你想的方式放置它们,你可以自己些代码表示矩阵的乘法。相似的,你获取向量矩阵乘法的参数的操作也是取决于你。你应该做出一个清晰的区别你的矩阵参数如何放在内存中,以及你将使用那种数学习惯看待你的向量。这两个独立的问题,我们把这个叫做行/列分布。
比如,你可以定义个矩阵类有16个连续的浮点数据。那是好的,这里的参数,m14, m24, m34表示的矩阵平移的(Tx, Ty, Tz).因此这是一种列矩阵,尽然你被告知Opengl使用的矩阵是列矩阵。这里有一个很容易迷惑的就是将参数放置在内存中,不同于你实际想要表达的列矩阵。你写成行的形式,但实际上它们是列的,因此你不知道你时候在做正确的事情。
这里很重要的是,矩阵表示一个坐标系统的三根轴。哪里以及如何存储这些数据完全取决于你。想象一些三个向量表示坐标系统的三根轴,其中它们命名AX(x, y, z), AY(x, y, z), AZ(x, y,z)已经它们的平移向量表达称(Tx, Ty, Tz),那么从数学上你可以使用列向量表示
这些轴被写成竖直的形式。现在你如果使用行向量,那么可以写成如下的形式:
它的坐标系统的轴是横向的。因此接下来的问题是你的电脑如何存储这些数据的问题。你可以用下面的形式:
float m[16] = {
AXx, AXy, AXz, 0,
AYx, AYy, AYz, 0,
AZx, AZy, AZz, 0,
Tx, Ty, Tz, 1};float m[16] = {
AXx, AXy, AXz, Tx,
AYx, AYy, AYz, Ty,
AZx, AZy, AZz, Tz,
0, 0, 0, 1}; float m[16] = {
AXx, AYx, AZx, Tx,
AXy, AYy, AZy, Ty,
AXz, AYz, AZz, Tz,
0, 0, 0, 1}; Vector3 vecMatMult (
Vector3 v,
float AXx, float AXy, float AXz, float Tx,
float AYx, float AYy, float AYz, float Ty,
float AZx, float AZy, float AZz, float Tz)
{
return Vector3(
v.x * AXx + v.y * AYx + v.z * AZx + Tx,
v.x * AXy + v.y * AYy + v.z * AZy + Ty,
v.x * AXz + v.y * AZz + v.z * AZz + Tz
} float m[16] = {
AXx, AXy, AXz, 0,
AYx, AYy, AYz, 0,
AZx, AZy, AZz, 0,
Tx, Ty, Tz, 1}; vecMatMult(v, m[0], m[1], m[2], m[12], m[4], m[5], m[6], m[13], ... 如果矩阵为
float m[16] = {
AXx, AYx, AZx, Tx,
AXy, AYy, AZy, Ty,
AXz, AYz, AZz, Tz,
0, 0, 0, 1}; vecMatMult(v, m[0], m[4], m[8], m[3], m[1], m[5], m[9], m[10], ... mt11 = ml11 * mr11 + ml12 * mr21 + ml13 * mr31 + ml14 * mr41