量子领域的机器学习&人工智能（二）（Machine learning & artificial intelligence in the quantum domain）

原文作者：Vedran Dunjko；Hans J. Briegel
翻译者：Wendy

摘要（ Abstract）

  量子信息技术和只能学习系统都是新型的技术，它们很可能在未来对我们的社会产生变革性的影响。各个基础研究领域–量子信息（QI）与机器学习(ML)和人工智能（AI）–各自都有特定的问题和挑战，迄今为止，这些问题和挑战已被大量独立研究。然而，在最近的工作中，研究人员一直在探索这些领域在多大程度上可以真正相互学习和受益的问题。QML探索了量子计算与机器学习之间的相互作用，研究了如何将一个领域的结果和技术用于解决另一领域的问题。最近，我们见证了两个方面的重大突破。 例如，量子计算在加快机器学习问题的速度中找到了至关重要的应用，这对于“大数据”领域至关重要。相反，机器学习已经渗透到许多尖端技术中，并可能成为先进量子技术的重要工具。 除了数据分析中的量子加速或量子实验中使用的经典机器学习优化之外，理论上还证明了交互式学习任务的量子增强，突出了量子增强的学习代理的潜力。最后，探索将人工智能用于量子实验的设计以及自主进行部分真正研究的工作，报告了他们的首次成功。 除了相互增强的主题（探索ML / AI对量子物理学的作用，反之亦然）之外，研究人员还提出了学习和AI概念的量子概括的基本问题。 这涉及在量子力学充分描述的世界中学习和智力的意义的问题。 在这篇综述中，我们描述了在量子领域研究机器学习和人工智能的广泛研究中的主要思想和最新进展。

Ⅲ. 量子力学，ML和AI（QUANTUM MECHANICS, LEARNING, AND AI）

  量子力学对计算和信息处理领域产生了深远的影响。但是，直到最近，它对AI和学习的影响还是很小的。尽管ML和AI的领域与计算理论有很强的联系，但是这些领域仍然是不同的，并且（量子）计算中的所有进步都不意味着AI的质的进步。例如，尽管已经有20多年的历史了，但在量子计算方面最著名的还是Shor的因式 分解算法（Shor，1997），表面上看，它对AI没有影响。但是，其他不太知名的结果可能会应用于AI和学习的各个方面。因此，从早期开始，QIP领域就与AI的各个方面进行了详细而短暂的相互作用，尽管直到最近，这一研究领域才受到了广泛的关注。粗略地说，我们可以确定覆盖ML / AI之间相互作用的四个主要方向，如图10所示。

  从历史上讲，QIP与学习理论之间的第一个联系是根据量子理论直接应用统计学而形成的，这形成了第一条线：经典机器学习在量子理论中的应用以及本节中回顾的实验IV。在第一个主题中，机器学习技术被应用于来自量子实验的数据。相比之下，第二个主题是***基于真正的量子数据的机器学习***：在第五节中讨论的机器学习类型任务的量子泛化。这使我们进入了最近受到广泛关注的主题：量子计算机能真正地在以下方面提供帮助吗？机器学习问题，请参见第六节。我们将研究的最终主题考虑了QIP的各个方面，这些方面超出了机器学习（从狭义上讲），例如RL的概括，并且可以理解为通向量子AI的垫脚石。 VII.C节中对此进行了说明。

  值得一提的是，我们在这篇综述中讨论的综合领域有许多可能的自然分类。 我们选择的分类是基于对量子ML分类的两个不同观点的推动，这将在VII.B.1节中进一步讨论。

Ⅳ. 机器学习在量子物理中的应用（MACHINE LEARNING APPLIED TO (QUANTUM) PHYSICS）

  在本节中，我们将回顾直接使用ML方法或其他方法对QIP结果有用的工作和思想。 为此，我们面临着指定ML方法边界的艰巨任务。 近年来，部分由于机器学习在各个领域的成功，机器学习已成为一个理想的关键词，因此成为广泛技术的总称。 这包括用于解决真正学习问题的算法，还包括为间接相关问题设计的方法和技术。 从这种无所不包的角度来看，机器学习还包括（参数）统计学习，解决黑盒（或无导数）优化问题，以及解决一般性难题。

  由于我们不打算建立严格的界限，因此我们采用了更具包容性的观点。 对于QIP应用，可以想到的是，使用这种方法的所有作品的集合都可能适合ML，因此无法在一份评论中进行介绍。 因此，我们将重点放在开创性作品上，并在作者自己宣传二手方法论的ML风格的作品中加以强调，从而强调了此类ML / QIP跨学科研究的潜力。

  如前所述，在QIP中使用ML相当重要，最近几年相关作品取得了爆炸性的发展。 ML已被证明在许多与QIP相关的问题中有效：在 量子信号处理，量子计量，哈密顿估计以及量子控制问题 中。近年来，应用范围已得到显着扩展，机器学习和相关技术也已应用于在执行 量子计算，凝聚态和多体物理学中的问题以及新型量子设计中对抗噪声。光学实验。这样的结果表明，先进的ML / AI技术将在未来的量子实验室中发挥不可或缺的作用，尤其是在先进的量子设备以及最终的量子计算机的构造中。在一个互补的方向上，QIP应用程序也采用了许多ML方法，这表明QIP也可能成为前沿ML研究的有希望的试验场。

  统计学习理论（作为ML理论基础的一部分）与量子理论之间的联系自然而然地归因于量子理论的统计基础。量子信号处理的早期理论（Helstrom，1969），量子理论和量子态估计的概率方面（Holevo，1982）以及早期的工作（Braunstein and Caves，1994）都将导致现代量子计量学的发展（Giovannetti等）等（2011年）包括统计分析，为更高级的ML和QIP相互作用奠定了基础。相关的早期工作进一步强调了统计方法的适用性，特别是 最大似然估计对量子层析成像 方案的适用性， 例如状态估计的任务（Hradil，1997），量子过程的估计（Fiur´aˇsek和Hradil，2001）以及测量（Fiur´aˇsek，2001）和从不完整的层析成像数据重建量子过程（Ziman等，2005） 。这种类型的作品通常集中于可以应用纯分析理论的物理场景。但是，特别是在实验或嘈杂的（因此，现实的）设置中，许多对纯分析处理至关重要的假设都失败了。这导致我们考虑的针对QIP的ML应用的第一类。

A. 哈密顿估计和计量（ Hamiltonian estimation and metrology）

执行摘要：计量方案可能涉及 复杂的测量策略，例如，需要执行的测量可能取决于先前的结果。 此外，可以借助 附加参数（所谓的控件）来控制所分析的物理系统，这些参数可以顺序修改，从而导致更复杂的可能性空间。 机器学习技术可以帮助我们在各种约束条件下找到如此复杂的策略优化，这些约束条件通常是出于实用和实验目的的约束条件。

  识别物理系统的属性，无论是演化的动态属性（例如，过程层析成像），还是给定系统状态的特征（例如，状态层析成像），都是一项基本任务。 这些任务可以通过各种（经典的）计量理论和方法来解决，这些理论和方法可以确定最佳策略，表征误差范围，并且也已经普遍输出到量子领域。 例如，量子计量学研究 量子系统参数 的估计，并且通常确定用于其估计的最佳测量策略。 此外，量子计量学特别注重真实的量子现象（与复杂的，难以实现的量子装置的实现相关，甚至有时由其实现而定义的一种现象）相对于简单，经典策略而言具有优势的场景。

  通常，最佳策略的规范构成了计划的问题，为此可以采用各种机器学习技术。 查找测量策略的ML应用的第一个示例源自 相位估计 问题，这是哈密顿估计的一种特殊情况。 有趣的是，这种简单的情况已经为机器学习技术提供了丰硕的成果：分析上最佳的测量策略相对容易找到，但在实验上不可行。 反过来，如果我们限制为一组“简单的度量”，则可能会获得接近最佳的结果，但是它们需要困难地优化自适应策略，而ML是最适合的问题类型。 汉密尔顿估计问题也已在更一般的环境中得到解决，需要使用更复杂的设备。 我们首先简要介绍基本的汉密尔顿估计设置和计量概念。 然后，我们将结合ML和计量学问题来深入研究这些结果。

1. 哈密顿量估计（ Hamiltonian estimation）

哈密顿量：哈密顿量是一个物理词汇，是系统的能量算符，是一个 描述系统总能量的算符，以H表示。哈密顿量在大部分的量子理论公式中十分重要。H=T+V（其中T是动能，V是势能）。p=-ih∇ 是动量算子，其中∇是del运算符。 ∇自身的点积是拉普拉斯算子∇2。

  一般情况下，哈密顿量估计是量子域中计量学的一个常见实例，它考虑了一个由特定族H（θ）内（部分未知）哈密顿控制的量子系统，其中θ=（θ1，…，θn） 是一组参数θ。 粗略地说，哈密顿量估计处理确定用于估计哈密顿参数的最佳方法（及其性能）的任务。这相当于优化了初始状态（探针状态）的选择，该状态将在哈密顿量下演化，而后续测量的选择则揭示了哈密顿量具有的影响，从而间接地揭示了参数值。这个专业研究领域考虑了该任务的许多限制，变化和概括。例如，假设我们可以控制汉密尔顿演化时间t，或者将其固定为t = t0（通常分别称为频率和相位估计）的设置。此外，可以通过 多种方式来衡量过程的效率。在常用的方法中，人们主要对估算策略感兴趣，该策略粗略地说是允许根据测量次数对估算精度进行最佳缩放。感兴趣的数量是所谓的 量子费希尔信息，它 限制并量化缩放比例。凭直觉，在这种情况下，也称为本地制度，通常会假定许多重复的测量。在贝叶斯或单次使用的方案中，先验信息是中心对象（Jarzyna和Demkowicz），先验信息以待估计参数的分布形式给出，并根据测量策略和结果将其 更新为后验分布。 -Dobrzan´ski，2015年）。这里的目标是确定准备/测量策略，以最佳地减少后验分布的平均方差，该 后验分布是通过贝叶斯定理计算 的。

  可以说，这个问题的主要兴趣之一是，在探针状态和测量的结构中 利用真正的量子特征（例如纠缠，压缩等）可能会导致证明有效的估计， 这比许多所谓的自然估计问题的经典策略方法更为有效。 这种量子增强可能具有巨大的实际意义（Giovannetti等，2011）。 在某些“干净的”理论情景中已经实现了对最佳情景的识别，但是，这通常是不现实或不切实际的。 在这种情况下，机器学习支持的优化和其他机器学习方法可以提供帮助。

2. 相位估计设置（Phase estimation settings）

  从ML角度来看，有趣的估计问题已经可以在光学干涉仪相位移动的简单示例中找到，或者为平衡干涉仪的两个支路之一都包含θ的相移。 早期表明，给定最佳探针状态，平均光子数N和最佳（所谓的规范）测量，渐近相位不确定性可以衰减为N-1（Sanders和Milburn，1995），已知 作为海森堡极限。 相比之下，对“简单测量策略”的限制（如作者所述），仅涉及两个输出臂中的光子数测量，就可以达到√N-1的二次弱标度，称为 标准量子极限。这在更广泛的意义上得到了证明：最佳测量值无法通过输出臂的光子数量测量值的经典处理后来实现，而是构成了一个涉及实验上不可行的POVM（Berry和Wiseman，2000）。 但是，在（Berry和Wiseman，2000年）中，展示了如何使用“简单测量”来规避这一问题，前提是可以在运行时对其进行更改。 每次测量都包括输出臂的光子数测量，并由自由臂中φ的附加控制相位移动来参数化。同样，未知相位可以通过选定的φ进行调整。 最佳的测量过程是一种 自适应策略：准备一个纠缠的N光子状态（参见例如（Berry等，2001）），将光子顺序注入干涉仪中，并测量光子数。 在每个步骤，通过选择不同的相移来修改执行的测量，该相移取决于先前的测量结果。 在（Berry和Wiseman，2000； Berry等，2001）中，给出了一个明确的策略，该策略实现了最佳阶O（1 / N）的海森堡（Heisenberg）缩放。 但是，对于N> 4，表明该策略并非严格最优。

  这种类型的计划很困难，因为它减少了解决非凸优化问题。 机器学习领域也处理此类计划问题，为此目的开发了许多优化技术。 此类机器学习技术的应用，特别是粒子群优化，是在开创性工作（Hentschel和Sanders，2010，2011）以及后来的工作（Sergeevich和Bartlett，2012）中首次提出的。 在随后的工作中，也许已经证明了更著名的 差分进化方法 是更好的和更有效的计算方法（Lovett等，2013）。

3. 广义哈密顿量估计（Generalized Hamiltonian estimation settings）

哈密顿量 是所有粒子的动能的总和加上与系统相关的粒子的势能。 对于不同的情况或数量的粒子，哈密顿量是不同的，因为它包括粒子的动能之和以及对应于这种情况的势能函数。
哈密顿量的对角化 就是解一个本征值问题(在线性代数中就是特征值和特征向量)。对角化哈密顿量的过程就是一个找能量本征值的过程（找到这个系统可能存在的能量）。或者是一个去耦合的过程（比如说两个弹簧振子振动时存在耦合，可以写成一个哈密顿量的形式，对角化后，找到了弹簧振子的简振模，就去耦合了）
对角化的物理含义就是找到一个能量系统中的可能能量（一般来说这些能量都是分立的，这就是量子力学的精髓之一）
在势场V（x）中的粒子，其经典哈密顿量H=T+V的算符表示成 Hamilton算符=动能算符+势能，势能是与位置X相关的量，没有相应的算符表示，而动能算符表示为 （动量算符的平方/两倍的质量）。 动量算符的表达形式在计算自由粒子动量平均值的过程中通过自由粒子在坐标和动量表象下的波函数变换求出。具体的公式推导可以去看量子力学。
薛定谔方程的表达形式就是哈密顿量本征函数的形式。

  机器学习技术也可以用于量子过程估计的更一般的设置中。 更一般的汉密尔顿估计设置考虑由HC（θ）给出的部分受控演化，其中C是系统控制参数的集合。 这是一个合理的设置，例如 具有控制（C），但需要确认其实际性能（取决于θ）的量子组件的产出。此外，由于产出设置很少相同，因此通过允许仅对概率未知的参数θ进行特征化，甚至可以进一步概括该设置。 更准确地说，它们概率性地依赖于另一组超参数ζ=（ζ1，…，ζk），从而根据已知的条件概率分布P（θ|ζ）来确定分布参数θ。因此，当理解了噪声的影响（由P（θ|ζ）给出）时， 这种估计超参数ζ的通用任务可以处理具有固有随机噪声的系统。 依靠贝叶斯实验设计（BED）（Loredo，2004）的经典学习技术，结合Monte Carlo方法， 在（Granade et al，2012）中解决了这种非常普遍的情况。此方法的详细信息不在本文的讨论范围之内，但是，粗略地说，BED假设对上述类型的实验采用贝叶斯方法。 一般问题的估计方法（为简单起见，忽略超参数和噪声，尽管应用相同的技术）实现了条件概率分布P（d |θ; C），其中d对应于实验数据，即实验中收集的测量结果 。 假设在隐藏参数（P（θ））上有先验分布，则给定实验结果的后验分布通过贝叶斯决定：

上面的评估已经是不平凡的，主要是因为归一化因子P（d | C）包括对参数空间的积分。 此外，特别有趣的是多次重复实验的方案。 在这种情况下，类似于上面讨论的计量的自适应设置，根据结果调整控制参数C是有益的。

  BED（Loredo，2004年）通过为每个更新步骤选择后续控制参数C来最大化效用函数来应对此类自适应设置。 贝叶斯更新包括每个步骤的P（θ| d1，…，dl-1dk）∝ P（dk |θ）P（θ| d1，…，dl-1）的计算。 但是，归一化因子P（d | C）的评估也不是简单的，因为它包括对参数空间的积分。 在（Granade等人，2012）中，这种 积分是通过数值积分技术解决的，即顺序蒙特卡洛，产生了一种用于鲁棒哈密顿估计的新技术。

  后来，鲁棒的汉密尔顿估计方法 在使用对可信量子模拟器的访问中得到扩展，从而形成了一种更强大，更有效的估计方案（Wiebe等人，2014b），该方案也显示出对一般噪声和不完美缺陷的鲁棒性。（Wiebe 等人，2014c）、（Wang等人，2017）通过实验实现了使用模拟器进行估算的方法的受限版本。最近，与鲁棒的汉密尔顿估计方法联系在一起，基于贝叶斯方法和顺序蒙特卡洛的估计已进一步与粒子群优化技术相结合（Stenberg等人，2016）。其目标是在简单的解干系统中实现可靠的耦合强度和频率估计，这与实际的物理模型相对应。更具体地说，所研究的问题是Jaynes-Cummings模 型中场-原子耦合项和模频率项的估计 。控制参数是局部量子位强度，通过交换光谱法进行测量。

  除了使用ML对受控量子系统进行部分过程层析成像外，ML还可以帮助解决量子控制的真正问题，特别是目标量子门的设计。 这形成了后续主题。

B. 目标进化设计（Design of target evolutions）

执行摘要：量子信息的主要任务之一是 目标量子演化的设计，包括量子门设计。 可以通过量子控制解决这一任务，量子控制研究受控的物理系统，在系统演化过程中可以调整某些参数，或者使用扩展的系统和未调制的动力学。 在这里，潜在的问题是优化问题，即 寻找将被完全指定的系统的最佳控制功能或扩展系统参数的问题。 在现实的约束下，这些优化任务通常是非凸的，因此对于常规优化器而言很难，但仍适合高级ML技术。 目标进化设计问题也可以通过使用实际实验系统的反馈来解决，从而可以使用在线优化方法和RL。

  从QIP的角度来看，最重要的任务之一是设计量子计算所需的基本量子门。 量子控制是这种方法的范式，其目的是确定物理系统的控制领域需要如何及时调整以实现所需的发展。 目标进化的设计也可以在其他环境中实现，例如 通过使用 更大的系统 和 未调制的动态。 在这两种情况下，机器学习优化技术都可以用来设计最佳策略。 但是，通过与可调物理系统进行交互，也可以在运行时实现目标演变，而无需对系统进行完整描述。 我们首先考虑线下设置，然后在后面的在线设置中简短地评论一下。

1. 离线设计（Off-line design）

  量子控制中的范式设置考虑具有可控（c）和不可控部分（dr）（例如，H(C(t)) = Hdr + C(t)Hc）。自由部分通过（实值）控制场C（t）进行调制。在时间T限制下，最终时间积分算子U = U[C(t)] ∝ exp{−i∫T 0 dtH(C(t))}是所选场函数C(t)的函数。典型的目标是指定控制场函数C（t），该场函数使从某些初始状态| 0>到最终状态|φ>的转移概率最大化，因此找到argmaxC |<φ| U [C（t）] | 0> |。通常，映射C（t）→U [C（t）]涉及很多，但是从经验上来看，贪婪优化方法 提供了最佳解决方案（这是贪婪方法在实践中占主导地位的原因）。 后来从理论上阐明了这种经验性观察（Rabitz等人，2004），这表明在通用系统中不存在局部极小值，这导致易于优化（另请参见（Russell和Rabitz，2017年），以获取最新研究信息。）这对于实验来说是个好消息，但也表明量子控制不需要先进的ML技术。 但是，这种一般性要求通常所采用的那样，潜在的微妙假设是脆弱的，常常会被打破。 特别是，即使我们在控制维数和参数上仅放置相当合理的约束条件，即使在低维情况下，用于优化上述控制问题的贪婪算法也会失败。对于具有允许的演化时间t以及时间相关控制参数的线性化精度有约束条件的3层和2量子位系统，有可能构建贪婪方法失败而全局优化（无导数）方法尤其是差分进化成功的例子（Zahedinejad等，2014）。

  离线控制的另一个示例涉及高保真单发三量子位门的设计，该设计在（Zahedinejad等人，2015，2016）中使用一种专门的新颖优化算法进行了处理，作者将其称为子 空间选择性自优化算法，自适应差分进化方法（SuSSADE）。 门设计的一种有趣的替代方法是利用大型系统。 经过专门设计的大型系统可以自然地在子系统上实现所需的演化，而无需依赖时间的控制（参见具有始终在线交互的QC（Benjamin和Bose，2003））。 换句话说，尽管全局动态未调制，也实现了局部门。 对于离线设计门而言，构建这样的全局动力学的一项重要任务是（Banchi等人，2016年）通过一种依靠随机梯度下降的方法来解决，并借鉴了监督学习技术。

2. 在线设计（ On-line design）

  作为离线方法的补充，这里我们假设可以进行实际的量子实验，而 最佳策略的确定则依赖于在线反馈。 在这些情况下，无需事先完全指定量子实验。 此外，所需的方法倾向于在线计划和RL，而不是优化。 在需要优化的情况下，由于实验的限制，优化的参数是不同的，请参阅（Shir等人，2012）以获取对该主题的更详细了解。

  在早期的工作中，使用实验反馈将系统“引导”到期望的进化的在线方法之间的联系已经与机器学习相联系（Bang等，2008； Gammelmark和lmer，2009）。这些探索性工作通过实验反馈来解决通用控制问题，尤其是在当时，社区几乎没有注意到这些探索性工作。在最近的时间里，基于反馈的学习和优化 受到了越来越多的关注。例如，在（Chen等人，2014）中，作者探索了改进的Q学习算法对RL的经典控制问题的适用性（见II.C节）。此外，在（Palittapongarnpim 等人，2016）中，已经在最佳参数估计的背景下讨论了RL方法的潜力，但也讨论了典型的最佳控制场景。在后面的工作中，作者还提供了一个简短而又广泛的相关主题概述，简述了一种解决量子测量和控制难题的方法，该观点统一了ML和RL的各个方面。在（Clausen and Briegel，2016）中，在一般控制和反馈问题的背景下对基于PS更新的RL进行了分析。最后，先前在（Machnes 等人，2011）中提供了统一的量子控制计算平台的想法，尽管没有明确强调ML技术。

  在下一节中，我们将进一步简单地介绍了我们的观点，并考虑机器学习技术控制各种门和更复杂过程的场景，甚至帮助我们学习如何进行有趣的实验。

C. 控制量子实验和机器辅助研究（Controlling quantum experiments, and machine-assisted research）

执行摘要：ML和RL技术可以帮助我们控制复杂的量子系统，设备，甚至量子实验室。 此外，它们作为副产品也可以帮助我们进一步了解实验中研究的物理系统和过程。 如自适应控制系统（代理），该系统学习如何控制量子装置，如电子装置。 如何保存量子计算机的内存，如何处理噪声过程，生成纠缠的量子态以及如何关注目标进化。 在学习这种最佳行为的过程中，甚至简单的人工代理也以隐含的体现，理解的方式学习了有关底层物理的知识，我们可以使用这些物理知识来获得新颖的见解。 换句话说，人工学习代理可以真正帮助我们进行研究。

  目前已经研究了对于量子实验这种高级实验设计中使用ML和AI的前景。 在这里，人们考虑了控制复杂过程的自动化机器，例如 指定执行更长的简单门序列或执行量子计算。 此外，有人建议 将学习机用于量子实验的设计中，并与之集成在一起，从而帮助我们进行真正的研究。 我们首先给出两个结果，其中ML和RL方法已被用于控制更复杂的过程（例如，生成量子门序列以保留内存），并考虑了机器的观点，这些观点将在以后真正地帮助研究。

1. 控制复杂流程（Controlling complex processes）

  用于生成对稍微复杂的系统的控制的所涉及的机器学习机器的最简单示例是在 量子内存的动态解耦问题 中完成的。 在这种情况下，将量子存储器建模为与耦合的系统（系统具有局部哈密顿量（HS）和浴HB），并且通过耦合项HSB实现解干。 HS捕获了本地单一错误。哈密顿总噪声= HS + HB + HSB的演变将破坏内存的内容，但是可以通过添加仅对系统起作用的可控局部项HC来缓解这种情况。控制哈密顿量HC的某些最佳选择是已知的。 例如，我们可以考虑以下情形：对HC进行调制，使其以间隔Δt顺序执行瞬时Pauli-X和Pauli-Y ary运算。由于该间隔（也是引起退相干的自由演化的时间）接近零，因此∆t→0，因此可以确保完美记忆。 但是，一旦使设置更加实际，允许有限的Δt时间，最佳序列的空间就会变得复杂。 特别是，最佳序列的开始取决于∆t，噪声哈密顿量的形式以及总演化时间。

  为了确定最佳序列，在（August和Ni，2017）中，作者采用了 循环神经网络，将其作为生成模型进行训练，这意味着他们经过训练可以产生使最终噪声最小化的序列。 网络生成的整个脉冲序列（保利门）表现出优于众所周知的序列。

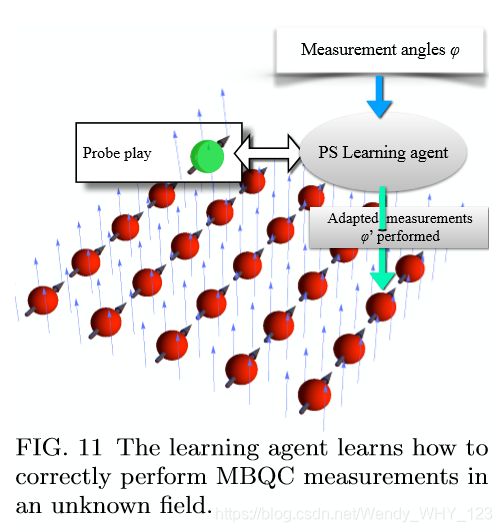
  在本质上不同的环境中，必须发生相互作用，作者研究了如何使用AI / ML技术使量子协议本身具有适应性。 特别是，作者将基于PS的RL方法（Briegel和De las Cuevas，2012）（见VII.A节）应用于 保护量子计算不受局部杂散场影响的任务（Tiersch等，2015）。在MBQC中（Raussendorf and Briegel，2001; Briegel 等人，2009），计算是通过对较大的纠缠资源状态（例如簇状态）执行自适应单量子位投影测量来驱动的（Raussendorf和Briegel，2001）。在资源状态暴露于杂散场的情况下，每个量子位都会经历局部旋转。为了减轻这种情况，作者在（Tiersch 等人，2015）中引入了学习代理，该代理“玩”一个本地探针量子位，并以σx的+1本征状态初始化，表示为| + i，学习如何补偿未知领域。本质上，给定度量，代理选择不同的度量，只要观察到+1结果，便获得奖励。因此，对代理进行了训练以补偿未知字段，并充当所需测量值与应在给定设置（即在给定字段中以给定测量频率（∆t）执行的测量）之间的“解释器”，参见图11。缓解此类固定杂散场的问题自然可以通过非自适应方法解决，在这种方法中，我们使用有关系统的知识来解决问题，例如测量领域并据此进行调整，或使用容错结构。

从学习的角度来看，这种直接方法有一些缺点，出于教学目的可能值得提出。容错方法显然是浪费的，因为它们无法利用任何有关噪声过程的知识。相反，领域估计方法学得太多，并假设一个世界模型。为了澄清后者，以补偿测得的场，我们需要使用量子力学，特别是伯恩定律。相反，RL方法是无模型的：Born规则不起作用，“正确行为”是可以学习的，并且仅根据经验来确定。这在概念上是不同的，但在操作上也很关键，因为无模型方法可实现更大的自治性和灵活性（即，同一机器可在更多环境下使用而无需干预）。关于学习过多，统计学习的基本原理之一是“当解决感兴趣的问题时，不应将更一般的问题作为中间步骤来解决”（Vapnik，1995），这很直观。提出的设置的问题是“如何调整测量设置”，而不是“表征杂散场”。虽然在当前情况下，两个问题的信息理论内容可能是相同的，但不难想象，如果考虑到更复杂的领域，则完整的过程表征所包含的信息远远多于优化局部测量所需的信息。 （Tiersch等人，2015）的方法可以进一步推广，以利用稳定剂测量中的信息（Orsucci等人，2016），或者类似地使用编码时的综合症测量结果（Combes等人，2014），（而不是探针状态）。为了解决一些相关问题，（Mavadia等人，2017）中的作者使用有监督的学习方法，也展示了如何在实验中补偿量子比特的不连贯性（随机演化）。

2. 学习实验（learning how to experiment）

  RL在QIP中应用的第一个例子出现在实验光子学的背景下，其中当前的挑战之一是 产生高度纠缠的高维多方态。 此类状态在光学平台上生成，其配置为生成复杂的量子态可能是违反直觉的且是非系统的。 可以将有趣的搜索配置映射到RL问题，只要学习代理生成有趣的状态（在模拟中），就会获得奖励。 在前体研究中（Krenn等人，2016），作者使用 反馈辅助搜索算法 来识别先前未知的配置，这些配置会 生成新颖的高度纠缠态。 这表明新颖的量子实验的设计也可以实现自动化，从而可以极大地促进研究。在光学平台的背景下给出的这个想法随后与早期的提议相结合，即在量子信息协议中使用AI代理，并在未来的量子实验室中将其作为“实验室机器人”（Briegel，2013年）。这导致基于PS框架的更先进的RL技术的应用，用于了解可通过光学平台访问的希尔伯特空间以及自主机器发现有用光学设备的任务（Melnikov等，2017）。与从实验机中学习新见解的主题相关，在（Bukov等人，2017）中，作者考虑了通过选择脉冲（实施旋转限制）来准备目标状态的问题。这是一项标准的控制任务，作者表明RL取得了可观的，有时甚至接近最佳的结果。但是，就我们的目的而言，这项工作最相关的方面涉及以下事实：作者还说明了ML / RL技术如何通过规避人类的直觉而可用于在量子实验和非平衡物理学中获得新的见解。可以被冻结。有趣的是，作者们也证明了相反的观点，即物理学见解如何帮助阐明学习问题。

B. 凝聚态和多体物理学中的机器学习（Machine learning in condensed-matter and many-body physics）

执行摘要：多体物理学的典型问题之一是 物质相的识别。 机器学习和物理学的这一分支之间的普遍重叠表明，可以训练有监督和无监督的系统来对不同的阶段进行分类。 更有趣的是，无监督学习可用于检测阶段，甚至发现顺序参数-可能真正导致新颖的物理见解。 另一个重要的重叠部分是 考虑（广义）神经网络的表征能力，以表征有趣的量子系统族。 两者都建议一方面的某些学习模型与另一方面的物理系统之间存在更深的联系，其范围是目前重要的研究主题。

  在过去的20年中，机器学习技术已成为处理高度复杂系统的许多自然科学必不可少的工具。这些包括生物学（特别是遗传学，基因组学，蛋白质组学和计算生物学的一般领域）（Libbrecht和Noble，2015年），医学（例如流行病学，疾病发展等）（Cleophas和Zwinderman，2015年），化学（Cartwright） （2007年），高能与粒子物理学（Castelvecchi，2015年）。毫不奇怪，它们还渗透到凝聚态物质和多体物理学的各个方面。在量子力学和密度泛函理论的背景下（Curtarolo等人，2003； Snyder等人，2012； Rupp等人，2012； Li等人，2015a）提出了这种方法的早期实例，或者用于近似计算。单点安德森杂质模型的格林函数（Arsenault等，2014）。从那以后，人们对神经网络与多体和凝聚态物理之间的联系的兴趣得到了极大的发展。接下来我们将讨论的一些结果与本综述的主要主题不同，这些结果与QIP和ML的重叠有关。但是，由于QIP，凝聚态物质和多体物理学有明显的重叠，因此我们认为至少要充实基本概念很重要。

  该领域的基本研究之一涉及 物质相的学习以及物理系统中相变的检测。一个典型的例子是对来自不同物质阶段的构象样本的辨别。低于或高于临界温度的热状态的伊辛模型配置。使用主成分分析和最近邻无监督学习技术已经解决了这个问题（Wang，2016）（另请参见（Hu et al。，2017））。这样的方法不仅具有检测相位的潜力，还具有实际 识别阶跃参数 的潜力（Wang，2016年）–在上述情况下。更复杂的问题是磁化强度，例如区分 库仑相 的方法已使用基本的前馈网络解决，并且对卷积神经网络进行了训练，以检测 拓扑相 （Carrasquilla和Melko，2017年），而且还检测了 立方晶格上的费米离子系统中的相（Ch’ng等人，2016年） ）。神经网络也已与量子蒙特卡洛方法（Broecker等，2016）和无监督方法（van Nieuwenburg等，2017）（也应用于（Wang，2016））相结合，在两种情况下均能改善分类在各种系统中的性能。值得注意的是，在没有系统哈密顿量的任何信息的情况下，所有这些方法在“学习”阶段都非常成功。虽然该领域的重点主要放在神经网络架构上，但其他受监督的方法，特定的内核方法（例如SVM）已用于相同的目的（Ponte和Melko，2017年）。内核方法在某些情况下可能是有利的，因为它们可以具有更高的可解释性：在内核方法而不是NN的情况下，通常更容易理解最优模型的原因，这也意味着对基础物理学的了解可能是在内核方法的情况下更容易。请注意，在未来的几年中，这很可能会受到深度NN方法的挑战。

  神经网络方法对物质阶段进行分类的成功背后的部分解释可能在于它们的形式。特别地，它们在经典的量子情况下都可能具有编码物理系统重要属性的能力。这激发了我们在这种情况下提到的第二条研究路线。 玻尔兹曼机（BM），即使是其受限变体，也已知***具有编码复杂分布***的能力。从同样的意义上讲，受限的BM扩展为接受复杂的权重（即等式（2）和（3）中的权重wij）编码量子态，并且隐藏层捕获经典和量子（纠缠）相关性。在（Carleo and Troyer，2017）中证明了这种方法准确地描述了许多原型系统的平衡和动力学特性：也就是说， 受限制的BM形成了有用的量子态，称为有趣的量子态（称为神经网络量子态（NQS）） ，隐藏层中神经元的数量控制希尔伯特空间可表示子集的大小。例如，这类似于键的大小如何控制拟定矩阵积状态的范围（Verstraete等，2008）。为了实现有效的量子态断层扫描，也可以利用该特性（Torlai等人，2017）。在随后的工作中，作者还分析了NQS状态的纠缠结构（Deng等人，2017），并提供了深度受限BM表示能力的分析证据，证明它们可以例如表示具有多项式大小差距的任何k局部哈密顿量的基态（Gao and Duan，2017）。值得注意的是，标准变分表示的表示能力（例如变分重整化组的表示能力）已与深层神经网络（Mehta and Schwab，2014）形成对比，目的是阐明深层网络的成功之处。与此相关的是，张量网络（Ostlund and Rommer，1995; Verstraete and Cirac，2004）形式主义已被用于深度卷积算法电路的有效描述，还在量子多体态与深度学习之间建立了正式的联系（ Levine等人，2017）。最近，机器学习与多体量子物理学之间的交汇也启发了对机器学习动机的纠缠证人和分类器的研究（Ma and Yung，2017; Lu et al。，2017），并且进一步促进了机器学习与许多量子力学之间的联系。物理，特别是 量子纠缠理论。这些最新结果将神经网络定位为在凝聚态物理和多体物理环境中应用的最令人兴奋的新技术之一。此外，它们还显示了影响力反方向的潜力–多体物理学的数学形式主义在加深我们对复杂学习模型的理解中的应用。

Ⅴ. 机器学习概念的量子广义化（ QUANTUM GENERALIZATIONS OF MACHINE LEARNING CONCEPTS）

  量子理论的兴起改变了我们对物理系统的描述方式，也需要改变我们对信息是什么的理解。量子信息是一个更宽泛的概念，QIP利用真正的量子特征进行更有效的处理（使用量子计算机）和更有效的通信。这种典型的量子性质，例如甚至纯状态也无法完美复制的事实（Wootters和Zurek，1982），经常被认为是许多量子应用（如密码学）的核心。同样，典型的信息处理操作在量子世界中更为普遍：封闭的量子系统可以经历任意单元的演化，而相应的经典封闭系统演化对应于（有限）排列组。大部分机器学习文献都涉及到数据的学习，即经典信息。本节研究当数据（可能是其处理过程）从根本上来说是量子时，ML看起来像什么的问题。我们将首先探讨监督学习的量子概况，其中“数据点”真正的量子态。这会产生大量在经典情况下无法区分的场景（例如，具有相同示例的一个或两个副本是不一样的！）。接下来，我们将考虑另一种学习的量子泛化，其中量子态用于表示CLT中未知概念的泛化-因此，我们谈论量子态的学习。接下来，我们将介绍一些有关POMDP的量子概括的结果，这可能会导致量子广义的强化学习（尽管这实际上只是概括了数学结构）。

A. 量子概括：量子数据的机器学习（ Quantum generalizations: machine learning of quantum data）

执行摘要：机器学习领域的重要部分涉及数据分析，分类，聚类等。QIP概括了标准数据概念，包括量子态。 量子信息的处理受到限制（例如，不克隆或不删除），但也带来了新的处理选项。 本节讨论如何将常规ML概念扩展到量子域的问题，主要集中在量子系统的监督学习和可学习性方面，以及RL基础。

  机器学习的基本问题之一是监督学习，其中训练集D = {{（xi，yi）} i用于推断将数据点映射到标签xi rule→yi的标记规则（更多信息，请参阅IB部分） ）。 更一般而言，监督学习处理经典数据的分类。 在QIP中，数据是量子化的-也就是说，所有量子状态都承载或表示（量子）信息。 使用{（ρi，yi）} i类型的数据集可以做些什么，其中ρi是一个量子态。 通常说来，经典数据和量子数据之间的关键区别之一是 量子数据不能被复制。 换句话说，用符号（ρi⊗yi）表示的一个实例通常不如具有两个副本（ρi⊗yi）⊗2有用。相比之下，使用功能标签规则进行分类的情况是相同的。处理量子数据的最接近的经典模拟是 标记不是确定性 的或 条件分布P（label | datapoint）不是极值（Dirac） 的情况。这是对随机变量或概率概念进行分类（或学习）的情况，其中的任务是产生最佳猜测标签，并指定“最可能”产生数据点的随机过程。在这种情况下，可以在训练阶段访问从同一分布中独立采样的两个示例，这与拥有一个相同样本的两个副本和同一样本完全不同，它们完全相关且不包含任何新信息。为了获得有关分布或随机变量的完整信息，原则上需要无限多个样本。类似地，在量子情况下，无限地具有相同量子状态ρ的多个副本在操作上等同于具有给定状态的经典描述。

  尽管有相似之处，但量子信息仍然与纯粹的随机数据有所不同。 可以在量子态判别理论中确定ML类型分类任务的先驱，我们首先对此进行简要评述。 接下来，我们回顾一些涉及“量子模式匹配”的早期著作，该著作涵盖了有监督设置的各种类型，并且第一篇著作明确提出了对量子广义机器学习的研究。 接下来，我们讨论更一般的结果，这些结果表征了 量子环境中的归纳学习。 最后，我们介绍了有关使用量子数据学习的CLT观点，该观点解决了 量子态的可学习性。

1. 量子数据的状态区分，状态分类和机器学习（ State discrimination, state classification, and machine learning of quantum data）

  a. 状态区分（a. State discrimination ） 这个话题的切入点可以再次追溯到Helstrom和Holevo的开创性著作（Helstrom，1969； Holevo，1982），因为状态区分问题可以改写为监督学习问题的变体。 在典型的状态判别条件下，任务是确定给定的量子状态（作为在该状态下准备好的量子系统的一个实例），并保证它属于一个（通常是有限的）集合{ρi} i，其中 该集合是完全经典指定的。 回想一下，相比之下，状态估计通常假设连续的参数化族，而任务是参数的估计。 从这个意义上讲，状态区分是一个 离散的估计 问题，在整个QIP的历史中，一直在广泛和连续地考虑 识别最优度量（在各种优缺点下）和 最佳界限 的问题（Helstrom，1969； Croke等， 2008; Slussarenko等人，2017）。

  备注（Remark:） 传统的量子态判别可以改写为量子态的退化监督学习环境。 这里，“数据点”的空间限于有限的（或参数化的）族{ρi} i，并且训练集包含有效的有限数量的示例D = {（（ρi，i）⊗∞}; 自然地，该表示法只是对量子态进行完整经典描述的简写。在下文中，我们有时会写 ρ⊗∞来表示包含密度矩阵ρ的经典描述的量子系统。

  b. 量子模板匹配——经典模板（Quantum template matching – classical templates ) 分类或任务分配的一种变体是“模板匹配”（Sasaki 等人，2001），这是与ML和分类问题建立明确联系的首批作品之一。在这项开创性工作中，作者考虑了分类问题，其中输入状态ψ可能不对应（已知）模板状态{ρi} i，正确的匹配标签由最大的Uhlmann保真度确定。更准确地说， 任务定义如下：给定经典指定的模板状态族{ρi} i，给定M个量子输入ψ⊗M副本，输出用icorr =argmaxiTr[hp√ψρi√ψi]²定义的标记icorr。 在这项原始工作中，作者将重点放在具有纯状态输入的两类情况下，并确定此问题的完全量子和半经典策略。 “全量子策略”确定最佳的POVM。半经典策略将测量策略限制为可分离的测量，或对输入执行状态估计（一种“量子特征提取”）。

   c. 量子模板匹配–量子模板（Quantum template matching – quantum templates） 在（Sasaki等人，2001）的工作中，（Sasaki和Carlini，2002）的作者考虑了这样一种情况：我们没有获得经典模板状态{ρi} i的描述，而是得到了访问一定数量的K副本。换句话说，我们可以访问状态为Niρ⊗Ki的量子系统。设置K→∞，可以用经典模板进行复现。这种普遍的设置引入了许多复杂性，在使用经典模板的“更经典”情况下不存在这种复杂性。例如，对测量进行分类现在必须“用完”模板状态的副本，因为它们也无法克隆。作者确定了针对该问题的各种半经典策略。例如，如果模板状态是第一个估计的，我们将面临经典模板的情况（尽管有错误）。经典模板设置本身允许半经典策略，其中首先估计所有系统，并且允许相关策略。作者找到了K = 1的最优解，并证明存在严格优于直接半经典扩展的完全量子过程。

  备注（Remark）: 量子模板匹配问题可以理解为量子广义监督学习，其中训练集的形式为{（ρ⊗Ki，i）i}，训练集之外的数据来自⊗ψM族（副本数 是已知的），并且通过Uhlmann保真度测量得出的 最小距离来定义类别。 K→∞的情况接近经典模板的特殊情况。 将状态ψ限制为模板状态集（受限制的模板匹配），并将M设置为1可恢复标准状态判别。

   d. （受限）模板匹配的其他已知最优结果（Other known optimality results for (restricted) template matching ） 对于有限匹配的情况，保证输入来自模板集，在（Bergou和Hillery，2005年）中找到了两类设置的最佳解决方案，达到最小错误指数和统一先验输入。（Hayashi 等人，2005）。在（Hayashi等人，2006年）中，作者找到了明确判别情况的最佳解决方案。 对于任意先验，渐进最优策略限制了与有限模板K <∞的匹配，后来在（Gu¸ta˘and Kotl owski，2010）中发现了 混合量子位状态。这项工作还对相关主题进行了详细的介绍，回顾了用于统计学习的量子类比，并强调了与ML方法和概念的联系。

  后来，在（Sent´ss等，2012）中，作者介绍了这三种策略，并将它们与有限模板匹配的情况进行了比较：经典估计和区分，经典最优和量子策略。回想一下，这里的形容词“经典”表示训练状态在第一步就被完全测出了，量子集被转换为经典信息，这意味着不再需要量子记忆，并且可以实现真正的归纳学习。令人惊讶的结果是，直观的估计和区分策略将监督分类错误率降低为最优估计，再加上（标准）量子状态鉴别问题，并不是学习的最佳选择。另一种测量不仅可以提供更好的性能，而且 可以精确匹配最佳量子策略（相对于渐近而言） 。有趣的是，（Gu¸t˘a和Kot lowski，2010）和（Sent´ss等，2012）的结果对基本相同的设置提出了相反的主张：无分离，相干（完全量子）和半分离 -经典策略。这种 差异是由所选优绩指标的差异以及渐近最优性的不同定义引起的（Sent´s，2017年），有效地提醒了量子学习的微妙本质。随后，还在其他环境中探索了最佳策略。 当数据集包含相干状态时（Sent´ss等人，2015），或者在误差容限处于其他明确设置的情况下（Sent´ıs等人，2013）。

备注：电子向右自旋和正电子向左自旋的状态是相关联的，这一现象称作 量子相干性 。这种相干性只有用量子理论才能说明。
在量子力学里，当几个粒子在彼此相互作用后，由于各个粒子所拥有的特性已综合成为整体性质，无法单独描述各个粒子的性质，只能描述整体系统的性质，则称这现象为量子缠结或 量子纠缠（quantum entanglement）。量子纠缠是一种纯粹发生于量子系统的现象；在经典力学里，找不到类似的现象。
在量子力学里，开放量子系统的量子相干性会因为与外在环境发生量子纠缠而随着时间逐渐丧失，这效应称为 量子退相干（英语：Quantum decoherence），又称为量子去相干。

  e. 无监督学习的量子概括（Quantum generalizations of (un)supervised learning） 前面的作品考虑了 有监督学习问题的特殊归纳。 但是，第一次尝试从更广泛的角度对ML在量子世界中的外观进行分类和表征，这是在（Aèmeuret等人，2006）中进行的第一次明确尝试。在那里，引入的基本对象是标记的量子或经典对象的数据库，即DK n = {（|ψi>⊗i，yi）} n i = 1 ，它可以是副本。 通常可以使用经典或量子处理来处理这样的数据库以解决各种类型的任务。作者建议用表示为L（上下文，目标）的类来描述量子学习方案。 这里的上下文可能表示我们正在处理经典数据或量子数据，以及学习算法是否依赖于量子能力。 目标指定了学习任务或目标（也许是非常广泛的术语）。示例包括与标准经典ML相对应的L(c ,c)和L(q, c)，这可能意味着我们使用量子计算机来分析经典数据。本节前面考虑的模板匹配经典模板（K =∞）（Sasaki et al。，2001）的示例将表示为L(c, q)，而有限模板号K <∞的推广将在L(⊗K,)q中进行拟合。尽管以上形式主义建议重点关注有监督的设置，但作者还建议将数据集作为（无监督）聚类的输入。作者进一步研究了确定量子态紧密度的量子算法，这可能是量子聚类算法的基本构建块，并且还利用著名的Helstrom结果（Helstrom，1969）计算了特殊分类（状态区分）的某些误差范围。 ）。 （Lu and Braunstein，2014）使用了类似的想法来定义 用于量子状态下数据分类的量子决策树算法。

  在（Aèmeur等人，2006）中勾勒出的量子广义学习理论与在Helstrom中的经典理论（Helstrom，1969）之间的紧密联系在（Gambs，2008）中得到了更深入的探索。 作者在那里计算了解决几种类型的分类问题所需的样本复杂度的下限（在这种情况下，最小份数为K）。为此，作者介绍了一些将ML类型分类问题减少到可以直接应用理论的地方的技术（Helstrom，1969）。 这些类型的结果有助于在ML问题和QIP技术之间建立更深的联系。

  f.量子归纳学习（ Quantum inductive learning ） 归纳理论，渴望的学习会产生最佳的猜测分类器，该分类器可以根据训练集应用于数据点的整个域。但是，已经在关于经典模板与量子模板匹配的段落中讨论的结果（Sasaki和Carlini，2002）已经指出了该概念在量子领域中的问题–最佳分类器可能需要一个量子数据点的无限副本来进行分类。但这在量子领域似乎是禁止使用的。
近年来，从广义的角度探讨了以归纳形式对这种监督学习进行量子泛化的观点（Monr等人。，2017）。归纳学习算法在直观上仅使用训练集来指定假设（真实标记函数的估计）。相反，在转导推理学习中，还向学习者提供 无标签的数据点。这些未标记的点可能对应于交叉验证测试集或实际目标数据。即使标签是未知的，它们也会携带完整数据集的其他信息，这有助于识别正确的标签规则。另一个区别是，转导算法只需要标记给定点，而归纳算法则需要指定分类器，即 标记功能，定义在可能的点的整个空间上。在（Monr`as等人，2017）中，作者注意到算法的归纳属性对应于无标签属性，通过该属性，他们可以证明“归纳”（即“无信号传递”）是 等效于拥有仅根据训练集输出分类器h的算法，然后将其应用于每个训练实例。归纳学习的第三个等效特征是，训练和测试完全分为两个不同阶段。尽管这些观察在经典情况下是非常直观的，但实际上在量子世界中是有问题的。具体来说，如果训练示例是量子对象，则通常，量子无克隆属性会任意多次禁止使用假设函数（候选标记函数）。这很容易理解，因为如果我们要处理学习算法，则h的每个实例都必须以某种特殊的方式依赖于量子数据。 h的多个副本将需要量子数据（至少部分）的多个副本。

  可能的含义是，在量子领域中，归纳学习不能明确地分为训练和测试。 尽管如此，作者们表明，对于某些对称的绩效衡量标准，无信号标准意味着渐近地分离是可能的。 具体而言，对于任何量子感应无信号传递算法A，都存在另一种可能不同的算法A’，它在训练和测试阶段确实分开，并且渐近地实现了相同的性能（Monr`as等人，2017年）。 ）。 这种A’算法本质上利用了半经典策略。 换句话说，对于归纳环境，尽管无定理，经典直觉仍然存在。

2. 计算学习观点：量子态作为概念（ Computational learning perspectives: quantum states as concepts）

  前面的小节基于量子数据库示例，讨论了量子态的分类主题。 但是，整个理论基于存在一个标记规则，该规则会生成一类示例的假设，即并且机器可以学到标记规则。 此规则在CLT中也称为概念（例如PAC学习，有关详细信息，请参见II.B.1节）。一个合理的充分标准是，可以预测在此状态下进行任何两次结果测量的结果的概率，因为这已经可以进行完整的层析成像重建。从这个角度来看，“学习量子态”意味着什么？ “知道量子态”是什么意思？ 一个自然的标准是，如果可以预测任何给定测量的测量结果概率，则“知道”一种量子态。 在（Aaronson，2007年）中，作者从上述意义上解决了量子态的可学习性问题，其中概念的作用是由给定的量子态扮演的，“知道”这个概念就等于可以预测 给定度量的结果概率及其结果。与II.B.1中讨论的常规CLT的直接区别是，概念范围不再是二进制的。 然而，正如我们所证明的那样，经典的CLT理论具有连续范围的概括。特别地，所谓的p概念的范围在[0,1]（Kearns和Schapire，1994），并且存在与VC维类似的量以及与p概念相关的与泛化性能相关的类似定理。 案例（见（Aaronson，2007））。明确地说，这种广义理论的基本要素是：概念X的域，样本x∈X和p概念f：X→[0,1]。 这些抽象对象按如下方式映射到量子信息论的中心对象（Aaronson，2007年）：概念的域是两次量子测量结果的集合，而样本是POVM元素（简而言之：x↔Π） ; 要学习的p概念是量子状态ψ，并且对样本的概念/假设的评估对应于当状态ψ为时观察与Π相关的测量结果的概率Tr [Πψ]∈[0,1]。

  为了将基于数据分类的监督学习观点与上述CLT观点联系起来，请注意，在给定的量子态CLT中，该框架根据对概率的测量，将量子概念–量子态–“分类”了量子POVM元素（效应）。 观察这种效果。 该模型的训练集元素的形式为（Π，Tr（ρΠ）），且0≤Π≤1。按照CLT的精神，据说对于两个结果的广义测量元素（Π），在一定的分布D下，概念类“量子态”是可以学习的，如果对于每个概念-量子态ρ-都有一种算法可以访问 形式（Π，Tr（ρΠ））的示例，其中根据D绘制Π，当从D绘制Π0时，输出假设h（近似）正确地以高概率正确预测标签Tr（ρΠ0）。 假设在这里的假设可以简单地通过量子状态ρ的“最佳预测”经典描述来发挥。（Aaronson，2007）的主要结果是，仅在量子位的数量上（即在密度矩阵的维度上对数地）线性地缩放样本复杂度即可学习量子态。用可操作的术语来说，如果爱丽丝希望向将在其上执行两次结果测量的鲍勃发送n量子比特的量子状态（而爱丽丝不知道哪一个），则她可以通过发送（O（n））来达到近乎理想的性能。经典量子位，具有明显的实践意义和理论意义。从某种意义上讲，这些结果也可以被认为是霍夫沃定理的广义变体（Holevo，1982），限制了在量子系统的情况下可以存储和检索多少信息。到目前为止，尽管这是量子学习理论中的一项基本结果，但在层析成像方面，后一种结果比量子机器学习更具影响力。但是，出于完全实际的目的。以上结果带有警告。量子态的学习在样本复杂度上是有效的（例如，一个人需要执行的测量次数），但是，假设的重建的计算复杂度实际上在量子位数上是指数级的。最近，（Rocchetto，2017）也显示了用于学习稳定器状态的重构算法的效率。

B. （量子）学习与量子过程（ (Quantum) learning and quantum processes）

执行摘要：量子学习的概念已在文献中用于指代“学习”量子系统各个方面的研究。除了学习量子态，还可以考虑学习量子演化。在这里，“知道”在操作上被定义为有能力在以后的时刻实现给定的单位——–这类似于计算学习理论中的“已知”意味着我们可以在以后应用概念函数。最后，由于学习与在交互环境（RL）中的学习有关，因此可以考虑这种设置的量子概括。该方向上的第一个结果是对 POMDP的量子概括。请注意，由于POMDP构成RL的数学基础，因此，量子广义数学对象–量子POMDP可以构成量子广义RL的基础。

  a.学习量子过程（ Learning of quantum processes） 学习的概念是非常分散的，“量子学习”在研究中被经常使用，并且并非每个实例都对应于机器或统计学习意义上的“经典学习”的概括。尽管如此，一些这样的著作进一步说明了人们在学习经典或量子物体的同时可以使用经典（量子）工具所采用的方法之间的区别。

  *学习单元（Learning unitaries ）*例如，“ 单位运算的量子学习”已用于指代未知单元运算的最佳存储和检索任务，该过程分为两个阶段。 在 存储阶段，可以访问某个统一单元U的几种用法。在 检索阶段，给定一个（或几个完全未知的）状态|ψ>的一个或几个实例，要求人们近似状态U |ψ>。 像量子模板状态（请参阅第VA1节）一样，我们可以区分半经典的准备和测量策略（其中U被估计并表示为经典信息），以及量子策略，其中这个应用于某些 资源状态，它在检索阶段与输入状态|ψ>一起使用。最佳策略问题没有简单的普遍答案。在（Bisio等人，2010）中，作者表明，在合理的假设下，令人惊讶的结果是 最优策略是半经典的。相比之下，在（Bisio 等人，2011）中，对通用测量提出了相同的问题，而事实却恰恰相反：最优策略需要量子记忆。参见例如 （Sedla等人。，2017）获得有关概率单元存储和检索的一些最新结果，这可以理解为真正的量子操作量子学习。

  学习测量(Learning measurements ) 首先，要确定面对哪个测量设备的问题是相对较少的工作，请参见 （Sedlak和Ziman，2014年）。 与此相关的是，我们在学习度量的主题上遇到了一个更具学习理论的观点。在综合性论文 （Cheng等人，2016）中（其本身可以作为量子ML部分的综述） ，作者探讨了量子测量的可学习性问题。这可以被认为是本节前面讨论的学习量子态的双重任务。在这里，示例的形式为（ρ，Tr（ρE）），并且固定的是测量值。在这项工作中，作者计算了许多复杂性度量，这些度量与VC维密切相关（请参阅第II.B.1节），已知这些复杂性度量的样本复杂性范围。从这样的复杂性界限中，我们可以例如严格地回答各种相关的操作性问题，例如，我们平均需要准备多少个随机量子探针状态才能准确估计量子测量。作为标准估计问题的补充，这里我们不计算最优策略，而是有效地评估随机策略的信息增益。 这些度量是针对假设/概念系列计算的，这些假设/概念可以通过固定POVM元素（从而学习量子测量）或固定状态（即（Aaronson，2007）的设置）来获得，并清楚地说明 机器学习理论在QIP环境中的强大功能。

  b.量子学习RL的基础( Foundations of quantum-generalized RL ) 机器学习概念的大多数量子概括都完全在监督学习的领域中完成，只有少数例外。特别是在（Barry et al。，2014）中，作者介绍了 部分可观察的马尔可夫决策过程（POMDP）的量子一般化，在II.C节中进行了讨论。为了方便读者，我们简要回顾一下这些对象。完全可观察的MDP是任务环境的形式化：该环境可以处于代理可以观察到的任何数量的状态。 主体的行为a∈A触发环境状态的转变–转变是随机的，并由马尔可夫转变矩阵Pa.规定。另外，除了动力学之外，每个MDP都具有奖励函数R：S×A×S→Λ，该函数奖励某些状态-动作-状态转换。在POMDP中，主体看不到环境的实际状态，而只是观察到o∈O，这是环境状态的（随机）函数。尽管代理无法直接访问环境的确切环境状态，但鉴于系统的完整说明，给定交互历史，代理仍可以在状态空间上分配概率分布。 这称为 置信状态，可以表示为混合状态（混合“经典”实际环境状态），在POMDP状态基础上为对角线。量子化将环境置信状态提升为在希尔伯特空间上定义的任何量子状态，该希尔伯特空间由正交基{| si | s∈S}表示。量子POMDP的动力学是由与代理可以应用的量子工具（超级算子）相对应的动作定义的：对于每个动作a，我们将满足以下条件的Krauss算子集{Ka o}o∈O关联为P o Ka†oKa o =1。如果主体执行动作a，并观察到观察结果o，则环境状态将映射为ρ→KaoρKao†/ Tr [KaoρKao†]，其中Tr [KaoρKao†]是 观察到该结果的可能性。 最后，通过给定状态ρ的特定于动作的正算子Ra的期望值（Tr [Raρ]）来定义奖励。 在（Barry et al。，2014）中，作者从计算的角度研究了该模型，即从确定最佳的代理策略，将此设置与经典设置进行对比以及在证明分离的难度上进行了研究。特别是，对于有限的视野，决定政策存在的复杂性，对于量子案例和经典案例都是相同的。但是，可以找到关于目标可达到性问题的分离，该问题询问是否存在以概率1达到某个目标状态的（任何长度的）策略。 这种分离是最大的-这个问题在经典情况下是可以确定的，而在量子情况下是无法确定的。 尽管这种特定的分离可能不会对量子学习产生直接的影响，但它表明可能存在其他（戏剧性的）分离，并且具有更直接的相关性。