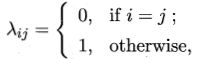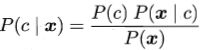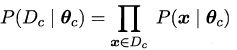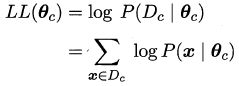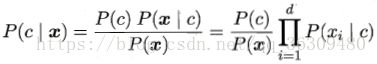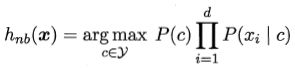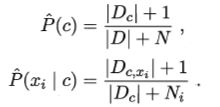机器学习笔记——贝叶斯分类器

一，贝叶斯最优分类器

期望损失（条件风险）：假设有N种可能的类别标记，即y = {c1,c2,...,cN}，λij是将一个真实标记为cj的样本误分类为ci所产生的损失。将样本x分类ci所产生的期望损失为：

我们的任务是寻找一个假设h，以最小化总体风险：

贝叶斯判定准则：为最小化总体风险，只需在每个样本上选择那个能使条件风险R(c|x)最小的类别标记，即：

此时，h*称为贝叶斯最优分类器，与之对应的总体风险R(h*)称为贝叶斯风险。

若目标是最小化分类错误率，则误判损失λij可写为：

此时条件风险：

贝叶斯最优分类器为：

即对每个样本x，选择能使后验概率P(c|x)最大的类别标记。

鉴于贝叶斯定理：

因此，估计P(c|x)的问题就转化为如何基于训练集D来估计先验P(c)和类条件概率（似然）P(x|c)。

二，极大似然估计

令Dc表示训练集D中第c类样本组成的集合，假设这些样本是独立同分布的，则参数θc对于Dc的似然是：

对θc进行极大似然估计，就是去寻找能最大化似然P(Dc|θc)的参数值θc。

通常对上式使用对数似然再求解参数：

这种估计方式结果的准确姓严重依赖于所假设的概率分布形式是否符合潜在的真实数据分布。

三，朴素贝叶斯分类器

估计后验概率P(c|x)的主要困难在于：类条件概率P(x|c)是所有属性上的联合分布，难以从有限的训练样本直接估计而得。

为避开这个障碍，朴素贝叶斯分类器采用了“属性条件独立性假设”：对已知类别，假设所有属性相互独立。

贝叶斯公式可重写为：

其中d为属性数目，xi为x在第i个属性上的取值。

朴素贝叶斯分类器的表达式为：

显然，朴素贝叶斯分类器的训练过程就是基于训练集D来估计类先验概率P(c)，并为每个属性估计条件概率P(xi|c)。

最后再来简单说一下拉普拉斯修正。具体来说，令N表示训练集D中可能的类别数，Ni表示第i个属性可能的取值数，则有：

显然，拉普拉斯修正避免了因训练样本不足而导致概率估值为零的问题。