证明可解汉诺塔问题:
我用的是数学归纳法,假设圆盘的个数为n,圆盘编号从上到下依次为1,2,3,4,……n,证明如下
①当 n = 1 时,从 A 移动到 C 显然能够完成,设需要移动的次数是a1。
②当 n = 2 时,由①可知从把 1 号盘子从 A 移动到 B能够完成(B 和 C 是等效的)此时移动次数为a1。
之后把2号盘子移动到C上面此时移动次数为a1 + 1。
这时把1号盘子从B移动到C和①是等价的,
移动后总的移动次数是a2 = a1 + 1 + a1。
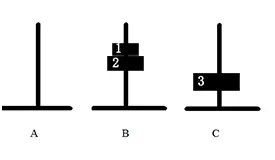
③当n = 3时,由②可知移动成下图的效果是可以实现的,
此时移动的次数是a2,接着把3号盘子移动到C上面
此时移动的次数是a2 + 1,这时把1和2号盘子移动到C上面(移动过程中3号盘子始终不会动)和②等效的,移动完成之后如下
移动的总次数是a3 = a2 + 1 + a2
④当n=4时,由③可知移动成下图的效果是可以实现的,
此时移动的次数是a3
把4号盘子从A移动到C
此时移动的次数是a3 + 1
接下来把123号盘子从B移动到C的过程又和③等效了移动之后如下
移动的总次数是a4 = a3 + 1 + a3
假设当n= k时,从A移动到C是可以实现的,那么当n=k+1时,可以移动到A上面只剩k+1号盘子,B上面依次是1,2,3,.....,k号盘字,此时移动次数是ak
把k+1号盘子移动到C上面,这时移动次数是ak + 1
接下来和n=k时移动过程等效,移动完成后移动总次数是ak+1 = ak + 1+ ak
可以得知移动k+1个盘子需要的次数与移动k个盘子的次数之间的关系是:
ak+1 = ak + 1+ ak = 2ak + 1
所以ak+1 + 1 = 2*(ak + 1)【这是个等比数列高中学过的】
即ak + 1 = (a1 +1)* 2n-1 = 2n 因此ak = 2n - 1
至此,证明完毕。