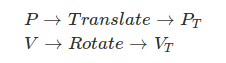零基础学图形学(2) 几何知识——点,向量,法向量
1. 点,向量,法向量
2. 坐标系统
3. 点和向量的数学操作
4. 矩阵
5. 矩阵介绍
6. 点和向量变换
7. 行向量和列向量
8. 矩阵操作
9. 球坐标系和三角函数
10. 创建矩阵和本地坐标系统
11. 法向量变换
12. 源码
关键字: 向量,点,矩阵,法向量,变换,笛卡尔坐标系, 笛卡尔坐标,球坐标,坐标系
几何学是数学的一个分支,主要涉及的是形状,大小,相对位置,空间等属性。
警告:这个教程对于大多数的读者来说非常的长而且有难度,如果你是一个计算机图形学新人,那么你应该花时间详细地重头开始阅读。完全掌握这部分的计算机图形学的知识非常重要,它是你学习后面的基础,而且会节省你非常多的时间。
(1)几何学介绍
点,向量,矩阵,法向量,对于计算机图形学的重要性就像字母表对于文学的重要性一样;因此很多关于计算机图像学(Computer Graphic 后面都简称CG)的书从讲述现行袋鼠和几何开始。但是,对于很多想学习图形学编程的人来,一开始展现了太多的数学知识会让他们感觉到不安。如果你因为感觉不能掌握数学知识而对CG编程不适合你,不要现在就放弃。
我们从3D渲染基础开始,这里不需要任何线性代数的预备知识。这是一个不寻常的教授CG编程的方式,我们相信你会对一些实用的有兴趣的会更感兴趣。比如,介绍光线追踪只需要很少的数学知识和一些编程知识。编写一个渲染起更有趣也是学习数学的一个很好的办法,这个过程中你可以知道怎么实用学到的知识生成具体的结果(一副图片)。那也就是说,点,向量,和矩阵在生成CG图像上很有作用的,在余下的每篇教程中都会用到它们。
这篇教程中,你会学习到它们是怎么构成的,它们是怎么工作的,以及各种如何使用和操作它们的技术。这篇教程也解释了CG研究人员在解决它们写程序时遇到的问题的各种方法。你需要意识到这些方法不会在书中或者网络中提及。这些方法很重要,在你阅读和使用其它的开发这的代码或者技术的时候,你必须首先知道它们使用的方法。
在我们开始阅读之前,有点需要告诉大家的是,如果你是一个数学学究,你可能发现这里的数学知识解释很简单,并不是严格的和线性代数相关。我们保证这篇教程可以更广泛,以及包括简单的使用在CG中的向量和矩阵的数学知识。比如,一个点,从数学角度来说,在线性代数上并不会讲述。如果你现在不知道点和向量之间的区别,不用着急,我们会单独有涨讲到它们。
(2)什么是线性代数?向量介绍
线性代数准确来说是什么呢?这章我们会学习到什么呢?结项我们在之前的章节中提到的,线性代数是数学的一个分支,它是用来研究向量的。现在你可能问,什么是向量,它在CG世界中有什么用?我们不会太深入细节,但是一个向量可以用一个存放数字的数组表示。这个数组是数字的组合,它可以表示任意的长度,在数学上有时它称作元组。如果我们想要表示具体的向量的长度,可以使用n维元组表示,这里的n表示向量元素的个数。下面是一个数学公式的例子,这个向量有6个元素:
$$V = (a, b, c, d, e, f)这里a, b, c, d, e, f都是实数。
把这些数字组合起来可以更好地表示另一个在其它问题上有意义的概念。比如,在计算机图形学中,向量可以表示一个位置或者空间的方向。我们也会通过通过一系列的操作变换这些向量。处理向量变换的过程我们称之为线性变换。我们会在下面的教程中花大量的时间讲述变换,现在,只需要知道它们很重要就可以了。
(3)点和向量
在不同的领域不同的场合中都会用到点和向量。这个小节中,我们会讲述关于这个教程和计算机图形相关的点和向量知识。
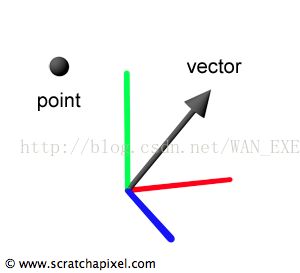
下图展示坐标系中的点和向量。
这里,一个点是三维坐标空间的一个位置。一个向量,从另一个角度来说,通常表示一个三维坐标空间的方向。一个向量可以想象成可以指向各个方向的箭头。三维的点和向量当然和之前提到的元组是一样的。
$$V = (x, y, z)记住,当和数学家或者物理学家提到它们的时候,它们理解的向量或者点会更加通用。它们不会被限制在只使用在CG上。对它们来说,一个向量可以是任意的大小(可以含有任意多个数)。
我们简短地介绍齐次点(homogeneous points)结束这章。有时候为了数学上计算方便必须增加第四个元素。下面是一个齐次坐标点:
$$P_H = (x, y, z, w)在用到点和矩阵相乘时齐次坐标点会很有用。现在不用太担心它们具体的含义。我们只是提到因为在后面出现的时候不会让读者感到迷惑,后面还会具体地介绍它们的。
(4)变换(transformation)的快速介绍
你可能还在想一个线性变换会在点或者向量中有什么作用。其实它很简单,一个通常的操作就是我们会在空间中通过线性变换移动它们。这个变换有个更具体的称呼叫做移动(translation),它在渲染中有很重要的作用。
移动操作无非就是对原有点进行线性变换。对于向量(记住它是方向)来说,移动是没有意义的。这是因为向量的开始点并不重要;不管起始点,所有的相同长度的箭头,指向相同方向的向量都是等价的。但是,我们经常使用另外一个线性变化在向量上,那就是旋转(rotation).更多常见的操作可以被使用,但是现在只需要考虑点的移动和向量的旋转。
T下表表示变换。
像你现在所看到的,我们并没有讨论向量的长度或者是标量。确实,在CG中向量的长度有很重要的功能。当向量的长度为1时,我们成这个向量为单位向量(Normalised 我们会一直看到这个词汇)。将向量变成坐标向量需要改变向量的长度为1,方向不发生变化。很多时候,我们都需要单位向量,但是也有些时候我们需要向量的长度表示一些有意义的东西。
比如,想想你从一点A移动到另外一点B,这条移动的线创建了一个向量,它表示这样一个场景:B相对于A的位置。那也就是说,就像你站在A处观察B一样。这里向量的长度意味着A到B的距离,求距离可能需要一些算法。
向量的单位化经常会在程序中出问题,因此在每次你申明向量的时候,我们建议你持续地问你自己这个向量是否应该被单位化。
(5)法向量(Normals)
法向量是用来描述一个几何物体表面点的方向的,从技术上来说,P点表面的法向量,可以看做是垂直于P表面的的向量。在渲染中法向量扮演很重要的角色,它们用来计算物体的明暗程度(在后面的文章中会介绍)。
下图是法向量表示:
法向量可以看着是一个有附加说明的向量:它们不能像向量那样变换。这是我们区分它们的主要因素,你可以在法向量变化章节发现更多法向量相关的知识。对于现在,你只需要知道它们是什么就可以了。
(6)从理论到编码
在我们的C++代码中,我们不会区分点,向量和法向量。它们都用一个Vec3的类表示(我们使用模板类,因此可以根据需要创建整型,小数点型等数据。一些开发者喜欢区别它们,这可以减少发生错误的可能。从经验上来说,我们发现使用一个统一的类会更有效可以写更少的代码(就像OpenEXR库那样)。但是,我们仍然不得不在几个具体的函数上对于是否调用点,向量,或者法向量作区别。正如你应该记得,这个对于变换十分重要,完整的代码在这个章节的最后面提供下载。
template
class Vec3 {
public:
// 3 most basic ways of initializing a vector
Vec3() : x(T(0)), y(T(0)), z(T(0)) {}
Vec3(const T &xx) : x(xx), y(xx), z(xx) {}
Vec3(T xx, T yy, T zz) : x(xx), y(yy), z(zz) {}
T x, y, z;
};
typedef Vec3 Vec3f; Vec3 a;
Vec3f b; 从这章中,你应该记住数学上向量可以任意维度。但是在CG中,我们使用更具体的向量:一个在3D空间的向量(因此只用三个数字表示)。另外,三维坐标系中的点也是用三个数字表示。齐次坐标点是一个特殊的示例,它有四个数字。
点和向量可以使用线性变换进行变换。
你可以经常看到线性变换,如果在变换的过程中线段保持不变,我们称之为线性变换(相当于乘以一个矩阵的线性变换)。
典型的这种变换比如点的移动,和向量的旋转。如果向量的长度为1,则称它为单位向量。在被单位化之前,向量的长度表示两个点之间的距离,有时需要特定的算法计算它们。所以,开发者对是否以及何时选择单位向量要小心。
(8)下一节
我们还没有解释的一个重要的事情是三个数字定义的点和向量表示什么。这些数字表示二维或者三维空间的点坐标,相对于原点坐标来说的。这个相对值,我们称之为坐标系统,是下一节的主题。