量子领域的机器学习&人工智能（一）

原文作者：Vedran Dunjko；Hans J. Briegel
翻译者：Wendy

摘要（ Abstract）

  量子信息技术和只能学习系统都是新型的技术，它们很可能在未来对我们的社会产生变革性的影响。各个基础研究领域–量子信息（QI）与机器学习(ML)和人工智能（AI）–各自都有特定的问题和挑战，迄今为止，这些问题和挑战已被大量独立研究。然而，在最近的工作中，研究人员一直在探索这些领域在多大程度上可以真正相互学习和受益的问题。QML探索了量子计算与机器学习之间的相互作用，研究了如何将一个领域的结果和技术用于解决另一领域的问题。最近，我们见证了两个方面的重大突破。 例如，量子计算在加快机器学习问题的速度中找到了至关重要的应用，这对于“大数据”领域至关重要。相反，机器学习已经渗透到许多尖端技术中，并可能成为先进量子技术的重要工具。 除了数据分析中的量子加速或量子实验中使用的经典机器学习优化之外，理论上还证明了交互式学习任务的量子增强，突出了量子增强的学习代理的潜力。最后，探索将人工智能用于量子实验的设计以及自主进行部分真正研究的工作，报告了他们的首次成功。 除了相互增强的主题（探索ML / AI对量子物理学的作用，反之亦然）之外，研究人员还提出了学习和AI概念的量子概括的基本问题。 这涉及在量子力学充分描述的世界中学习和智力的意义的问题。 在这篇综述中，我们描述了在量子领域研究机器学习和人工智能的广泛研究中的主要思想和最新进展。

Ⅰ 引言（ INTRODUCTION）

  量子理论影响了物理学的大多数分支。 这种影响的范围从较小的校正到彻底的大修，尤其是在处理规模足够小的领域中。在上个世纪下半叶，很明显的是，真正的量子效应也可以用在工程类型的任务中，而且这种效应所具有的功能要优于纯经典系统所能实现的。在这种工程中的应用，第一波浪潮给了我们例如激光器，晶体管和核磁共振设备。 第二波浪潮是在1980年代发展起来的，它构成了一个大规模的（尽管不是完整的系统）研究，涉及使用量子效应完成各种类型任务的潜力。它在此基础上处理信息。这包括密码学，计算，传感和计量学的研究领域，所有这些领域现在都共享量子信息科学的通用语言。 通常，对此类跨学科计划的研究非常有成果。例如，量子计算（QC），通信，密码学和计量学现在已经成熟，完善且具有影响力的研究领域，可以说已经彻底改变了我们对信息及其处理的思考方式。近年来，显而易见的是，量子信息处理与人工智能和机器学习领域之间的思想交流有其自身的真正问题和希望。尽管此类研究才刚刚得到广泛的认可，但最早的想法已经在量子计算的初期出现，我们已经竭尽全力公平地认可了这些有远见的作品。

  在这篇综述中，我们的目的是在广泛的范围内，以具有物理背景的读者为对象，对机器学习，人工智能和量子力学之间的相互作用研究进行阐述。因此，我们在经典的机器学习和人工智能方面有相对较大的篇幅，这些主题通常在面向物理学的文献中有所提及，同时保持量子信息方面的简洁性。

  本文的结构如下。在本引言的第一部分的其余部分中，我们快速概述了场量子信息处理，机器学习和人工智能的相关基本概念。我们在引言中提供了有用的术语表，简写列表以及对注释的注解。随后，在第二部分中，我们将深入研究经典理论的选择方法，技术细节和理论背景。从经典写综述的角度来看，这里主题的选择不一定是平衡的。我们将重点放在出现在随后的量子提案中的元素上，这些元素有时可能有些奇怪，或者着重于有助于将量子结果的相关性置于适当背景下的方面。第三节简述了本综述的量子部分所涵盖的主题。 第四节至第七节涵盖了我们调查的四个主要主题，并且构成了本文的核心内容。 我们在展望部分中完成了第八部分。

  备注： 这篇综述的总体目标是对主题进行宽泛的“鸟瞰”，这些主题有助于发展量子信息科学与机器学习和人工智能之间相互作用的各个方面。因此，本综述并不一定以完全平衡的方式呈现所有发展。与较发达的主题相比，某些主题处于研究的早期阶段，但对新生的研究领域很重要，它们的关注程度可能不成比例。例如，这在第七节中尤为明显，该节旨在解决量子人工智能的主题，超越了机器学习的主流数据分析应用。该主题与对新兴领域的广阔视野有关，但是只有极少数的作者，著作（包括本综述的作者和合作者）才提出这个话题。最近在较集中的评论中解决了更广泛探索的主题，例如用于机器学习和数据挖掘的量子算法，量子计算学习理论或量子神经网络。 (Wittek, 2014a; Schuld et al., 2014a; Biamonte et al., 2016; Arunachalam and de Wolf, 2017; Ciliberto et al., 2017).

A. 量子力学、量子计算、量子信息处理技术（ Quantum mechanics, computation and information processing）

执行摘要：量子理论导致许多违反直觉和令人着迷的现象，包括量子信息处理领域，尤其是量子计算领域的结果。 该领域研究了量子信息的复杂性，其通信能力，处理技术。量子理论解释了许多经典物理学中不可解释的现象。例如，量子信息无法克隆–这限制了一般量子信息可能进行的处理类型。其他方面也带来了优势，正如针对各种通信和计算任务所显示的那样：解决代数问题，降低黑盒设置中的样本复杂度，抽样问题和优化。甚至适用于近期实现的受限量子计算模型也可以解决有趣的任务。机器学习和人工智能任务可以作为组件依赖于解决此类问题，从而获得优势。

  通常在量子信息中介绍的量子力学都是要基于一些简单的假设：1）量子系统的纯态由复希尔伯特空间中的单位矢量|ψ>给出；2）密闭系统纯状态演化是由哈密顿量H生成的,由线性薛定谔方程指定 H|ψ>iℏ (∂/∂t)|ψ>；3）复合系统的结构由张量积给出；4）理想情况下，投影测量（可观测值）由非退化的哈密顿算子指定，并且测量过程将观测系统的描述从状态|ψ>变为本征状态|φ>的概率由伯恩规则p（φ ）= |<ψ|φ>| ²给出。虽然完整的理论仍然需要处理子系统和经典的不确定性，但已经有一些纯状态封闭系统理论的数学公理引起许多典型的量子现象，例如叠加，无克隆，纠缠等，其中大部分只是源自线性理论。这些特性中的许多特性重新定义了量子信息研究人员如何看待信息，同时在量子增强密码学，通信，传感和其他应用中也起着至关重要的作用。量子理论最令人着迷的结果之一，可以说是量子信息处理（QIP）领域，尤其是量子计算（QC）领域所捕捉到的，这与我们本综述的目的最相关。

  QC彻底改变了计算的理论和实现方式。该领域源自Manin和Feynman的观察，即随着时间的推移，量子系统某些性质的计算可能是棘手的，而量子系统本身以某种方式 讲，仅仅通过发展就可以完成那困难的计算。自从这些早期思想问世以来，量子计算就已经激增，实际上，可伸缩通用量子计算机所具有的量子优势已经在许多场合得到了证明。也许最著名的是，量子计算机已被证明可以有效解决经典计算难以解决的代数计算问题。这包括著名的因数分解大对数以计算离散对数的问题，还包括许多其他问题，例如Pell方程求解，一些非阿贝尔隐式子组问题以及其他一些问题，例如参见 （Childs and van Dam，2010; Montanaro，2016）进行的论述。 与此相关的是，如今我们也可以访问越来越多的量子算法集合用于各种线性代数任务，例如 （Harrow等，2009； Childs等，2015； Rebentrost等，2016a），这可能会加快速度。

  量子计算机还可以改善许多优化和仿真任务，例如，计算分区函数的某些属性，模拟退火，求解半定义程序，求解近似优化以及自然模拟量子系统的任务。

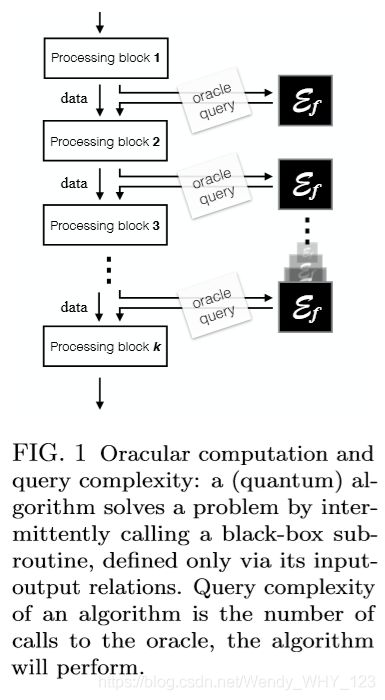
  在有效使用子例程和数据库方面也有很大的优势。这是使用oracular 计算模型进行研究的，其中感兴趣的数量是对oracle（具有定义好的输入输出关系集的黑匣子对象）的调用次数，抽象地代表数据库，子例程或 任何其他信息处理资源。在这种情况下，量子优势的典型例子是格罗弗（Grover）的 搜索算法（Grover，1996），该算法在无序搜索（以oracle为数据库）中实现了可证明的最佳二次改进。在许多其他情况下也获得了类似的结果，例如空间搜索（Childs和Goldstone，2004年），结构搜索（包括各种基于量子步行的算法（Kempe，2003年； Childs等人，2003年； Reitzner等人） （2012年），NAND（Childs等人，2009年）和更常见的布尔树评估问题（Zhan等人，2012年）以及最新的“备忘单”技术结果（Aaronson等人，2016年） 导致比二次更好的改进。从更广泛的意义上讲，还可以使用oracular计算模型来对 通信任务 进行建模，其目的是降低某些信息交换协议的通信复杂性（即通信回合数）（de Wolf，2002）。量子计算机也可以用于解决 采样问题 。 在抽样问题中，任务是根据（隐式）定义的分布来产生样本，这对于优化和代数任务（某些实例）都非常重要。

  例如，马尔可夫链蒙特卡罗方法，可以说是自然科学中最丰富的计算方法集，旨在解决采样任务，而采样任务又可以用来解决其他类型的问题。例如，在统计物理学中，从Gibbs 分布采样的能力通常是计算 分区函数属性 的关键工具。解决抽样问题的一类广泛的量子方法集中于此类马尔可夫链方法的量子增强（Temme等人，2011； Yung和Aspuru-Guzik，2012）。QIP社区中的采样任务受到越来越多的关注，我们将在后面进行详细论述。量子计算机通常以几种标准的计算模型之一形式化，从计算上讲，其中许多功能同样强大。即使模型在计算上是等效的，但它们在概念上是不同的。因此，对于给定的应用程序类别，某些组件更合适或更自然。 历史上，出于理论和可计算性的考虑，首选第一个正式模型是量子图灵机（Deutsch，1985）。量子电路模型（Nielsen和Chuang，2011）是代数问题的经典模型。基于测量的量子计算 （MBQC）模型 （Raussendorf和Briegel，2001; Briegel等，2009）可以说 最适合图相关的问题 （Zhao等，2016），多方任务、分布式计算（Kashefi和Pappa，2016）和盲量子计算（Broadbent等，2009）。 拓扑量子计算 （Freedman等，2002）是某些打结理论算法（Aharonov等，2006）的灵感来源，与拓扑纠错和容错算法密切相关。绝热量子计算模型（Farhi et al。，2000）的构建考虑了基态准备的任务，因此 非常适合优化问题 （Heim et al。，2017）。

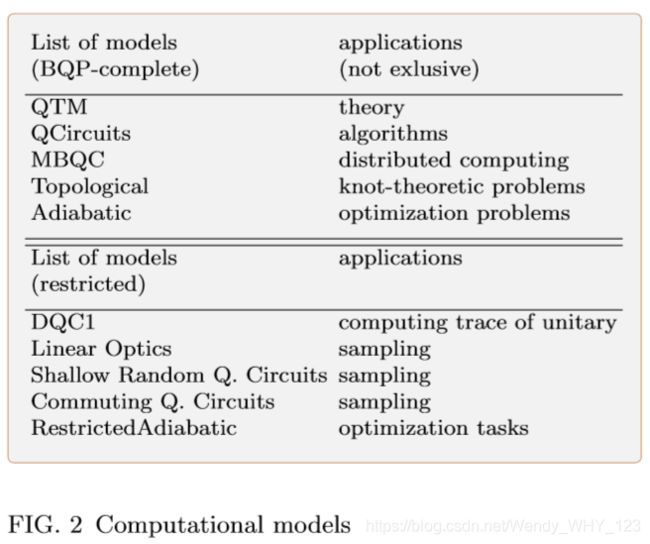
  对QIP的研究还产生了一些有趣的受限计算模型示例：有效的QC不可能是通用的模型，但是仍然可以解决传统机器似乎很难完成的任务。最近，人们对这种模型越来越感兴趣，特别是线性光学模型，所谓的低深度随机电路模型和换向量子电路模型。在（Aaronson和Arkhipov，2011）中，证明了线性光学模型可以有效地从某些矩阵的永久性所指定的分布中生成样本，并且证明了（除非某些合理的数学猜想），经典计算机无法从这些样本中复制多项式时间相同的分布样本。 对于低深度随机电路（Boixo等，2016; Bravyi等，2017）和仅包括换向门的换向量子电路（Shepherd和Bremner，2009; Bremner等，2017）也提出了类似的主张。 至关重要的是，可以 将这些受限制的模型实现为足够大的规模，以便演示使用近期技术无法进行的计算，这些计算是当前可用的最强大的经典计算机无法实现的。这个里程碑被称为 量子至上（Preskill，2012; Lund et al。，2017），近来引起了极大关注。QIP的另一个活跃领域集中于（模拟）量子模拟，并应用于量子光学，凝聚态系统和量子多体物理学中（Georgescu等，2014）。上述量子计算的许多方面（如果不是大多数的话）正在量子机器学习应用程序中起作用。

  接下来，我们简要回顾一下人工智能和机器学习的经典理论中的基本概念。

B. 人工智能和机器学习（ Artificial intelligence and machine learning）

执行摘要：人工智能领域结合了各种方法，这些方法主要集中于解决计算机难以解决但对人类而言似乎容易解决的问题。这类任务中最重要的一类也许是学习问题。机器学习领域解决了学习问题的各种算法问题，而机器学习领域是从AI上下文中的模式识别研究发展而来的。现代机器学习解决了各种场景的学习，例如从数据中学习数据。 有监督的（数据分类）和无监督的（数据聚类）学习，或来自交互的学习，例如 强化学习。现代AI的终极目标是，设计一种在未知环境中学习和发展的智能代理模型。从一般意义上讲，具有人类智能的人工代理必须具有解决机器学习和AI的其他更专业分支所解决的所有单个问题的综合能力。 因此，它们将需要复杂的技术组合。

  在最广泛的范围内，现代人工智能领域涵盖了各种各样的子领域。这些领域中的大多数都涉及对各种人类能力的理解和抽象，我们将它们描述为智能的，并试图在机器中实现相同的能力。“ AI”一词是在1956年的达特茅斯学院会议上提出的（Russell和Norvig，2009年），这些会议的目的是发展有关可以思考的机器的思想，而这些会议通常被称为该领域的发源地。这些会议的目的是“找到如何让机器使用语言，形成抽象和概念，解决现在人类所面临的各种问题以及改善自身的能力” 。该领域的历史一直动荡不安，对如何实现AI有着强烈的看法。 例如，在最初的30年中，该领域已经就如何实现AI形成了两种主要的相互对立的观点（Eliasmith和Bechtel，2006年）：计算主义–认为大脑通过执行纯粹的形式运算而起作用 在符号上，以图灵机的方式，例如 （Newell and Simon，1976））和 连接主义–将心理和行为现象建模为模仿生物大脑的简单单元相互连接的网络的新兴过程，例如 （Medler，1998）。这两种观点仍然影响着AI的发展。 不管潜在的哲学如何，在AI历史的大部分时间里，“真正的AI”的实现据说永远是“数年之久”的，这一特性通常也被领域的批评者归因于 量子计算机。在人工智能的情况下，这种失控的乐观情绪在很多情况下对领域造成了严重的灾难性影响，尤其是在资金方面（导致现在被称为“人工智能的冬天”）。 到90年代后期，该领域的声誉很低，即使事后看来，对于为什么AI无法产生人类水平智能的原因也没有达成共识。 这些因素在将AI划分为多个子领域中起着至关重要的作用，这些子领域专注于专门任务，通常以不同的名称出现。

  Brooks倡导了一种特别有影响力的AI视角，通常被称为“新手”或“体现的AI”，该观点认为，情报来自（简单的）体现系统中，这些系统通过与环境交互来学习（Brooks，1990）。与当时的标准方法相反，Nouvelle AI坚持学习而不是预先编程属性，而是坚持AI实体的体现，而不是像国际象棋程序这样的抽象实体。对于物理学家来说，这种体现智能的观点使人联想到信息是物理的观点，这种观点一直是“量子信息理论的集会号召”（Steane，1998）。此类体现的方法在机器人技术中尤为重要，其中关键问题涉及感知（机器使用其传感器解释外部世界的能力，包括计算机视觉，机器听觉和触摸），运动和导航（例如在自动驾驶汽车中很重要） 。 与人机界面相关，人工智能还整合了自然语言处理领域，其中包括语言理解–机器从自然语言中获取含义的能力，以及语言生成–机器以自然语言传达信息的能力。

  人工智能的其他一般方面涉及对智能实体的一些经过充分研究的能力（Russell和Norvig，2009）。 例如，自动计划与决策理论有关，广义上讲，它是确定战略（即一系列行动）以实现目标而必须执行的任务，同时将（指定的）成本降至最低。 所谓的在线计划任务已经很简单了，其中的任务，成本函数和可能采取的行动是事先已知的，其中包含了真正的难题。 作为特殊情况，它包括NP-完全难题，旅行商问题（TSP）； 有关说明，请参见图3。

  在现代，TSP本身不再被视为真正的AI问题，而是用来说明AI已经非常专业，简单的子任务可能会很难。更一般的规划问题还包括在线变体，在这种变体中，并非事前都知道所有事情（例如，TSP，但“地图”可能无法包括所有可用的道路，而实际上必须行事以找到好的战略）。 在线计划与强化学习重叠，本节稍后将进行讨论。 与计划紧密相关的是智能实体解决问题的能力。 在技术文献中，解决问题与计划的区别在于计划中通常假定的问题缺乏附加结构，换句话说，解决问题比计划更笼统，定义更广泛。一般问题解决中缺乏结构，这与（和非结构化的）搜索和优化建立了明确的联系：在没有其他信息或结构的情况下，问题解决是寻找精确指定问题的解决方案。从理论上讲，一般的问题解决可以通过一般的搜索算法（仍然可以细分为诸如深度优先，呼吸优先，深度受限的搜索等类别）来实现，但问题的结构却更多， 在这种情况下，明智的搜索策略（通常称为启发式搜索策略）将更加有效（Russell和Norvig，2009）。人类智能在很大程度上取决于我们的知识。 我们可以积累知识，对其进行推理，然后将其用于做出最佳决策， 例如在解决问题和计划的背景下。 AI的一个方面试图形式化这种逻辑推理，知识积累和知识表示，通常依赖形式逻辑，最常见的是一阶逻辑。

  与AI息息相关的特别重要的一类问题是机器通过经验学习的能力。 在AI的早期阶段就已经强调了这一功能，现在可以推论得出的机器学习（ML）领域是AI最为成功的方面（或自旋），我们将对此进行更详细的介绍。

1. 从数据中学习：机器学习（ Learning from data: machine learning）

  机器学习从传统的模式识别出发，例如手写文本识别和统计学习理论（将机器学习的思想置于严格的数学框架中），从广义上讲，机器学习探索了可以从数据中学习规律并做出数据预测的算法 。 传统上，机器学习的两种主要的学习问题：有监督学习和无监督学习，这与数据分析和数据挖掘类型的任务密切相关（Shalev-Shwartz和Ben-David，2014年）。 关于该领域的更广泛的观点（Alpaydin，2010）还包括强化学习（Sutton和Barto，1998），这与生物智能实体所实现的学习密切相关。 我们将单独讨论强化学习。

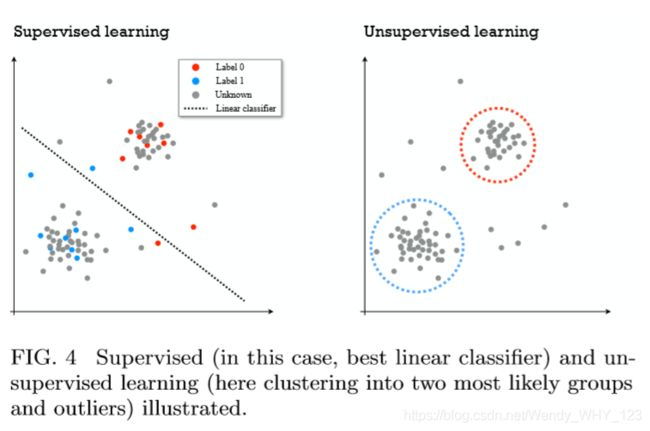
  从广义上讲，监督学习以示例学习的方式进行处理：给定一定数量的标记点（所谓的训练集）{（x_i，y_i）}_ i，其中x_i表示数据属性，例如N维向量和y_i表示标签（例如二进制变量或实数值），任务是推断“标签规则” x_i →y_i，它使我们能够猜测先前未见数据的标签，即训练集。 从形式上讲，我们处理基于以下条件得出的一定数量的样本来推断条件概率分布P（Y = y | X = x）（更具体地说，生成一个标记函数，该函数可能以联合概率分布P（X，Y）方式将标记分配给点）。例如，我们可以推断出特定的DNA序列是否属于可能患糖尿病的个体。这样的推论可以基于已经记录了DNA序列的患者的数据集，以及有关他们是否真正患上了糖尿病的信息。在此示例中，变量Y（糖尿病状态）为二分类，并且标签的分配不确定，因为糖尿病也取决于环境因素。另一个示例可能包含两个实数变量，其中x是物体降落的高度，y是跌落的持续时间。在此示例中，两个变量都是实值，并且（在真空中）标记关系基本上是确定性的。在无监督学习中，仅为数据点提供不带标签的算法。广义上讲，此处的目标是识别数据集中的基础分布或结构以及其他信息特征。换句话说，任务是根据一定数量的样本（相对于用户指定的准则或规则）推断分布P（X = x）的属性。无监督学习的标准示例是聚类任务，其中应该将数据点分组的方式最小化组内平均距离，同时最大化组间的距离。 请注意，可以将组成员身份视为标签，因此这也对应于标签任务，但是缺少“监督”：正确标签的示例。在此类任务的基本示例中，预期群集的数量由用户给出，但这也可以自动优化。

  其他类型的无监督问题包括 特征提取和降维，这对于应对所谓的维数诅咒至关重要。维度诅咒 指的是：现实生活数据的原始表示经常占据非常高的维度空间。例如，在标准刷新频率下的一秒钟分辨率为标准分辨率的视频片段，即使事件携带相关信息（例如，许可证的牌照号），其捕获的事件也会在时间上映射到约10^8维空间中的矢量。拍摄的超速驾驶汽车）可能会小得多。更一般地，直观上很明显，由于几何体积随其所在空间的大小呈指数比例缩放，因此捕获（或学习）n维对象的一般特征所需的点数也将呈指数比例缩放。换句话说，在高维空间中学习是指数困难的。因此，在任何现实生活中，从原始表示空间（例如，移动的汽车夹子）到相关特征空间（例如，牌照号）的降维方法都是必不可少的。

  这些方法试图将数据点缩小到一个显着减小的空间，同时尝试维护数据结构的主要特征（相关信息）。降维技术的典型示例是主成分分析技术（PCA）。 在实践中，此类算法还构成了数据预处理中其他类型学习和分析的重要步骤。 此外，此设置还包括生成模型（与密度估计有关），其中基于少量精确样本生成来自未知分布的新样本。 随着人类以指数级的速度收集数据（insideBIGDATA，2017），以自动化的方式提取真正有用的信息变得越来越重要。 在现代世界中，无处不在的大数据分析和数据挖掘是有监督和无监督学习的核心应用。

2. 交互中学习：强化学习（ Learning from interaction: reinforcement learning）

  传统上，强化学习（RL）（Russell和Norvig，2009； Sutton和Barto，1998）是ML的第三种规范类别。 部分由于在数据挖掘和大数据分析主题的背景下（无）监督的方法的普及，许多关于ML的现代教科书都将重点放在这些方法上。 RL策略大部分仍然保留给机器人技术和AI社区。 但是，最近，对自适应和自主设备，机器人技术和AI的兴趣激增，使得RL方法的重要性日益增强。

  最近一项依赖于标准ML和RL技术的广泛使用，这就是著名的AlphaGo结果（Silver等，2016），它是一种学习系统，掌握了围棋游戏，可以说很容易地实现了超人的表现。 击败了最厉害的人类玩家。 这个结果之所以引人注目，原因有很多，其中包括一个事实，它说明了在人工智能问题中学习机相对于专用求解器的潜力：而依赖于学习编程的专用设备（如Deep Blue）可能会超越人类的表现 在国际象棋中，他们没有为更复杂的围棋做同样的事情，围棋的策略空间更大。 学习系统AlphaGo比典型的预测早了很多年。从量子信息的角度来看，RL和其他数据学习ML方法之间的区别特别重要，这将在VII.B节中详细介绍。 RL构成了广泛的学习环境，是在AI的一般代理人环境范式（AE范式）中提出的（Russell和Norvig，2009）。 在这里，我们不处理静态数据库，而是处理交互式任务环境。 学习代理（或学习算法）通过与任务环境的交互来学习。

  作为说明，可以想象一个机器人，它在环境中作用，并通过其传感器感知–感知是例如其视觉系统拍摄的快照，而动作是例如机器人的运动–如图所示 5。但是，AE形式主义更为笼统和抽象。它也是不受限制的，因为它还可以表示受监管的设置和不受监管的设置。 在RL中，通常假设过程的目标体现在奖励函数中，大致来说，只要代理行为正确（在这种情况下，我们要处理积极的强化，但其他方式都是也使用操作条件） 。这种学习模型似乎很好地涵盖了大多数生物因子（即动物）的学习方式：可以通过训练狗以欺骗技巧的过程来说明这一点，方法是在狗表现良好时给予奖励。如前所述，RL完全是在给定的接收条件下，在完全在线的环境中学习如何执行“正确”的动作序列，这是计划的一个方面：了解环境的唯一方法是通过与之互动。

3. 中间学习设置（ Intermediary learning settings）

  监督学习，无监督学习和强化学习构成了三大类学习，但存在许多变化和中介环境。例如，半监督学习就是介于无监督和监督学习之间的一种学习设置，其中与总可用训练集相比，有标签的数据非常少。但是，即使是少数标记示例也已显示出可以改善无监督学习的性能（Chapelle等人，2010），或者，从相反的角度来看，当面对少量标记示例时，未标记数据可以帮助分类。在有监督学习中，学习算法可以进一步向人类用户或主管查询特定点的标签，以提高算法的性能。仅当用户在操作上可能正确地标记所有点时才可以实现此设置，并且当此精确的标记过程很昂贵时可能会产生好处。 此外，在有监督的设置中，可以考虑所谓的归纳学习算法，该算法基于训练数据输出分类函数，该分类函数可用于标记所有可能的点。分类器只是一个将标签分配给数据域中的点的函数。 相反，在半监督学习中（Chapelle等，2010），需要稍后标记的点是事先已知的-换句话说，分类函数仅需要在先验已知点上定义。接着，有监督的算法可以执行惰性学习，这意味着将整个标记的数据集保留在内存中以标记未知点（然后可以添加），或者急切学习，在这种情况下，将输出（总计）分类器功能 （并且不再明确要求训练集）（Alpaydin，2010年）。渴望学习的典型例子是线性分类器，例如下一节中描述的基本支持向量机，而懒惰学习的例子是例如“ 最近邻方法”。我们的最后一个例子，在线学习（Alpaydin，2010年）可以理解为急切的有监督学习的扩展或RL的特殊情况。 在线学习概括了标准的有监督的学习，在这种意义上，训练数据被顺序地提供给学习者，并用于增量地更新分类功能。 在某些变体中，要求算法对每个点进行分类，然后再给予正确的响应，并且性能基于猜测。 猜测与实际标签的匹配/不匹配也可以理解为一种奖励，在这种情况下，在线学习成为RL的受限情况。

4. 放在一起：代理人-环境范例（ Putting it all together: the agent-environment paradigm）

  前面提到的专业学习场景可以用统一的语言表述，这也使我们能够讨论如何以实现真正的AI为目标来满足专业化的任务。

  在现代的人工智能研究中（Russell和Norvig，2009），该理论的核心概念是代理的概念。 代理是相对于其环境定义的实体，并且具有行动的能力，即可以做某事。

  用计算机科学术语来说，将某物作为代理（或要采取行动）的要求是最低的，并且基本上所有东西都可以被视为代理，例如，所有非平凡的计算机程序也是代理。

  人工智能更多的与代理商有关，例如，他们也感知自己的环境，与之交互并从经验中学习。 如今，AI被定义为旨在设计智能代理的领域（Russell和Norvig，2009），这些代理具有自主性，可以使用传感器感知自己的世界，使用执行器对其进行操作，并选择其活动以实现某些目标：在文学中也称为理性的属性。

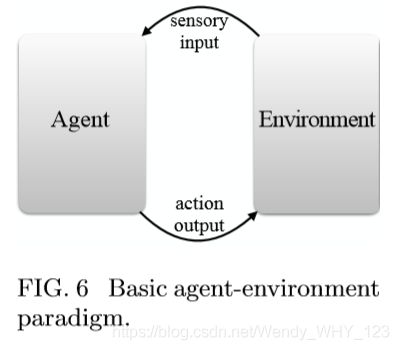
  代理仅相对于与它们交互的环境（更具体地讲是任务环境）存在，构成了整个AE范例，如图6所示。虽然在考虑代理时可以方便地描绘机器人，但它们也可以更加抽象虚拟的，就像互联网上“活着”的计算机程序一样。从这个意义上讲，用于任何更专门的学习设置的任何学习算法也可以被视为在特殊类型的环境（例如环境）中运行的受限学习代理。监督学习环境可以通过训练阶段来定义，在该阶段中，环境为学习代理提供示例，然后在测试阶段中，环境对代理进行评估，最后是应用阶段，在该阶段中，实际使用经过训练和验证的模型。对于更具交互性的学习场景，例如强化驱动的学习模式RL，我们也很明显地做到这一点，我们在I.B.2节中对此进行了简要说明，它是在AE范式中使用的。换句话说，所有机器学习模型和设置都可以用广泛的AE范式表述。

  尽管AI的领域分为几个研究分支，专注于孤立的特定目标，但该领域的最终动机仍然是相同的：真正的通用AI的设计，有时也称为人工通用智能（AGI），即 ，设计“真正智能”的代理（Russell和Norvig，2009年）。

  建立AGI需要哪些成分是难以确定的，而且没有达成共识。 一种观点集中在代理的行为方面。 在文献中，智能行为的许多特征是通过表征更多特定类型的代理来捕获的：简单的代理，基于模型的代理，基于目标的代理，基于效用的代理等。每种类型都捕获了智能行为的一个方面，就像 ML领域的片段（被理解为AI的一部分）捕获了智能代理应处理的特定类型的问题。 就我们的目的而言，智能代理的最重要，最重要的方面是学习的能力，我们将特别强调学习代理。

  AE范例特别适合于这种操作角度，因为它从代理的内部结构中抽象出来，并着重于行为和输入-输出关系。 更准确地说，本篇综述中关于AI的观点相对简单。 a）AI适用于在其环境中进行智能行为的代理，并且b）智能行为的核心方面是学习。

  毫不奇怪，尽管我们没有更精确地指定智能行为的含义，但对AI的这种简单观点已经产生了不小的后果。 首先，可以仅从代理与其环境之间的交互历史确定智能。 这种关于AI的观点也与基于行为的AI和图灵测试背后的思想密切相关（Turing，1950）。 它与关于AI的具体观点是一致的（请参见I.B部分的具体AI），并且它影响了VII.C部分所涉及的量子AI的某些方法。 第二点是，更好的ML和其他类型的相关算法的开发确实构成了AI的真正进步，其前提是这样的算法可以连贯地组合成一个完整的代理。 但是，重要的是要注意，实际上实现这种集成可能并非易事。

  与严格的行为和操作观点相反，针对整个主体（或完整的智能主体）的另一种方法侧重于 主体架构和认知架构（Russell和Norvig，2009）。 在这种人工智能方法中，重点不仅放在智能行为上，而且在形成关于（人类）思想结构的理论上也同样如此。 认知体系结构的主要目标之一是设计一个综合的计算模型，该模型封装了来自认知心理学研究的各种结果。 然而，主要集中在理解人类认知的方面并不是我们对AI的关注。

  我们将在第VII.C节中进一步讨论。

C. 附录（ Miscellanea）

a. 缩写与首字母缩略词（ Abbreviations and acronyms）

b. 注解（ Notation ）

  在整篇审阅文件中，我们都努力使用审阅作品中指定的符号。 为避免符号混乱，我们在各小节中都使符号保持一致——这意味着在一个小节中，如果出现不一致之处，我们将遵循大多数作品中使用的符号。

Ⅱ 研究背景（ CLASSICAL BACKGROUND）

  本部分的主要目的是提供有关经典ML和AI技术的概念和背景，这些知识或概念将在以下各节中讨论的量子理论中有涉及，或者对于在更广泛的学习环境中正确定位量子位很重要。 本节的概念和模型包括经典文献中常见的模型，以及某些更奇特的模型，这些已在现代量子ML文献中得到解决。 尽管本节包含理解量子ML文献的基本思想和所需的大多数经典背景，但为了精简本节的篇幅，在即将进行的评论中，一些非常专业的经典ML思想也会详细讲解的。

  我们首先介绍与常见ML模型相关的基本概念，在II.A.1中介绍 神经网络，在II.A.2中介绍 支持向量机。 在此之后，在II.A.3中，我们还简要地描述了更多的算法方法，以及在ML上下文中产生的思想，包括 回归模型，k-均值/中位数，决策树， 以及更一般的线性优化模型， 现在在ML中很常见的代数方法。 除了学习问题的模型设计的更为实用的方面之外，在第二节B部分中，我们提供了 计算学习理论的数学基础 的主要思想，这些思想讨论了可学习性，即可以进行学习的根本条件，计算学习理论和 Vapnik和Chervonenkis的理论–严格研究各种监督环境下学习效率的界限。 II.C小节涵盖了 RL的基本概念和方法。

A. 机器学习方法（ Methods of machine learning）

小节摘要：机器学习中两个特别著名的模型是人工神经网络（受生物大脑的启发）和支持向量机（可以说是最能理解的监督学习模型）。神经网络有很多优点，所有这些都为简单的计算单元（神经元）网络的并行信息处理建模。前馈网络（无循环）通常用于监督学习。大多数流行的深度学习方法都适合这种范例。循环网络存在环路——这允许将信息从（子）网络的输出反馈回其自己的输入。例如，可以用作内容寻址存储器的 Hopfield网络，以及通常用于 无监督学习的Boltzmann机器。这些网络分别是零温度或有限温度下的相关Ising型模型，这为一些量化建议奠定了基础。支持向量机通过确定最佳的分离超平面来对欧几里得空间中的数据进行分类，从而获得了相对简单的理论。该模型的线性是使其能够进行量子处理的特征。超平面分类的功能可以通过使用内核来提高，这些内核可以直观地以非线性方式将数据映射到更高维的空间。 ML自然超越了这两个模型，并且包括回归（数据拟合）方法和许多其他专用算法。

  自从AI和ML领域出现以来，就如何实现我们上面介绍的学习方式有了很多相关研究。 接下来，我们将描述ML的两种流行模型，特定的 人工神经网络和支持向量机。 我们着重指出，存在许多其他模型，实际上，在许多领域中，更常使用其他学习方法（例如回归方法）。 此后简述这些其他模型的选择，以及在广义上与ML主题重叠的技术示例，例如矩阵分解技术，并且可用于无监督学习。

  我们的重点选择在某种程度上再次受到后来的量子方法和模型特征的推动，这些 模型特征特别适合于量子计算的交叉。

1. 人工神经网络和深度学习（ Artificial neural networks and deep learning）

  人工神经网络（简称人工NN或仅NN）是一种从生物学角度出发解决学习问题的方法。 始于1943年（McCulloch和Pitts，1943），神经网络的基本组成单元是人工神经元（AN），抽象而言，它是一个实值函数AN：R^k→R由实数，非负数的向量参数化 权重（w_i）_i = w∈R ^k，激活函数φ：R→R，表示为

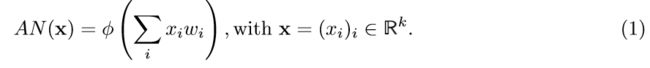
对于激活函数为阈值函数φθ（x）= 1（如果x>θ∈R +且φθ（x）= 0）的特殊选择，AN被称为感知器（Rosenblatt，1957年），并且已经进行了广泛的研究。这样的简单感知器已经将超平面指定的子空间分类为具有方向向量w和偏移θ的物体类别（参见本节后面的支持向量机）。

  请注意，在ML术语中，应区分人工神经元（AN）和感知器——感知器是AN的特殊情况，具有固定的激活函数（阶跃函数）和指定的更新或训练规则。现代的AN使用各种激活函数（通常是不同的S型函数），并且可以使用不同的学习规则。 就我们的目的而言，这种区别将无关紧要。为了监督学习而对此类分类器/ AN的训练包括优化参数w和θ以正确标记训练集有多种优点值得特别关注的方法，以及在执行这种优化的各种算法上不相关。通过将AN组合到网络中，我们可以得到NN（如果AN是感知器，那么我们通常谈论多层感知器）。 尽管单层感知器只能实现线性分类，但已经有一个三层网络成功地逼近了任何连续的实值函数（精度取决于内部所谓的“隐藏”层中的神经元数量）。Cybenko（Cybenko，1989）是第一个证明sigmoid 激活函数的方法，而Hornik对此进行了概括，以表明此后不久，所有非恒定，单调增加且有界的激活函数也是如此（Hornik，1991）。 这表明，如果有足够多的神经元可用，原则上可以训练三层ANN学习任何数据集。尽管这个结果看起来很完美，但是它伴随着一个复杂模型的代价，我们将在II.B.218节中讨论。近年来，很明显，使用多个顺序的，隐藏的前馈层（而不是一个较大的），即 深度神经网络（深度NN），可能会有更多好处。首先，它们可以 减少参数的数量（Poggio et al。，2017）。其次，可以 将信息从层到层的处理的顺序性质理解为特征抽象机制（每一层对输入进行一点处理，突出显示要进一步处理的相关特征）。这 增加了模型的可解释性（直观上是对模型性能进行高级解释的能力）（Lipton，2016），这也许最好用所谓的卷积（深）NN来说明，其结构是受视觉皮层启发的 。这种深度网络的主要实际 缺点之一是训练中的计算成本和计算不稳定性（参见消失的梯度问题（Hochreiter等人，2001）），而且 数据集的大小也必须很大（Larochelle） 等（2009）。 随着现代技术和数据集的出现，这两个障碍变得越来越难以接受，这导致了机器学习领域的一次小革命。

  并非所有的ANN都是前馈的：递归神经网络（递归NN）允许信号的反向传播。 这种网络的特殊示例是所谓的 Hopfield网络（HN）和Boltzmann机器（BM） ，它们通常与前馈网络用于不同的任务。在HN中，我们处理一层，其中所有神经元的输出充当同一层的输入。 通过为神经元分配二进制值（传统上，为方便起见，使用-1和1）来初始化网络（更确切地说，将某些神经元设置为火，而另一些不设置为火），然后由网络对其进行处理， 导致了新的配置。此更新可以是 同步的（输出值是“冻结的”，并且所有第二轮的值是同时计算的），也可以是 异步的（更新是一次随机地以一个神经元进行的）。 网络中的连接由权重（wij）ij矩阵表示，该矩阵指定了第i个神经元和第j个神经元之间的连接强度。神经元是具有阈值激活功能的感知器，具有局部阈值矢量（θi）i。 在一些温和的假设下（Hopfield，1982），这样的动力系统收敛到一个配置（即位串），该配置（局部）使能量功能 最小化。

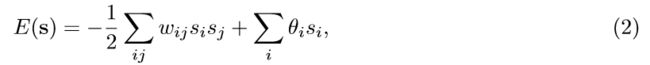
s =（s_i）_i，s_i∈{−1,1}，即Ising模型。 通常，此模型具有许多局部最小值，这取决于权重wij和阈值（通常设置为零）。 Hopfield提供了一种简单的算法（出于历史原因，在D. Hebb之后被称为Hebbian学习（Hopfield，1982）），它使一个人可以“编程”最小值，换句话说，给出了一组位串S（更确切地说，是 符号+ 1 / -1），则可以找到矩阵w_ij，以使这些字符串S恰好是所得函数E的局部最小值。 这样的编程最小值然后称为存储模式。 此外，Hopfield的算法以 局部方式（权重wij仅取决于目标字符串的第i位和第j位，允许并行化），增量方式（可以修改矩阵wij以添加新字符串而无需保留）来实现内存中的旧字符串的目的 ，并且立即执行。 即时性意味着权重矩阵的计算不是限制性的，而是有限的过程。违反例如 增量性将导致惰性算法（请参阅I.B.3节），该算法在内存需求方面可能不是最优的，但在计算复杂性上也不是很小。结果表明，这种训练有素的网络的最小值也是吸引点，具有有限的吸引力。这意味着，如果将经过训练的网络馈入新的字符串，并让其运行，它将（最终）收敛到最接近它的模式（所使用的距离度量取决于学习规则，但通常是Hamming 距离，即字符串不一致的条目数）。这样的系统然后形成 关联存储器，也称为内容可寻址存储器（CAM） 。 CAM可以用于监督学习（“标签”是存储的模式），反过来，监督学习机制可以用于CAM。 HN的一个重要特征是它们的容量：它可以存储多少种不同的模式。 对于Hebbian更新规则，此数字的缩放比例为O（n / log（n）），其中n是神经元的数量，Storkey（Storkey，1997）将其改进为O（n / √log(n))。同时，已经研究出了更有效的学习算法（Hillar和Tran，2014）。

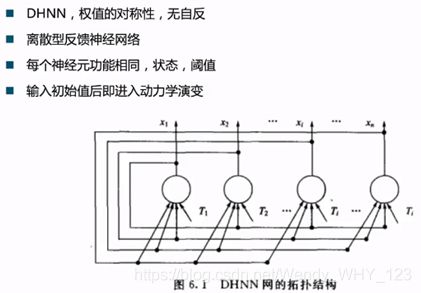
   除了作为CAM的应用之外，由于等式中能量功能的表示形式（2），以及HN的运行将其最小化的事实，它们也早已被考虑用于优化任务（Hopfield和Tank，1985年）。从技术上讲，Hopfield网络与Ising模型之间的有效同构仅在零温度系统的情况下成立。 Boltzmann机器对此进行了概括。 在此，第i个神经元的值被设置为-1或1（在文献中分别称为“ off”和“ on”）

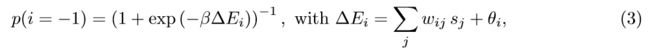
其中∆Ei是第i个神经元在或在off配置时的能量差，假设连接w是对称的，而β是系统的逆温度。在无限运行时间的情况下，网络的配置由配置上的（输入状态不变）Boltzmann分布给出，这取决于权重w，局部阈值（权重）θ和温度。BM通常以生成方式 使用，以从（条件）概率分布中建模和采样。 在最简单的变体中，网络的训练试图确保网络的极限分布与数据集中观察到的频率匹配。 这是通过调整参数w和θ来实现的。 网络的结构决定了分布的复杂程度。 为了捕获更复杂的分布，例如说k维数据，BM具有N> k个神经元。其中k个表示为可见单元，其余的称为隐藏单元，它们捕获生成数据集的系统（实际上是我们正在建模）的潜在变量，而不是直接可见变量。 训练这样的网络包括在参数空间中观察训练数据的对数似然的梯度上升。尽管从概念上讲这似乎很简单，但它在计算上很棘手，部分原因是它需要精确估计平衡分布的概率，而这很难获得。 实际上，通过使用受限BM可以在某种程度上缓解这种情况，其中隐藏和可见单元构成了二部图的分区（因此仅存在隐藏和可见单元之间的连接）。 （受限制的）BM具有广泛的用途，包括提供生成模型-从估计的分布中生成新样本，作为分类器-通过条件生成，作为特征提取器-无监督聚类的一种形式，以及作为深层结构的组成部分。 但是，它们的效用主要受到训练成本的限制，例如，获得平衡吉布斯分布的成本，或者受启发式训练方法（例如对比发散）产生的误差的限制。

2. 支持向量机（Support Vector Machines）

  支持向量机（SVM）构成了解决分类问题最容易理解的一类方法。 SVM的基本思想是，对于二进制标签y_i∈{-1,1}，基于数据集{x_i，y_i}_ i对点进行分类的自然方法是生成一个将负实例与正实例分离的超平面。 这样的观察并不新鲜，实际上，在上一节中讨论的感知器执行相同的功能。

  然后可以使用这种超平面对所有点进行分类。 自然地，并不是所有的点集都允许这样做（可以这样分类的点被称为线性可分离），但是支持向量机进一步一般化以处理所谓的不能线性分离的集合。 内核有效地实现了原始数据集到更高维度的非线性映射，这些映射可能会变得分离，这取决于一些技术条件 ），并允许一定程度的错误分类，这导致了所谓的“软边际” SVM。

  即使在数据集是线性可分离的情况下，仍然会有许多超平面完成这项工作。 这导致了SVM的各种变体，但是基本变体标识了一个超平面：a）正确地分割训练点，b）最大化所谓的余量：超平面到最近点的距离（见图7）。

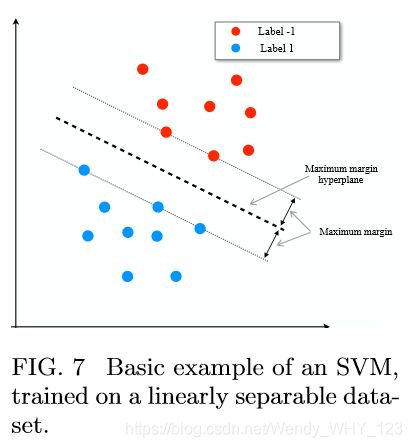
  这里使用的距离通常是 几何欧几里得距离，这导致所谓的最大余量分类器。 在高维空间中，通常，在有多个+1和-1训练数据点实例与超平面距离相等的情况下，边界的最大化结束。 这些点称为支持向量。 寻找最大余量分类器对应于寻找法向量w和分离超平面的偏移b，这对应于优化问题

上面的公式实际上是从基本问题中得出的，要注意的是，我们可以在不更改超平面的情况下任意同时缩放该对（w，b）。 因此，我们总是可以选择一个缩放比例，以使实现的余量为1，在这种情况下，余量对应于||w||^-1，这如上所述将一个最大化问题映射到一个最小化问题。 平方确保问题被陈述为标准二次规划问题。 此问题通常以Lagrange对偶形式表示，可简化为

换句话说，我们已经根据数据向量表示了w*，并且对应系数αi不为零的数据向量xi就是支持向量。 通过求解w* .x^+ + b*= 1，可以容易地计算出偏差b*，从而可以访问一个表示为x +的实例+1的支持向量。也可以使用支持向量通过以下表达式直接计算新点z的类别

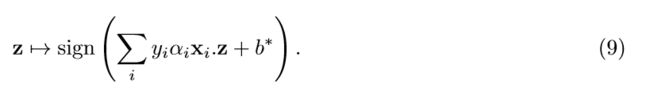
当处理内核时，优化问题的双重表示很方便。 如上所述， 处理不可线性分离的数据的方法是，首先通过非线性函数φ：Rm→Rn将所有点映射到更高维的空间，其中m 如我们所见，在对偶表述中，数据点仅以内积xi.xj的形式出现。 这导致了核函数k的概念，该函数直观地测量较大空间中的点的相似性，通常用k（x_i，x_j）=φ（x_i）Tφ（x_j）定义。 换句话说，为了根据由非线性映射φ引起的非平凡核k训练SVM，优化等式（6）替换为argminα1…α(Σ_i α_i− 1 2Σ_i,j(α_iα_jy_iy_jk（x_i，x_j)）。仅使用φ的一个应用类似地计算该偏移量。 用z →sign（Σ_i(y_iα_ik（x_i，z）+ b *）)以相同的方式给出新点的评估。换句话说，只要可以更有效地计算出映射的内积k（·，·），就不需要通过φ来明确映射数据点。 内核的选择对分类器的性能至关重要，而好的内核的发现并非易事，并且常常通过反复试验来解决。

  虽然增加扩展空间的尺寸（φ的共域）可能会使数据点更线性地分离（即，最佳分类器的失配更少），但实际上它们将无法完全分离（此外，增加内核尺寸 费用，我们稍后会详细说明）。 为了解决这个问题，SVM支持分类错误，并提供了各种选项来测量分类错误的“数量”，从而产生 惩罚函数。 一种典型的解决方案是在原始优化任务中引入所谓的“松弛变量”ξi≥0， 因此：

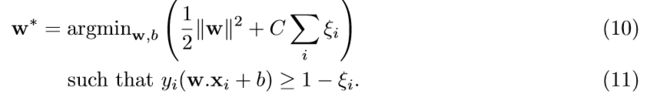
如果最优解的值ξi在0到1之间，则将点i正确分类，但在边距之内，并且ξi> 1表示错误分类。（超）参数C控制着我们在保证最小化范数上的相对重要性，以及我们在分类错误上的重要性。有趣的是，上述问题的双重表述与到目前为止讨论的硬边际设置几乎相同，不同之处在于参数αi现在在等式中受αi≤C的约束（7）。如上所述，从计算学习理论的角度对SVM进行了广泛的研究，并将其与其他学习模型相连接。 特别是可以粗略地描述表征训练模型在训练集之外的表现的概括性能（即模型的泛化能力）。这是分类算法的最重要特征。 我们将在第二节B.2中简要讨论泛化性能。 我们通过考虑非标准变体来结束对SVM的简短回顾，这对于我们的目的很有趣，因为它已经被证明有利于量化。通过找到最大余量超平面来训练所描述的SVM。 另一种称为 最小二乘支持向量机（LS-SVM） 的模型采用了一种回归（即数据拟合）方法来解决该问题，并找到了一个超平面，该超平面实质上使标签向量之间的最小平方距离最小。 其中距超平面的距离向量的第i个条目由（w.xi + b）给出。 这可以通过对软边际公式进行小的修改来实现：

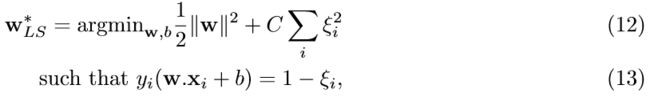
两个模型的两个主要区别是约束的改变，LS-SVM中的约束时相等的，松弛变量在优化表达式中平方。 这种看似简单的变化会导致训练和性能差异。 后一个优化问题的对偶表示简化为一个线性方程组：

其中1是“全1”向量，Y表示标签y_i的向量，b表示偏差，γ取决于C的参数。α是拉格朗日乘数的向量，它得出解。 这个向量再次由于空间限制而被我们省略的对偶问题可以在（Suykens和Vandewalle，1999）中找到。 最后，Ω是收集训练向量的（映射的）“内积”的矩阵，因此Ωi，j = k（xi，xj），其中k是核函数，在最简单的情况下，仅是内积。 因此，LS-SVM的训练更简单（从量子算法的角度来看特别方便），但是对模型的理论理解以及它与易于理解的SVM的关系仍然是需要研究的问题，很少有已知结果（ 参见例如（Ye and Xiong，2007）。

3. 其他模型（Other models）

  尽管NN和SVM是ML任务（特别是监督学习）的两种主流方法，但还存在许多其他模型，适用于各种ML问题。 在这里，我们非常简短地列出并描述了一些这样的模型，它们也出现在量子ML的背景下。 虽然分类通常为点分配离散的标签，但在标签函数具有连续域（例如段[0,1]）的情况下，我们正在处理函数逼近任务，通常使用回归技术来处理。此处的典型示例包括线性回归，该线性回归使用线性函数近似点和标签之间的关系，通常将最小二乘误差最小化。 更广泛地讲，此类技术与 数据拟合 密切相关，也就是说，拟合参数化函数的参数，例如最适合观察（训练）数据。k最近邻算法 是一种直观的分类算法，它给定一个点，考虑k个最近的训练点（相对于选择的度量标准），并通过多数表决（如果用于分类）或通过平均分配标签 （在回归的情况下，即连续的标签值）。 相互关联的k均值和k均值算法通常用于聚类：k指定聚类的数量，该算法以最小化聚类内到均值（或中位数）距离的方式定义它们。

  分类和回归的另一种方法是 优化决策树，其中每个维度或新数据点的条目（或更一般地说是特征）都会影响决策树的移动。 树的深度是特征数量，每个节点的程度取决于每个条目可能存在的不同特征/级别的数量。 树的顶点指定了感兴趣的任意特征，这可能会影响分类结果，但大多数情况下，它们会考虑与数据点空间的几何区域重叠。 决策树理论上具有最大的表达能力（可以表示任何标记功能），但是很难进行约束训练。

  更一般而言，分类任务可以看作是找到假设h：数据→标签（在ML中，假设是术语分类者的同义词，也称为学习者），该术语来自某个族H，在某些损失函数下，可以最大程度地减少错误（或损失）。例如，由SVM实现的假设由超平面给出（在内核空间中），而在神经网络中，它们由网络的参数进行参数化：几何，阈值，激活函数等。除了损失项最小化之外，其中ML被称为经验风险最小化，ML应用受益于在目标函数中添加附加组件：***正则化项，其目的是对复杂函数进行惩罚，***否则可能导致不良的泛化性能，请参阅第II.B节。损失函数，正则项和假设类别的选择会导致形成不同的特定模型，并且训练对应于损失函数和假设（函数）族的选择所带来的优化问题。 此外，已经表明，基本上任何仅需要凸优化训练的学习算法都会导致噪声下的较差性能。因此，非凸优化对于最佳学习是必不可少的（例如参见（Long and Servedio，2010; Manwani and Sastry，2011））。

  分类问题的重要一类元算法是 增强算法。 Boosting算法背后的基本思想是高度非平凡的观察，这是通过具有开创性的AdaBoost算法（Freund和Schapire，1997年）首次证明的，可以 组合多个弱分类器，它们在输入空间的不同部分上的表现要好于随机性。 成为整体上更好的分类器。更准确地说，给定一组（弱）假设/分类器{h_j}，h_j：Rn→{−1,1}，在某些技术条件下，存在一组权重{w_i}，w_i∈R，使得 hc_w（x）= sign（Σ_i (w_ih_i（x）)）形式的复合分类器效果更好。有趣的是，可以使用单个（弱）学习模型来生成构建更好的复合分类器。所需的弱假设从原理上讲，可以实现任意的高成功概率，即强学习者。 此过程的第一步是通过 更改训练标记的数据点出现的频率来实现 的，可以有效地更改数据的分布（在黑盒设置中，可以通过例如拒绝采样方法获得这些分布）。 在这样的差异分布的数据集上训练一个相同的模型会产生不同的弱学习者，这些弱学习者会强调输入空间的不同部分。 一旦产生了这些不同的假设，就对复合模型的权重进行优化。 换句话说，弱学习模型可以得到加强。

  除了用于解决各种ML任务的方法之外，ML还经常与用于解决这些问题的特定计算工具混为一谈。一个突出的例子是优化问题算法的开发，尤其是在标准学习模型训练中出现的算法。这包括 粒子群优化，遗传进化算法，甚至是随机梯度下降的变体。 ML还依赖于其他方法，包括线性代数工具，例如矩阵分解方法（例如奇异值分解，QR-，LU-和其他分解），派生方法（例如主成分分析）和信号分析领域的各种技术（傅立叶，小波，余弦和其他变换）。后一组技术可用来减少数据集的有效维度，并有助于消除维度的诅咒。优化，线性代数和信号处理技术以及它们与量子信息的相互作用是一个独立的研究机构，具有足够的材料值得单独审查，我们将仅在需要时对这些方法进行反思。

B. 监督学习和归纳学习的数学理论（ Mathematical theories of supervised and inductive learning）

执行摘要：除了提出诸如NN或SVM之类的学习模型外，学习理论还提供了识别可学习性限制的正式工具。 没有免费的午餐 定理提供清醒的论点，即无法获得“最优”学习模型的朴素概念，并且 所有学习都必须依赖一些先前的假设。计算学习理论依靠来自计算复杂性理论的思想来形式化许多监督学习的设置，例如 近似或识别未知（布尔）函数（一个概念）的任务，该概念只是二进制标记函数。该理论的主要问题是 量化黑匣子（即函数（或提供所选输入的函数值示例的oracle）的调用）的数量，以可靠地近似（部分）未知概念 达到所需的精度。换句话说，计算学习理论考虑了各种学习设置的样本复杂性界限，指定了概念族和访问类型。Vapnik和Chervonenkis的理论（简称 VC理论）源于统计学习的传统。 该理论的主要目标之一是 为泛化性能提供理论上的保证。 这就是以下问题的要求：给定一个学习机在大小为N的数据集上进行训练，该数据源来自某个过程，并且测得的经验风险（训练集上的误差）为某个值R，可以说 它在其他数据点上的未来性能可能源自同一过程？ VC理论的主要结果之一是，这可以借助第三个参数（学习机的模型复杂性）得到解答。模型的复杂性直观地反映了学习者可以学习的复杂功能：模型越复杂，“过度拟合”的机会就越大，因此，超出训练集的性能保证就越弱。 好的学习模型可以控制模型的复杂性，从而导致结构风险最小化的学习原理。 机器学习的技巧是一种类似杂耍的行为，它平衡了样本复杂度，模型复杂度和学习算法的计算复杂度。

  尽管现代对ML和AI的兴趣增加主要是由于应用程序，但ML和AI的各个方面确实具有强大的理论背景。 在这里，我们关注于这样的基础性结果，这些结果阐明了什么是学习，并且调查了限制学习的问题是什么。 我们将简要介绍一些基本思想。

  第一个结果集合称为“无免费午餐定理”，这似乎对所有可能的学习条件都抱有悲观的界限（Wolpert，1996）。 从根本上说，没有免费的午餐定理是Hume著名的 归纳问题（休H，1739；维克斯，2016）的数学形式化，它涉及归纳推理的合理性。 归纳推理的一个例子发生在泛化过程中。 Hume指出，在没有先验假设的情况下，基于任何数量的观察结果得出与一类物体有关的任何概念都是没有道理的。

  同样，在没有进一步假设的情况下，基于经验的学习是无可辩驳的：如果假设自然界的统一性，则期望一系列事件会导致与过去相同的结果是合理的。泛化和统一性问题可以在监督学习和RL的背景下提出，其后果（并非毫无争议）会引起影响（参见（NFL））。例如，含义之一是，如果一个训练算法对所有可能的标记函数进行均值平均，并且类似的语句适用于RL设置，则除训练集之外的任何两种学习算法的预期性能必须相等。换句话说，无需假设在环境/数据集上，任何两个学习模型的预期性能将基本相同，并且如果不对所讨论的任务环境做出陈述，就无法在性能方面对两个学习模型进行有意义的比较。但是，实际上，我们总是对数据集和环境有一些假设：例如， 简约性原理（即奥卡姆剃刀） ，断言 更简单的解释往往是正确的，在科学中盛行，成功打破了NFL所需的对称性。保持最坚强的形式（Lattimore和Hutter，2011； Hutter，2010； Ben-David等，2011）。

  对学习理论的理论基础的任何评论都不应绕过Valiant的著作，而通用计算学习理论（CLT）则源于Valiant（Valiant，1984）发起的计算机科学传统以及相关的Vapnik和VC的VC理论。 Chervonenkis，是从统计学的角度发展起来的（Vapnik，1995）。 我们以不特定的顺序介绍了这些理论的基本思想。

1. 计算学习理论（Computational learning theory）

  CLT可以理解为监督学习的严格形式化，它源于计算复杂性理论。 CLT中最著名的模型是近似正确（probably approximately correct，PAC）学习模型。 我们将通过一个简单的示例来解释PAC学习的基本概念：字符识别。 考虑训练算法的任务，方法是提供一组示例和反例：一组图像，从而确定一个字母的给定图像（以黑白位图表示）是否对应于字母“ A”。 每个图像x可以被编码为{0,1}^n中的二进制矢量（其中n =高度×图像宽度）。假设每个图像都唯一正确地分配了标签0（不是“ A”）和1，则意味着存在一个特征函数f：{0,1} n→{0,1}，可以从其他图像中识别出字母A。 在计算学习理论中，这种潜在的特征函数（或等效地，为其达到值“ 1”的位串的子集）称为概念。 首先，将向所有（监督）学习算法提供N个示例（xi，f（（xi））i）的集合。在PAC学习的某些变体中，假定数据点（x）是从某种分布中得出的 D达到{0,1} n中的值。从直觉上讲，这种分布可以模拟这样一个事实：在实践中，提供给学习者的例子源于其与世界的互动，后者指明了我们更可能看到哪种“ A” 。 PAC学习通常采用归纳设置，这意味着在给定样本集SN（包含来自D的N个相同独立分布的样本）的情况下，学习算法会输出假设h：{0,1} n→{0,1} 算法对实际概念“最佳猜测”。 猜测的质量由总误差（也称为损失或遗憾）来衡量。

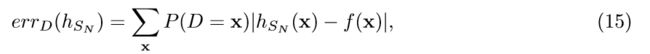
根据相同的（训练）分布D进行平均，其中hSN是假设（给定训练集SN）（确定性）学习算法输出的假设。 直观地讲，训练集（N）越大，误差将越小，但这也取决于实际示例（并因此取决于SN和D）。 PAC理论涉及（δ）个，大约（∈个）正确的学习，即以下表达式：

其中S〜D表示根据分布D绘制S。上面的表达式是一个证明，该学习算法已经对从D采样的数据集进行了训练，除概率δ外，总误差低于。 我们说，如果存在学习算法，则在分布D下，概念f是（∈，δ）可学习的，如果存在学习算法，则N是等式。 （16）成立，并且对于所有（∈，δ）选择都是（∈，δ）可学习的，就可以简单地学习。N对（∈，δ）（以及概念和分布D）的函数依赖性称为样本复杂度。 在PAC学习中，我们主要关注确定难解决的问题，因此，如果存在一个样本/复杂度对-1和δ-1为多项式的算法，则概念/分布对f，D是PAC可学习的。 这些基本思想可以通过多种方式概括。 首先，在算法无法输出所有可能的假设而仅输出受限集合H的情况下（例如，假设空间小于总概念空间），我们可以通过将实际概念f替换为最优来寻找最佳情况解决方案 在上述所有表达式中，选择h*∈H可使（15）中的误差最小。其次，我们通常不希望仅将字母“ A”与所有其他字母区分开，而是要识别所有字母。 从这个意义上讲，我们通常处理概念类（例如“字母”），它是一组概念，如果存在该类中每个概念都为（PAC）的算法，则它是（PAC）可以学习的。 此外，如果相同算法也为所有分布D学习，则该类被称为（自由分布）可学习。

  CLT包含其他模型，概括了PAC。 例如，概念可能是有噪声的或随机的。 在 不可知论学习模型 中，从{0,1} n×{0,1}上的分布D抽取有标记的示例（x，y），这也对概率概念进行了建模。 此外，在不可知论学习中，我们定义了一组概念C⊆{c | c：{0,1} n→{0,1}}，并且在给定D的情况下，我们可以确定集合C中D的最佳确定性近似 ，由optC =minc∈CerrD（c）给出。 学习的目标是产生一个假设h∈C，在PAC的意义上，该假设的表现不比最佳逼近optC差很多–如果可以访问样本，该算法是D和C的（∈，δ）-不可知学习者 从D出发，输出假设h∈C，使得errD（c）≤∈+ optC（概率δ除外）。

  CLT中的另一个常见模型是，从 成员资格查询模型中进行精确学习（Angluin，1988），从直觉上讲，它与主动监督学习有关（请参阅第I.B.3节）。 在这里，我们可以访问一个预言家，一个黑盒子，当用示例x查询时，它会输出概念值f（x）。 基本设置是精确的，这意味着我们需要输出一个假设，该假设不会有任何错误，但是有一定的可能性（例如3/4）。 换句话说，这是PAC学习，其中∈= 0，但是我们可以选择自适应地给出哪些示例，并且δ的范围是1/2。 在这种情况下，通常考虑的绩效指标是 查询复杂度，它表示学习算法使用的对oracle的调用次数，并且在大多数情况下都与样本复杂度同义。 从本质上讲，这对应于主动的有监督学习环境。

  PAC的许多学习都涉及识别有趣的概念类的示例，这些概念类是可学习的（或证明相关类不可行），但是存在其他更普遍的结果，可以连接该学习框架。 例如，我们可以问我们是否可以实现有限采样的通用学习算法：即可以使用一定数量的样本N在任何分布下学习任何概念的算法。我们前面提到的“免费午餐”定理暗示： 这是不可能的：对于每种学习算法（∈，δ），任何N都有一个设置（概念/分布），需要超过N个样本才能实现（∈，δ）学习。

  通常，解决问题的标准是假设存在一个分类器，该分类器的性能基本上是任意的，即，假设该分类器的性能很强。 在II.A.3节中已经提到的ML的提升结果表明，对弱分类器的适应（其性能仅比随机分类略好）不会产生可学习性的不同概念（Schapire，1990）。

  古典的 CLT理论也已被推广来处理连续范围的概念。 特别地，所谓的p概念的范围是[0,1]（Kearns和Schapire，1994）。 整个CLT的泛化以处理此类连续值的概念并非没有问题，但是尽管如此，一些中心结果（例如与VC维类似的数量以及与泛化性能相关的类似定理）仍可以提供（参见（Aaronson，2007年）有关在VA1节中讨论的量子态学习中的概述）。

  计算学习理论与Vapnik和Chervonenkis的统计学习理论（VC理论）密切相关，我们将在后面进行讨论。

2. VC维理论（VC theory）

  Vapnik和Chervonenkis的统计学习形式主义是在30多年的过程中发展起来的，在这篇综述中，我们仅介绍总体理论中选定的一个方面，该理论涉及 保证泛化性能。 在上一节有关PAC学习的段落中，我们介绍了总误差的概念，我们将其称为（总）风险。它定义为所有数据点的平均值，对于假设h，假设R（h）= error（h）= Σ_x P（D = x）| h（x）- f（x）| （我们正在转换符号，以与不同文献保持一致）。 但是，在实践中无法评估此数量，因为在实践中我们只能访问训练数据。 这使我们想到了给定的经验风险的概念。

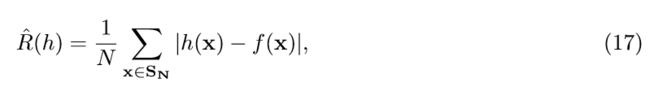
其中S_N是独立于基础分布D的训练集。

  ˆ R（h）的数量是直观且可直接测量的。 然而，发现仅靠经验风险优化学习模型的问题本身就并不能引起人们的兴趣，因为它可以通过查找表轻松解决。从学习的角度来看，更有趣和更相关的数量是超出训练集的性能，它包含在不可衡量的R（h）中，并且实际上归纳监督学习的任务是从有限训练集S_N识别使R（h）最小的h。从直觉上讲，最小化经验风险的假设h也应该是我们最小化R（h）的假设的最佳选择，但这只有在我们的假设族受到某种约束（至少限于总功能族）的情况下才有意义。查找表的经验风险为零，但对于超出范围的操作却一概不知。VC理论的主要贡献之一是在可观察量ˆ R（h）（经验风险），我们实际希望学习算法可以实现约束的R（h）量（总风险）与假设族之间建立严格的关系。直观地讲，如果函数族过于灵活（就像查找表一样），那么对示例的完美拟合就没什么用。相比之下，假设只有一组非常严格的假设（与数据集/概念和生成分布无关），则表明经验风险是对总风险的合理估计（但是可能很糟糕）， 因为没有为训练集量身定制任何内容。 这使我们想到了学习模型的模型复杂性的概念，该模型具有一些形式，在这里，我们关注模型的Vapnik-Chervonenkis维度（VC维度）。

  VC维是分配给一组假设H⊆{h | h：S→{0,1}}的整数（例如，原则上甚至可以训练我们的学习算法实现的可能的分类函数），例如，其中 S可以是位串{0,1} n的集合，或更一般地说，可以是Rn中的实向量。 在基本支持向量机的情况下，假设集为“所有超平面” 。现在考虑一般位置Rn中k个点的子集Ck。 这些点可以以2^k种不同的方式获得二进制标签。 假设族H破坏了集合C，如果对于集合C_k的任何标记 ，都存在一个假设h∈H，正确标记集合C_k。 换句话说，使用H中的函数，我们可以在一般位置上完美地学习k个点的集合Ck上的任何标记函数。H的VC维则是最大的k-max，因此，在一般位置上存在点的C_k_max集，该点被H粉碎（对于任何标记来说都是“可标记的”）。例如，对于n = 2，“射线”粉碎了三个 点而不是4个点（正方形的想象顶点，其中对角相对的顶点共享相同的标签），并且在n = N中，“超平面”粉碎N + 1个点。 尽管认为VC维与指定假设族的自由参数的数量相对应是令人困惑的，但事实并非如此。 VC定理（在其变体中的一种）（Devroye等人，1996）然后指出，经验风险与总风险相匹配，直至偏差不断扩大，样本数量在下降，但在模型的VC维数上却在增加 ，更正式地：

其中d是模型的VC维,N个样本， hSN是在给定训练集SN下模型的假设输出，这是从基础分布D采样的。基本分布D也隐式地出现在总风险R中。请注意，选择的可接受的错误率由真实错误率所限制（即概率δ）对数估计仅对数贡献∈，而VC维和样本数∈对的平方线性地（相互成反比）。

  VC定理表明，理想的学习算法应具有较低的VC维度（可以很好地估计经验风险和总风险之间的关系），同时在训练集上表现良好。 这导致了一种称为“结构风险最小化”的学习原理。 考虑一个参数化的学习模型（例如，由一个整数l∈l来参数化），这样每个l都会引发一个假设族H1，每个假设族H1的表现力都属于下一个假设H1 ⊆ Hl + 1。结构风险最小化（与将经验风险最小化的经验风险最小化相反）考虑到，为了拥有（保证）良好的泛化性能，我们既需要具有良好的观察性能（即 低经验风险）又需要具有 低模型复杂性。较高的模型复杂度会由问题结构风险引起，这种风险表现在常见问题中，例如数据过度拟合。在实践中，这是通过考虑参数化模型（例如{Hl}）来实现的，其中我们将l（影响VC维度）和与Hl相关的经验风险的组合最小化。实际上，这是通过 在训练优化中添加正则项 实现的，因此一般将导致argminh∈Hˆ R（h）的（非正规）学习过程更新为argminhl∈Hlˆ R（h）+ reg（l ），其中reg（·）惩罚假设族或给定假设的复杂性。

  VC维度在PAC学习中也是一个至关重要的概念，它将两个框架联系在一起。 首先请注意，概念集C（它是一组概念）也是一组合法的假设，因此具有明确的VC维d_C。然后，用O（dC + ln1 /δ）∈-1给出C的（∈，δ）-（PAC）学习的样本复杂度。

  上面的许多结果也可以在无监督学习的情况下应用，但是无监督（或结构学习）的理论主要与特定方法的理解有关，其主题超出了本文的范围。

C. 强化学习的基本方法和理论（ Basic methods and theory of reinforcement learning）

执行摘要：虽然RL通常研究 交互式 任务环境中的学习，但也许最好的理解模型会考虑更严格的设置。环境通常可以通过马尔可夫决策过程（Markov Decision Process,MDP）来表征，即它们可以由代理观察到。代理可以通过其动作引起从一个状态到另一个状态的转换，但是转换规则事先未知。 一些转换是有奖励的。在环境处于某种状态的情况下，代理可以学习执行哪些操作，以便在固定的时间范围内（有限的水平）或在较长的时间段内（渐近）获得最高的回报（预期回报） ，在无限水平下，未来的奖励在几何上可能会贬值。可以通过估计 动作值函数 来解决此类模型，该函数将预期收益分配给给定状态的动作，对于该状态，必须探索策略的空间，但是存在其他方法。在更一般的模型中，环境状态不需要完全可观察，并且这样的设置很难解决。RL设置也可以通过受物理随机过程启发的所谓投影模拟（Projective Simulation）框架中的模型来解决，这些模型用于设计学习代理。 尽管此模型相对较新，但它特别受关注，因为它在设计时就考虑了量化的可能性。交互式学习方法包括超出教科书的RL模型，包括部分可观察的设置，这需要泛化等等。 这样的扩展名，例如 一般化，通常需要非交互式学习场景中的技术，但也导致代理的自治程度不断提高。 从这个意义上讲，RL构成了ML模型与通用AI模型之间的桥梁。

  从广义上讲，RL处理学习如何在未知环境中表现最佳的问题。 在基本的教科书形式主义中，我们处理任务环境，这是由马尔可夫决策过程（MDP）指定的。 MDP是带有附加结构的带标记的有向图，包括离散的有限状态集S = {si}和动作A = {ai}，它们分别表示环境的可能状态以及学习代理可以在其上执行的动作 。

   代理动作的选择以特定于环境（MDP）的方式改变环境状态，并且是概率性的。 如果已经在状态s0中执行了动作a，则由转换规则P（s | s0，a）捕获，表示环境在状态s中结束的可能性。 从技术上讲，这可以看作是特定于动作的马尔可夫转移矩阵{Pa}a∈A的集合，学习者可以通过执行动作将其应用于环境。

  这些描述了以代理的行为为条件的环境动态。 指定环境的最终组件是奖励函数R：S×A×S→Λ，其中Λ是一组奖励，通常为二进制。 换句话说，环境会奖励某些转变。 在每个时间点，学习者的行为都由以下策略指定： 条件概率分布 π(a|s) ，指定条件是主体处于状态s时代理输出行为a的概率。 在给定MDP的情况下，直观地讲，目标是找到良好的政策，即产生高回报的政策。 这可以用许多非等效的方式来形式化。

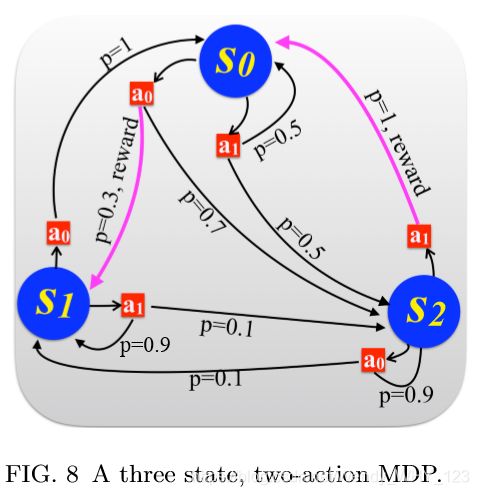
  给定一个策略π和一些初始状态s，我们可以 在Rs N（π）= ΣN i = 1（ ri）的N个交互步骤之后，定义有限水平的期望总回报，其中ri是在给定环境中，假设我们从 状态s出发，策略π在时间i时的期望回报。如果环境是有限且紧密相连的，则随着水平N的增长，有限水平的回报也会不同。 但是，通过添加 几何折旧系数（比率γ） ，我们得到了一个始终有界的表达式Rγ（π）=Σ∞i = 1(γiri)，称为无限地平线期望奖励（由γ参数化），这在文献中更为常见。 在 有限或有限的范围内预期获得的回报是解决MDP问题的典型绩效指标。它表现在两个方面。 首先，在决策理论或计划中（在AI的背景下），典型的目标是找到一种优化策略π，该策略正式优化给定MDP中（有限）地平线奖励的形式：给定（全部或部分）规范 MDP，求解πopt=argmaxπRN/γ（π），其中R分别是有限（对于N步）或有限水平（对于给定的折旧γ）设置中的预期收益。这些问题可以通过动态和线性编程来解决。 相比之下，在RL（Sutton和Barto，1998）中，没有给出环境（MDP）的规范，而是可以通过与之动态交互来探索。 代理可以执行一个动作，并接收后续状态（也许是奖励）。 这里的最终目标来自两个相关（但在概念上不同）的风味。 一种是设计一个代理，该代理将随着时间的推移学习最佳策略πopt，这意味着可以从代理/程序的内存中读取该策略。 我们稍有不同，我们希望一个代理随着时间的推移逐渐改变其行为（政策），使其按照最佳政策行事。 从理论上讲，这两个是密切相关的，例如 在机器人技术中，这些是非常不同的，因为收敛（完美学习）之前的奖励率也很重要。首先，我们指出，只要MDP有限且紧密连接，就可以可靠地解决上述RL问题：一个简单的解决方案是坚持随机策略，直到可以对环境进行可靠的层析成像为止，然后 问题是通过动态编程来解决的。39.通常，环境实际上具有附加的结构，即所谓的初始状态和终端状态：如果代理到达终端状态，则将其“传送”到固定的初始状态。 这种结构称为情景结构，可以用作确保MDP强大连接的一种手段。【注：MDP是需要给出环境的规范和奖励机制的，但是RL没有；又称为有模型的无模型的学习方法】

  获得解决方案的一种方法是通过跟踪所谓的值函数Vπ（s）：S→R，假设我们从状态s开始，它们在策略π下分配期望的报酬； 这是递归完成的：当前状态的值是当前奖励加上后续状态的平均值（在环境P（s | a，s0）的随机转换规则下平均）。 最优策略优化了这些功能，这也可以通过修改策略以实现价值功能最大化而依次实现。 但是，这假定了转换规则P（s | a，s’）的知识。 在该理论的进一步发展中，表明跟踪动作值函数Qπ（s，a）由

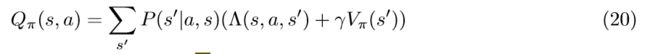
不仅将值分配给状态，还可以将后续操作修改为在线学习算法。 特别是，可以通过对操作值的当前奖励（在时间步t处）进行加权平均，然后对后续操作值的最高可能Q值进行加权平均，来连续估计Q值：

请注意，访问最佳Q值可以成功地找到最佳策略：给定状态，只需选择一个具有最高Q值的动作，但是上面的算法并没有说明代理在学习时应该采用哪种策略。 在（Watkins和Dayan，1992）中，证明了该算法是由等式的更新规则指定的。 称为Q学习，实际上会收敛到最佳Q值，只要代理对给定任何状态的所有操作都采用非零概率的固定策略（参数αt是时间的函数，必须满足某些条件） ，并且γ应该是目标指标Rγ的γ。

  从本质上讲，此结果成功地解决了RL的第一个问题，即最佳策略由代理在极限范围内“学习”，但原则上从未实际使用。 对于所有学习代理，都使用 极限贪婪无限探索（GLIE）策略证明了Q学习更新收敛到最佳Q值，从而达到了最佳行为。 顾名思义，这样的策略在渐近极限下以估计的最高值执行动作。

  同时，无限探索意味着，在极限条件下，将无限次尝试所有状态/动作组合，以确保找到真正的最佳动作值，并避免局部最小值。 通常，这两个竞争属性之间的最佳交易，学习空间的探索和所获得知识的利用对于RL是最典型的。 还有许多其他基于状态值或动作值优化的RL算法，例如SARSA，各种值迭代方法，时间差异方法等（Sutton和Barto，1998）。 在最近的时间里，通过使用状态-作用-值函数的参数化近似值（函数近似值和强化学习之间的杂种）已取得了进展，这减少了可用Q函数的搜索空间。在这里，将深度学习与价值函数逼近与RL相结合的结果特别成功（Mnih等，2015），同样的方法也为AlphaGo（Silver等，2016）系统奠定了基础。 这使我们进入了不同的方法类别，这些方法 不优化状态或动作值函数，而是通过执行梯度下降估计或策略空间中其他直接优化的方法来学习完整的策略。 只要通过较少数量的参数间接指定策略，这是可行的，并且在某些情况下可以更快（Peshkin，2001）。

  到目前为止，我们讨论的方法考虑了环境的特殊情况，其中环境是马尔可夫式的，或者与此有关的环境是完全可观察的。 最常见的概括是所谓的 部分可观察的MDP（POMDP） ，其中基础MDP结构被扩展为包括一组观测值O和一个由条件概率分布PPOMD P（o∈O | s∈S定义）的随机函数， a∈A）。 代理不再可以直接访问环境状态集，而是 代理从集合O中感知观察结果，该结果间接且通常随机地取决于分布P，由POMDP给出的实际不可观察到的环境状态 ，以及代理商最后采取的行动。 POMDP具有足够的表现力，可以解决许多现实世界中的问题，因此 是AI中的通用世界模型，但与MDP相比，它要难得多。

如前所述，POMDP的设置使我们更接近于任意环境设置，这是（通用）人工智能领域的模型。

  AGI的上下文通常与现代的机器人技术密切相关，在这种观点中，可以观察到的内容以及可能采取的行动的结构不仅取决于环境的性质，还取决于主体的（身体）约束： 机器人配备有传感器，用于指定和限制机器人可以观察或感知的内容以及执行器，以限制可能的动作。 在这种以代理人为中心的观点中，我们通常谈论一组感知器（代理人可以感知的信号），它可能对应于完整状态或部分观察，具体取决于代理人环境的设置。

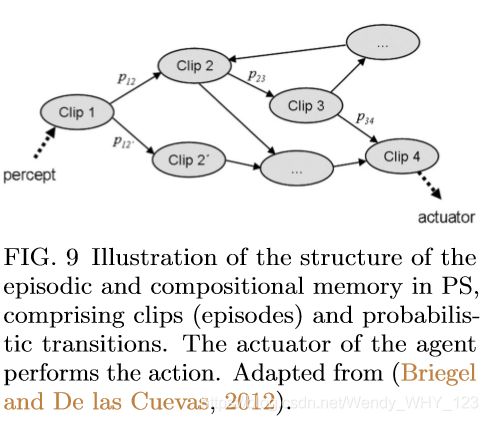
  后一种观点认为，感知/行为结构来自主体的物理构成和环境，我们将其称为具体化的观点，这是针对 射影模拟（PS） 模型开发的起点之一。 PS是用于AI的受物理学启发的模型，可用于解决RL任务。 该模型的核心是所谓的 情节记忆和成分记忆（ECM），它是片段的随机网络，请参见图9。

  剪辑是自传短片（即特征的记忆）的表示。 使用允许基本的创造力概念的记忆构成方面，代理还可以结合实际记忆来生成虚拟的，实际上并不需要发生的，可想象的剪辑。 更正式地说，片段可以递归地定义为记忆的感知或动作，或者片段的其他结构（例如序列）。 给定当前的感知，PS代理会调用其ECM网络在其剪辑空间（其结构取决于代理的历史）上执行 随机游走，然后将自己投射到可以想到的情况中，然后再采取行动。 该模型的各个方面已经进行了有效的量化，并且还用于量子实验和机器人技术，我们将在VII.A节中更加关注此模型。

a. 可学习并学习效率高的RL（Learning efficiency and learnability for RL）

  如本节简介中所述，没有免费午餐定理也适用于RL，并且任何有关学习的陈述都要求我们限制可能的环境空间。例如，“有限空间，与时间无关的MDP”是一个限制，它允许相对于某些标准功绩指标进行完美学习，这是Q学习算法首次证明的。除了 学习性 之外，最近还探索了RL任务的 样本复杂性 概念，从不同角度解决了这个问题。 RL设置的样本复杂度理论比有监督的学习要涉及得多，尽管最基本的需求仍然保持不变：在代理学习之前，需要多少交互步骤。学习自然可以意味着很多事情，但是最通常的意思是代理学习最优策略。与监督学习不同，RL在确定最佳性方面具有额外的时间维度（例如，有限的或无限的视野），从而导致人们可以探索更大的选择空间。关于这一重要研究领域的更多详细信息不在本综述的讨论范围之内，我们将感兴趣的读者推荐给例如Kakade的论文（Kakade，2003年）也很好地回顾了一些早期工作，并发现了许多基本情况下RL的样本复杂度界限。 （Lattimore et al。，2013; Dann and Brunskill，2015）。