使用几何构造用于确定重构相空间的嵌入大小
Determining embedding dimension for phase-space reconstruction using a geometrical construction
- 摘要
- Ⅰ 引言(Introduction)
- Ⅱ 识别假邻居节点的方法(THE METHOD OF FALSE NEIGHBORS)
- Ⅲ 几个例子的数值结果
- A.清除数据和“噪音”
- B 实际数据
- Ⅳ 结论与评论
作者:Matthew B.Kennel,Reggie Brown , Henry D. I.Abarbanel
翻译:Wendy
摘要
我们通过观察在d→d + 1的嵌入维数变化下近邻的行为来研究确定可接受的最小嵌入维数的问题。当通过投影产生的最近邻居数在维度dE中为零时,吸引子已在该维度上展开。dz的精确确定被“噪声”所笼罩,我们研究了噪声改变dE确定的方式。我们的标准还指出了通过选择小于dE的嵌入尺寸而导致的错误。 该研究可能对观察到的时间序列的实际分析有用。
Ⅰ 引言(Introduction)
在分析非线性系统中观察到的时间序列以进行相空间的时延重构以观察动力学方面已是一个非常熟悉的问题。这是通过使用观测到的标量的时间延迟形式:x(t0 + nΔt)= x(n)作为相空间的坐标来实现的。 根据观察结果,使用d维空间中的多元矢量![]()
来跟踪系统的轨道。y的时间演化用 y(n) →y(n +1)表示。实际上,在此重建中时间延迟T和嵌入维数d的问题有很多答案。这里,我们对于这个问题给与一个清晰明确的回答:用作嵌入维数d的值多少比较好? 我们直接通过解决嵌入过程引起的拓扑问题来做到这一点。我们的过程确定与轨道y(n),n =1,2, . . . , N,相关的吸引子上每个点的“假最近邻”(由于嵌入空间太小而看起来最接近的点)的数量。当最近的虚假邻居数降为0时,我们将吸引子展开或嵌入到d维欧式空间中。
观测值x(n)是系统的多元状态空间在x(n)的一维轴上的投影。延时(或任何其他)嵌入的目的是将投影展开回代表原始系统的多元状态空间。 Mane和Takens的一般拓扑嵌入理论指出,当吸引子的尺寸为dA时,选择d>2dA的轨道的所有自交叉点(即吸引子)将被消除。轨道的这些自相交是投影的结果,并且嵌入过程试图消除这种情况。回顾过去,可以通过时间延迟方法将熟悉的Lorenz吸引子dA = 2.06嵌入d = 3中,从而注意到Mane和Takens的结果只是一个充分条件。这与定理相反,该定理仅告诉我们d = 5肯定会完成任务。悬而未决的问题是,给定标量时间序列,最小嵌入维数dE的合适值是多少?从嵌入过程的数学观点来看,使用最小嵌入尺寸dE或任何d≥dE都无关紧要,因为一旦吸引子展开,定理的工作就完成了。对于物理学家来说,故事却大不相同。 在调查一个人希望提出的任何后续问题(李雅普诺夫指数,预测等)时,以任何大于数据要求的最小值的维度进行工作都会导致过多的计算。由于这种“噪声”将填充并支配没有动态作用的嵌入空间的其他d-dE尺寸,因此还会增加由于舍入或仪器误差引起的污染问题。
选择最小嵌入尺寸dE的常用方法是计算吸引子上的一些不变量。通过增加用于计算的嵌入维数,便可以在不变量的值停止变化时注意到这一点。由于 这些不变量是吸引子的几何特性,因此对于d≥dE(即,在几何形状展开之后),它们变得与d无关。这种方法的问题在于,它通常非常耗费数据并且肯定是主观的。 此外,分析没有表明选择一个太低的嵌入尺寸会付出代价。我们已经讨论了选择太大嵌入尺寸的代价。
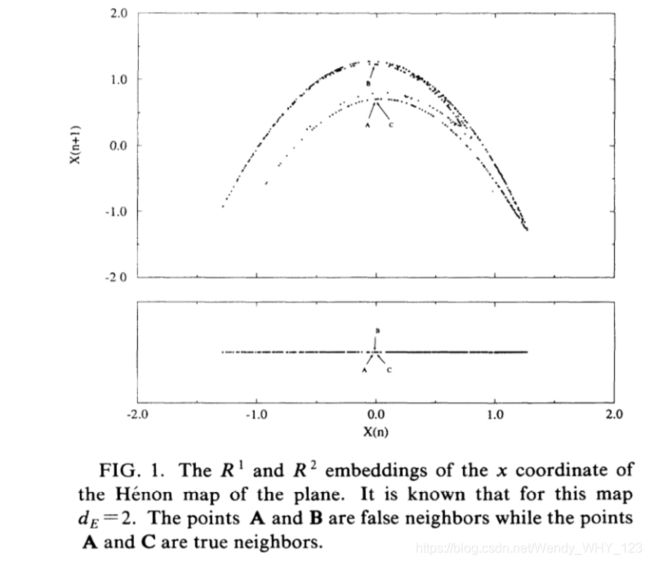
在本文中,我们基于以下想法提出计算:在从维d到维d + 1的传递中,可以区分在轨道y(n)上是“真实”邻居的点和在轨道y(n)上的点是 “假”邻居。虚假邻居是数据集中的一个邻居,仅是因为我们正在太小的嵌入空间(d<dE)中查看轨道(吸引子)。当我们获得足够大的嵌入空间(d>dz)时,多元相空间中每个轨道点的所有邻居都将是真实邻居。在飞机的Henon映射上可以找到这种行为的简单示例。在图1中,我们将Henon图的吸引子显示为在d = 1维相空间(x轴)上以及在d = dE = 2维嵌入空间中的投影。点A和B在x轴上的投影中似乎是相邻的。 但是,它们之所以成为邻居,完全是因为我们在太小的嵌入空间中观察吸引子的轨道。 在d = 2维嵌入空间中查看时,它们不再是邻居。说明点A和B是虚假邻居。 相反,点A和C是真正的邻居。这是因为它们在d = 1维(x轴)上是邻居,在d = dE = 2时以及所有更高的嵌入维数也是邻居。 我们将在第二节中回到并充分发展这一点。
在撰写本文的过程中,我们发现Liebert,Pawelzik和Schuster(LPS)的文章报告了相同的基本概念,但以完全不同的方式实现了该基本概念。我们从这些作者那里发现了截然不同的结果。 我们对他们的观察和结论有几条评论。他们的方法似乎比较耗时,但是只是一个常数。 此外,他们的方法没有产生本想法的理想特征之一。 即,我们提供使用太小的嵌入维数时遇到错误的估计。我们还发现了Bumeliene,Lasiene,Pyragas和Cenys [10](BLPC)的较早论文,其中引用了Pyragas和Cenys [11]的更早论文,该论文具有寻找虚假邻居的基本几何构想,并在之后再次实现另一种时尚。 我们还将对这些论文发表评论。
在嵌入中使用什么时间延迟的问题在逻辑上独立于拓扑问题,即必须有多大的空间才能消除错误的邻居。时滞T的确定需要独立于Mane和Takens的拓扑参数的信息。 这可以理解,因为他们的论点原则上适用于任何时滞T,因此必须独立于有关T的考虑。时滞问题是动态的,而不是几何的。 为了确定T,我们使用Fraser和Swinney的信息理论技术。
Ⅱ 识别假邻居节点的方法(THE METHOD OF FALSE NEIGHBORS)
吸引子的重要特征之一是,它通常是相空间中的紧凑物体。因此,吸引子上的轨道点在该相空间中获取了邻居。 这些邻居的效用尤其是,它们允许将有关相空间邻域如何演化的信息用于生成方程,以预测吸引子上或附近的新点的时间演化。 它们还允许对系统的Lyapunov指数进行精确计算。
在一个嵌入尺寸太小而无法展开吸引子的情况下,由于动力学的原因,并非所有彼此靠近的点都将成为相邻点。实际上,由于吸引子的几何结构已投影到较小的空间中,因此某些对象实际上会彼此远离并只是作为邻居出现(参见第I节)。如果我们在d维上,并且用y’r’(n)表示y(n)的第r个最近邻,则从等式(1),得出点y(n)与该点之间的欧几里得距离的平方邻居是
 在通过时延嵌入从维d变为维d +1时,我们在每个向量y(n)上添加了第(d +1)个坐标。这个新坐标只是x(n + Td)。现在我们问,在(d+1)中,y(n)与在第d维中确定的第r个邻居之间的欧几里得距离是多少?在添加了第(d +1)个新坐标后,y(n)与我们在d维中确定的第r个最近邻居之间的距离为
在通过时延嵌入从维d变为维d +1时,我们在每个向量y(n)上添加了第(d +1)个坐标。这个新坐标只是x(n + Td)。现在我们问,在(d+1)中,y(n)与在第d维中确定的第r个邻居之间的欧几里得距离是多少?在添加了第(d +1)个新坐标后,y(n)与我们在d维中确定的第r个最近邻居之间的距离为
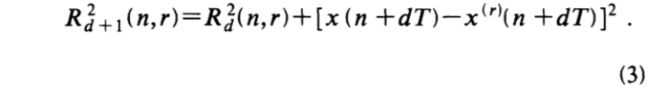
捕获嵌入错误的标准是,从尺寸d到尺寸d +1时,y(n)和y’r’(n)之间的距离增加很大。距离的增加可以很容易地用等式(2)和(3)来表示。 我们通过将任何为其指定的邻居指定为虚假邻居来陈述该标准 其中Rtol是一个阈值。在下面的数值工作中,我们将研究准则对Rtol的敏感性,并且我们会发现,对于Rtol≥10,可以清楚地识别出错误的邻居。仅考虑最近的邻居(r = 1)并询问轨道上的每个点(n = 1、2,…,N)就足以确定X个最近的邻居中有多少是假的就足够了。 我们将计算结果记录为具有错误最近邻的所有轨道点的比例。
其中Rtol是一个阈值。在下面的数值工作中,我们将研究准则对Rtol的敏感性,并且我们会发现,对于Rtol≥10,可以清楚地识别出错误的邻居。仅考虑最近的邻居(r = 1)并询问轨道上的每个点(n = 1、2,…,N)就足以确定X个最近的邻居中有多少是假的就足够了。 我们将计算结果记录为具有错误最近邻的所有轨道点的比例。
在我们报告这些计算之前,我们指出,仅凭此标准不足以确定合适的嵌入尺寸。为了说明这一点,我们注意到,当我们使用该标准检查白色“噪声”(“噪声”是指与计算机化随机数生成器相关的超高维吸引子。)的嵌入尺寸时,该标准错误地报告了该噪声可以嵌入很小的尺寸空间中。问题是,即使y“1’(n)是最接近y(n)的邻居,但不一定接近y(n)。确实,随着我们在嵌入维度上的移动,利用来自噪声信号的有限数据,Rd(n)≡ Rd(n,r = 1)的实际值与吸引子RA的大小相当。因此,最接近y(n)的邻居并不接近y(n)。这种行为源自以下事实:尝试用固定数量的点均匀地填充d维中的对象,这意味着这些点必须进一步移动,并且 随着d的增加而进一步分开。我们注意到,随着我们增加噪声信号中数据点的数量,嵌入维度(虚假邻居的数量下降到几乎为零的维度)系统地增加了。在无限数量的数据的限制下,我们会发现嵌入维数d也发散到无穷大。这与许多动力学系统常见的低维吸引子相反。 对于低维动力系统,增加吸引子上数据点的数量不会改变dE。
但是,在实际设置中,数据点的数量通常不会非常大。我们已执行以下准则来处理数据集大小受限的问题:如果距离y(n)的最近邻居不是紧密的[Rd(n)≈ R z]并且它是错误的邻居,则距离Rd +1(n) 通过将第(d + 1)个分量与数据矢量相加而得到的为Rd +1(n)= 2RA。就是说,如果它们是假的最近邻居,则即使彼此遥远但最近的邻居也将在吸引子的末端彼此伸展时被拉伸到末端。
我们将第二个标准写为 在我们的工作中,我们主张通过结合使用这两个标准,如果任何一个测试失败,则将最近的邻居(如维d所示)声明为假的。
在我们的工作中,我们主张通过结合使用这两个标准,如果任何一个测试失败,则将最近的邻居(如维d所示)声明为假的。
我们用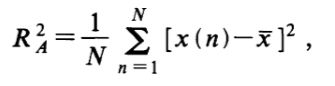 计算RA,其中
计算RA,其中 RA的其他选择(例如,关于x的绝对偏差)不会改变我们的结果。 读者可以选择吸引子大小的其他任何估计值。
RA的其他选择(例如,关于x的绝对偏差)不会改变我们的结果。 读者可以选择吸引子大小的其他任何估计值。
在图2中,我们显示了单独应用第一个标准,单独应用第二个标准,然后在来自Lorenz三维模型的数据集中联合应用的结果。
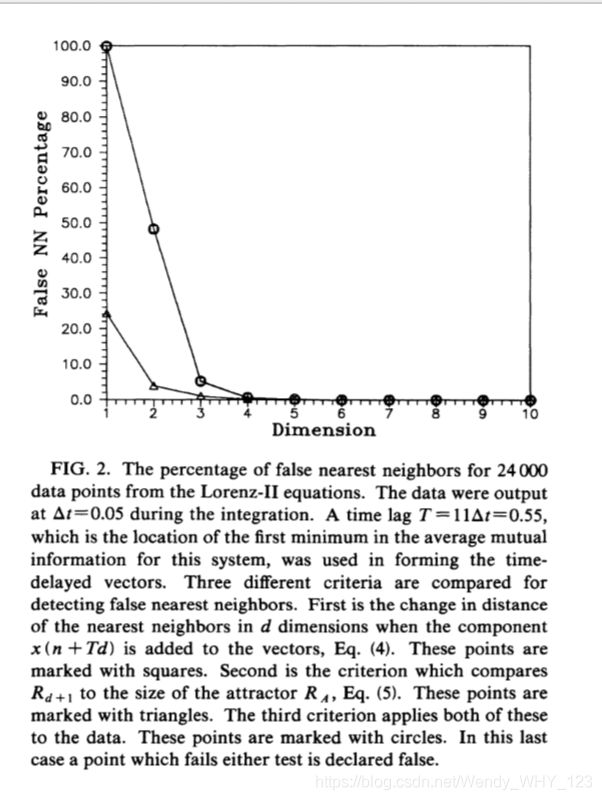
 我们使用值a = 0.25,b = 4.0,F = 8.0和G = 1.0,其中Lorenz指出遇到不规则行为。吸引子的尺寸dz略大于2.5。 我们使用可变阶Adams积分器生成了该图中使用的数据,输出为Δt = 0.05。平均互信息的第一最小值出现在T = 0.85 = 17Δt 。 这是时间延迟T, 我们从x(n)= x(t0 + nΔt)的样本中重建相空间矢量y(n),在图2中总共使用了25000个数据点。显然,联合标准[(4)和(5)]以及每个单独的标准[(4)或(5)]对于该吸引子产生了dE = 6的嵌入尺寸。 在这种情况下,结果实际上与Mane和Takens的d>2dA界相同。 对于此计算,我们使用值Rtol= 15.0和Atol= 2.0。 我们将在第三节中说明该方法对数据点N的数量和Rtol的值的依赖性。
我们使用值a = 0.25,b = 4.0,F = 8.0和G = 1.0,其中Lorenz指出遇到不规则行为。吸引子的尺寸dz略大于2.5。 我们使用可变阶Adams积分器生成了该图中使用的数据,输出为Δt = 0.05。平均互信息的第一最小值出现在T = 0.85 = 17Δt 。 这是时间延迟T, 我们从x(n)= x(t0 + nΔt)的样本中重建相空间矢量y(n),在图2中总共使用了25000个数据点。显然,联合标准[(4)和(5)]以及每个单独的标准[(4)或(5)]对于该吸引子产生了dE = 6的嵌入尺寸。 在这种情况下,结果实际上与Mane和Takens的d>2dA界相同。 对于此计算,我们使用值Rtol= 15.0和Atol= 2.0。 我们将在第三节中说明该方法对数据点N的数量和Rtol的值的依赖性。
对于有噪声的数据,结果是完全不同的。在图3中,我们显示了在x和(n)之间均匀分布的噪声在-1和1之间的假最近邻准则的相似比较。我们使用时间延迟T = 1,并且再次使用N = 25000。在这里,我们看到第一个条件,等式(4)未能表明需要较高的嵌入尺寸。 然而,第二个标准,等(5)却可以产生预期的答案。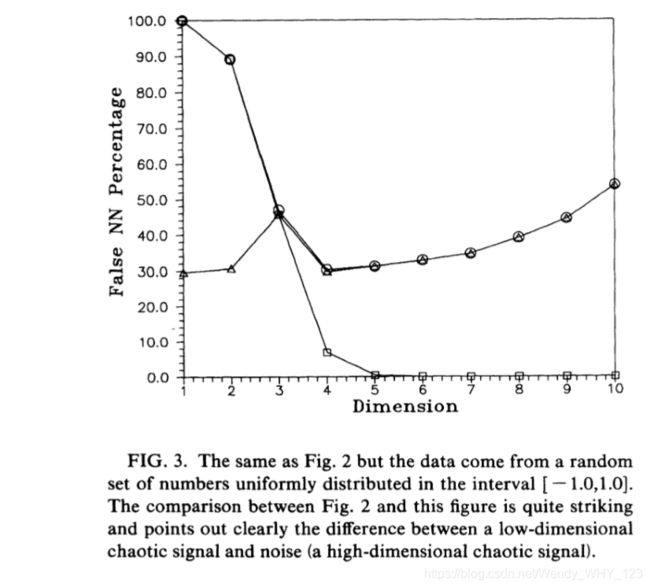 当然,联合标准也适用,并且正如人们所期望的那样,随着d的增加跟踪第二个标准。 在我们尝试的所有示例中都可以看到 低维混沌和高维混沌之间的显着差异。 此后,我们仅引用共同应用我们的标准的结果:未通过任何一项测试的最近邻居被判别为假。
当然,联合标准也适用,并且正如人们所期望的那样,随着d的增加跟踪第二个标准。 在我们尝试的所有示例中都可以看到 低维混沌和高维混沌之间的显着差异。 此后,我们仅引用共同应用我们的标准的结果:未通过任何一项测试的最近邻居被判别为假。
重要的是要注意,由于报告了错误邻居的百分比,所以在每种情况下我们都能够确定嵌入的维数。例如,在上述的Lorenz 84吸引子的情况下,如果我们选择使用d = 5而不是d = 6的嵌入维,则将剩余0.18 %的虚假邻居。对于许多目的来说,这可能是一个可以接受的小数目。 物理学家很可能会选择接受该错误,以使对来自该系统的数据执行的任何进一步计算更加有效。实际上,仅选择d = 4的错误就不是实质性的,因为错误邻居的百分比仅为0.59%。 甚至可以将这些邻域解释为非常大的局部Lyapunov指数的孤立实例。即使嵌入正确,很高的不稳定性增长率也可能导致Rd +1/ Rd非常大。在其他研究中,我们发现对于短时间间隔,有限时间李雅普诺夫指数的分布可能非常广泛。当前情况的含义是,可能存在一些邻域,其最大的局部Lyapunov指数位于分布的极值范围内,由于内在的动力学原因,假邻居准则(以及任何其他类似类型的度量)将失败。 仔细地将虚假的邻居与较高的局部指数区分开来仍然是一个尚未解决的问题,但是这个问题似乎并不十分严重。
Ⅲ 几个例子的数值结果
A.清除数据和“噪音”
我们已经在各种简单模型上实现了刚刚描述的方法。 让我们从前面讨论的Lorenz-II模型开始。 使用相同的时间延迟T = 17Δt,我们检查了我们的方法对容差Rtol的依赖以及数据集N的长度。图4显示了d = 1中虚假邻居百分比与这两个变量的关系。显然,除了少量的数据N = 100和较大的Rtol值外,虚假邻居的方法也不会将d = 1表示为良好的嵌入维数。
对于d = 5,图5显示了相同的依存关系,即最近邻百分比与Rn和N的关系。 显然,当数据点的数量N足以填充d = 5维的吸引子,并且公差等级为Rtol≥15时,我们可以放心地选择d = 5作为嵌入维。如上所述,最好也可以选择d = 6,虚假最近邻居的百分比恰好降为零。 但是,与d = 5相关的误差非常小(约0.18%),因此最好使用d = 5。此外,我们还检查了该系统的d = 1,2,… ,10的结果。
这里的信息很清楚。 对于固定数量的数据,人们始终无法探索吸引子的最佳细节,因此一些非常近的邻居可能仍会显示错误。 有了大量数据,这种外观就被消除了,并且暴露了邻居的分析。 在对来自未知来源的数据集进行分析时,需要做出一些判断。 我们认为,无论哪个维度产生的假最近邻的百分比低于1%,都应该作为有效的嵌入维度很好地工作,这没有什么害处。
回到均匀噪声,我们在图6-8中显示了d = 1,d = 4和d = 8时假近邻百分比对N和Rtol的依赖性。 在每种情况下,该百分比均处于平稳状态,并且从不表示低维度尺寸将被视为良好的嵌入。 即使N和Rtol都增长,错误的最近邻百分比仍保持约25%。
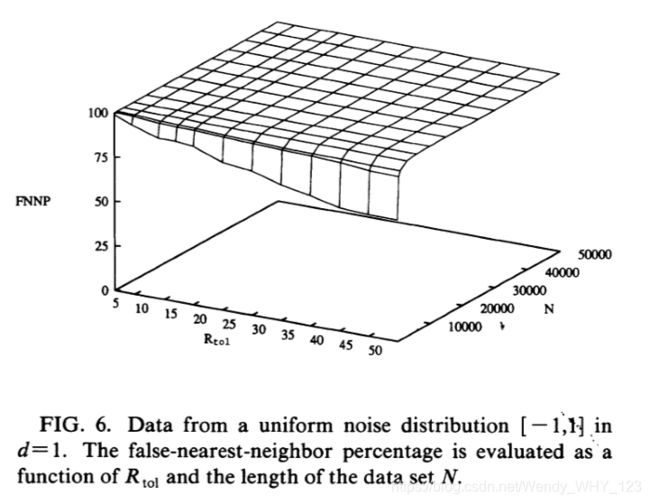
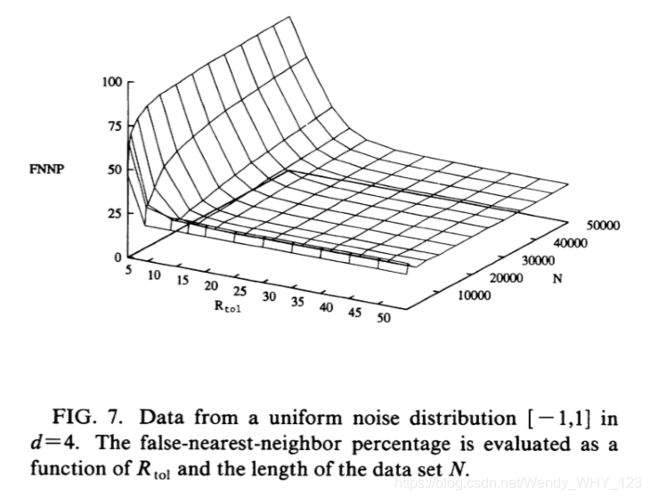
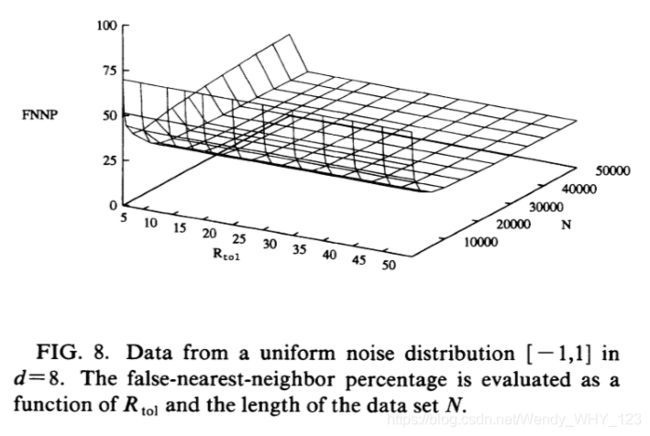
图9-12,我们将飞机的Ikeda映射显示为其自身的结果。
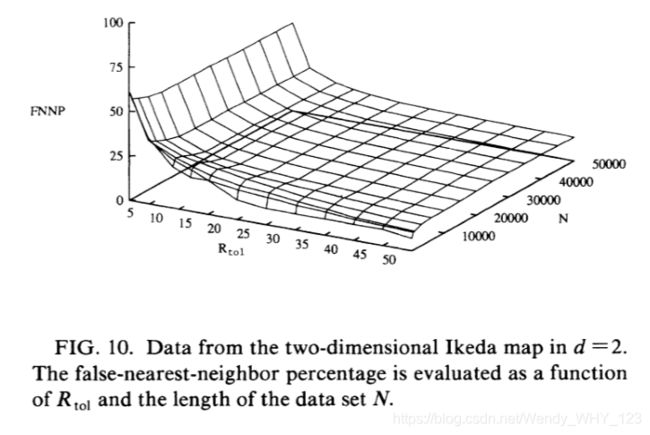
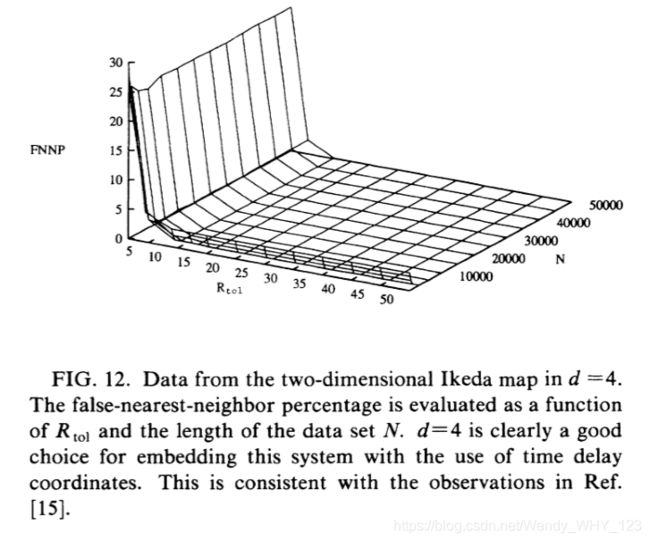
其中p=1.0,B=0.9,K=0.4,α=6.0,z(n)是复杂的。吸引子的维数与其对应的映射相关,大约是dA=1.8。从其它方面考虑,已知需要d = 4的嵌入尺寸以通过时延嵌入使吸引子折叠。该性质在图中清楚地示出,其中示出了d = 1、2、3和4的结果。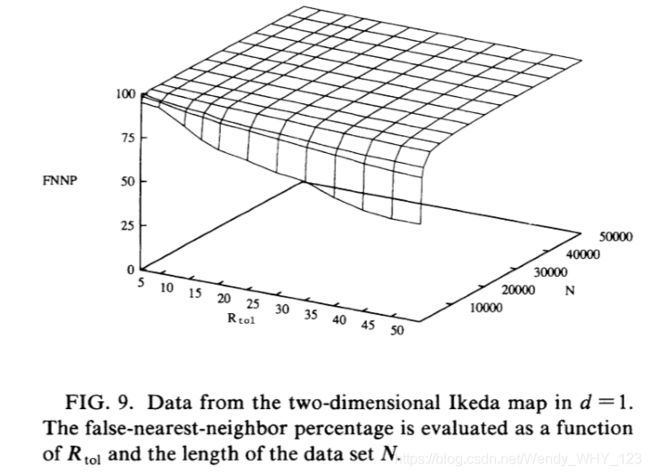

我们还将我们的方法应用在了确定性的低维度嵌入的系统,如Lorenz-Ⅰ,Henon映射,Rossler吸引子。Mackey-Glass延时差分方程。结果与上面显示的一样惊人,并且在后两种情况下与LPS所发现的最小嵌入尺寸是一致的。 因为要点很明确,所以我们避免将读者淹没在数据中。 但是,也许我们应该添加一点,那就是在遍历数据集并确定哪些点与点y(n)的邻近点时,我们使用“ k-d”树的排序方法来减少计算时间 O(n²)到O(Nlog10 [N])。因此,在SUN Sparcstation 2工作站上,所需的每次计算都需要几分钟。
B 实际数据
上面的示例绝不会以原始,无噪声的方式将数据传递给用户。 从实际实验设备获得的时间序列始终包含信号和噪声。 对于“纯噪声”显示的结果肯定表示信噪比从正无穷大开始减小。 我们已经研究了噪声降低我们为一组示例系统获得的结果的方式。 我们期望并看到的基本趋势是,随着信噪比降低,有效的嵌入尺寸增加。
图13我们展示了我们的联合标准方法在Lorenz-Ⅰ系统上N=25000个吸引子的结果。Lorenz-Ⅰ的方程如下: 使用参数值σ=16,b=4,r=45.92。数据由可变阶Adams代码生成,输出为 Δt =0.02。对于该系统,平均互信息的第一最小值为T≈0.1=5Δt。我们使用的公差值为Rtol=15.0 和 Atol=2.0。轨道已被均匀分布在[-L,L]的噪声所污染,其中L / RA = 0,0,0.005、0.01、0.05、0.1和0.5。最后一个噪声电平对应于功率约6 dB的信噪比[20log10(RA/ L)]; 即,非常低的信噪比。在存在噪声的情况下,此吸引子的嵌入尺寸的增加确实非常缓慢,并且只有在最后一个污染严重的情况下,它才失败。 (当信噪比降至0 dB时,错误最近邻准则将失效,并且我们发现在该级别受污染的Lorenz-I信号与噪声是无法区分的。)在L/RA= 10%且d = 3的情况下,我们有7.8%的虚假最近邻居。 对于d = 4,此数字下降到2.5%,并且对于更高的嵌入尺寸,稳定值会下降。
使用参数值σ=16,b=4,r=45.92。数据由可变阶Adams代码生成,输出为 Δt =0.02。对于该系统,平均互信息的第一最小值为T≈0.1=5Δt。我们使用的公差值为Rtol=15.0 和 Atol=2.0。轨道已被均匀分布在[-L,L]的噪声所污染,其中L / RA = 0,0,0.005、0.01、0.05、0.1和0.5。最后一个噪声电平对应于功率约6 dB的信噪比[20log10(RA/ L)]; 即,非常低的信噪比。在存在噪声的情况下,此吸引子的嵌入尺寸的增加确实非常缓慢,并且只有在最后一个污染严重的情况下,它才失败。 (当信噪比降至0 dB时,错误最近邻准则将失效,并且我们发现在该级别受污染的Lorenz-I信号与噪声是无法区分的。)在L/RA= 10%且d = 3的情况下,我们有7.8%的虚假最近邻居。 对于d = 4,此数字下降到2.5%,并且对于更高的嵌入尺寸,稳定值会下降。
图13说明了我们嵌入维度的方法。 再说一遍,实际的问题是应该使用哪种嵌入维度来捕获观察到的数据的特征。 我们肯定会选择d = 4作为有效的嵌入尺寸,并将2.5%的平稳段解释为噪声效应。确实,使用数据执行的第一个任务之一就是应用最近提出的几种降噪或分离方法之一[24-28]。我们提出的方法将通过选择执行降噪的展开尺寸来提供准确的起点。在从污染中分离出信号之后,可以轻松地返回到伪近邻方法来确定另一种(可能更小的)嵌入尺寸,以用于分析信号。实际上,由于这两种方法都需要了解动力学或观察动力学的干净轨迹,因此仅在不需要“干净”系统的情况下,言论可能会起作用。在仅观察到干净轨迹的概率方法中,当前的假最近邻技术将提供关于嵌入尺寸的直接,有用的答案,在该尺寸中可以清洁后续的噪声数据。
Ⅳ 结论与评论
我们通过评论本文与LPS 和BLPC 的关系开始本节。应该提到的是,所有这些方法背后的一般思想已经存在了一段时间,例如,参见参考文献3中的图3,实际上只是对线性控制系统状态空间公式中所涉及问题的非线性动力学领域的概括。
LPS论文和本论文都提供了相同基本思想的实现。 我们每个人都使用时间延迟坐标,并将虚假邻居的消失归因于该数据的最小嵌入维数。从这一点出发,我们的方法是不同的。 LPS技术使用小的邻居,而我们使用单个邻居。 然后,他们计算两个距离Dd +1(n,r,d)和Dd +1(n,r,d + 1)。Dd +1(n,r,d)是y(n)与其第r个邻居之间的距离。对于这种情况,以d维执行确定哪个是近邻的计算,而以(d + 1)维执行邻居之间距离的计算。Dd +1(n; r,d + 1)也是y(n)与第r个邻居之间的距离。然而,对于这种情况,确定哪个是近邻的计算和到该近邻的距离的计算都以(d + 1)维执行。比率Dd +1(n; r,d)/ Dd +1(n; r,d + 1)≡Q1定义它们的数量Q1。
LSP继续根据Dd (n; r,d)/ Dd (n; r,d + 1)≡Q2,来定义Q2。在这种情况下,邻居之间的距离的计算以d维为单位。分子的d维数和分母的(d + 1)维数用于标识第r个最近邻居。 然后,LPS在一个邻域中检查乘积Q1Q2的几何平均值(在他们所报告的情况下,前十个最近邻域)。 我们的第一个标准等式(4)可以看成是它们的一部分Q1与它们的一部分Q2之比。 LPS的统计量称为W,是各个几何平均值附近的算术平均值的对数。
为了找到最小的嵌入尺寸,我们的方法和LPS的方法使用相同的基本原理。 但是,在我们的案例中,统计和解释更为简单。错误邻居的比例在绝对范围内,始终在0到1之间,而对于LPS,除非收敛非常尖锐,否则尚不能立即清楚地知道什么构成了足够小的统计量。 如果有人看到一个0.1%的虚假邻居的稳定区,并且嵌入尺寸增加了,而可能只有10%的稳定区,那么您可能会很有信心,已经完成了对干净混沌吸引子的良好重构。 LPS并未检查噪声对其算法的影响,但在简短的比较中,我们发现在纯均匀噪声下,其统计随着嵌入尺寸的增大而继续降低,而我们的水平则处于较高水平。这并不奇怪,因为他们的统计信息使用的信息与我们的信息相同,但是没有我们认为必须防止纯噪声的其他标准。 对于添加到Lorenz-II吸引子的中等噪声水平(10%),LPS统计量没有如假邻居准则那样随着嵌入尺寸的增加而具有确定的平台,因此我们发现在最小嵌入尺寸的识别中更容易出现后一种情况。
LPS还使用其统计信息选择嵌入的时滞。他们定义了一个新的数量W = W / T并根据T寻找W的最小值。我们承认没有完全理解除以T背后的动机。单独的W数量提供了我们直觉上期望的一般行为,并且还使用虚假邻居统计进行观察。对于大的T,由于状态空间向量的元素正Lyapunov指数而变得更加去相关,因为吸引子看起来更像噪声,所以虚假邻居的比例以及W统计量都会增加。对于足够小的时间滞后,吸引子最终会塌陷到一维对象上,因此估计的嵌入维将虚假地降低。 如果一个人随后忽略了由除法在大T处创建的W中的新最小值,那么用T除法似乎是缓解后一个问题的一种方式。
与嵌入维的情况相反,这些定理没有定义要使用的“正确”时间延迟,而是必须选择一种条件,该条件给出在给定采样率下有限数量的数据和LPS准则下仅给出合理结果的条件。 我们的方法,特别是针对由于嵌入不当而产生的严重错误,在实践中似乎比LPS的方法对时间延迟不敏感。 根据个人的观点,这一事实可能是好的,也可能是不好的。
我们在池田地图上的示例还表明,如LPS所建议的那样,嵌入维数的选择对消除虚假Lyapunov指数的问题几乎没有作用。在时间延迟嵌入的尺寸大于“真实”动力学的尺寸的情况下,仍然必须通过动力学方法识别描述系统的李雅普诺夫指数,而不是通过欧几里德坐标来确定时间延迟嵌入的伪像。
BLPC论文比LPS论文更贴近我们的思想。BLPC标识一个数量σd(e),它是所有对点(用n和m标记)中y(n)和y(m)的[x(n + dT)-x(m + dT)]²值的吸引子的平均值。 ),彼此之间的距离e内的所有分量都除以轨道上此类点的数量。这实际上是在数据点y(n)的半径e&d范围内所有邻居的Rd+1² +(n,r)-Rd(n,r)的吸引子上的平均值。然后,它们显示各种尺寸d的σd(e),并选择邻域大小e和噪声水平的各种选择,并将其添加到系统的演化方程中。 当此数量与尺寸的曲线出现急剧变化时,他们认为应选择该尺寸作为嵌入尺寸。对于超出此中断的尺寸,σd(e)的值应为e²。 他们还指出,最小嵌入尺寸dE与吸引子d的分形尺寸有关,即dE= 1 + [(dA)的整数部分]。
一般而言,这与我们所做的非常接近。 当然,BLPC必须选择一个邻域大小,据我们从他们的工作中可以看出,他们没有系统地调查此大小对其结果的影响。他们还始终使用4096个数据点,我们怀疑这对于他们调查的数据可能足够了。我们必须为假性最近邻居的标准中选择的容差水平选择一个值,但是我们已经证明了此选择在很大范围的值中的独立性。通过选择邻居大小,显然以与吸引子的大小无关的方式,BLPC实际上确定了当邻居在吸引子周围移动时将包括多少个邻居。由于邻近区域的大小是固定的,并且吸引子上的密度是不均匀的,因此这个数字将随着吸引子的移动而变化。从BLPC的数据中可以看到,σd(e)的值不会下降到高于dE的e,因为它们以某种方式对半径为ev的球内的真实邻居的点进行了多次计数。这确实不是很严重,但是当数据中存在噪声时,可能会以此来欺骗对何时达到dE的估计。 我们还评论说,我们在此处呈现的池田图的示例表明,它们在dE和dA之间的建议连接通常是不正确的。选择邻域大小并询问点何时停止移出那些邻域,这是BLPC算法的本质,与仅使用最近邻域的过程相比,这需要额外的工作和计算成本。这是因为点很可能会出现在许多邻域中,尤其是在邻域大小不小的情况下,就像在多个BLPC示例中一样。
最后,实现虚假邻居思想所需的计算简单性,以及能够(定量和直接)估计嵌入尺寸的各种选择所隐含的误差的能力,应使我们的程序可用于多种设置中。 实际上,我们已经成功地将该方法应用于来自多个来源的实验数据,并且即使在存在噪声污染的情况下,我们也能够毫不费力地,非常有效地确定最小嵌入尺寸。