图同构（graph isomorphism）算法（1）

挖坑。
顺便吐槽，latex换行不能，图片巨大化，缺少自动保存，不小心点了个后退白写半个钟头，这是我熟悉的csdn？？

---

简介

对于同一个图，我们可以用各种不同的形式来描述，这些形式都具有相同数目的边，具有相同数目的顶点，它们有着一一对应的关系，对应的顶点具有相同的连接性。这些图的不同形式，我们称之为图同构。

直观来说，如果图 G1,G2 顶点和边数量相同，且边（具有方向性，即有向图）的连接性相同，这两个图定义为同构。可以认为，G₁的点是由G₂中的点映射得到。

随着上世纪八九十年代一大批（应用）数学家投入到对图论中这个问题的研究，各种研究成果也层出不穷。重要的是应用能很快投入实际。从图像处理识别到视频动态分析，从生物高分子学到文档语言处理，图论中的这个问题也成为相对热门的研究对象。

图同构问题一般可以分为四个不同的研究种类：精确图完全同构、精确子图同构、不精确图完全同构、不精确子图同构。证明已后面三者是NP-Complete问题，第一类问题还没有定论，一般认为是NP问题。这个blog的系列主要研究精确图同构问题。

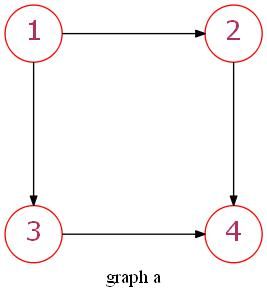
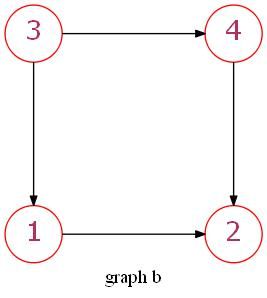
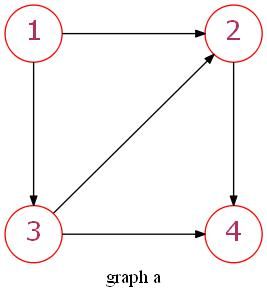
以图a和图b为例：

不言而喻，从图b到图a存在着一组映射：

a1−>b3a2−>b4a3−>b1a4−>b2

因此两图是同构的。这就是exact matching。

子图同构问题，顾名思义描述的是图b能否与图有向a的某个子图同构。还是以上述两个图为例，在图a中增加一条3到2的有向边。此时图a的子图（subgraph）a’和图b同构（显然）。

算法框架

1971年的ACM杂志上，刊登了一篇被人广泛引用的论文。埃因霍温大学的C Bron，对无向图的Maximal Clique问题做了一点微小的工作，然后地位就不知道高到哪里去了。过了40年，某学者在IEEE上发图同构综述，还把这篇论文尊为鼻祖。也许有人要问了，我们前面看的不是有向图吗，为什么要放一篇八竿子打不着关系的文章上来，发ranka是不是也要凑字数凑引文啊？

说毫无关系也是不对的。看下这篇Finding All Cliques of an Undirected Graph，70年代的行文风格简单粗暴，上来也没有像今天写论文或是本文这样缠缠绵绵的引用和简介，intro只有一句话：不在任意一个完全子图里面的完全子图（又称为团，Clique），称之为Maximal Clique（最大团）。然后立刻放出求最大团的两个算法，就像啪啪两枪直刺心脏，毫无一句废话。技巧有二：第一叫做backtracing（回溯），第二叫做branch & bound（剪枝）。虽然目标不同，但这就是解决图同构问题的基本框架（之一）了。两个技巧被后世的高中生们学了去，在OI界大杀特杀，这又是后话。

第一个算法也是无比brute，维持一个搜索状态，不断将点加入到有可能的点集中，直到无法继续扩展。（2b continued…）

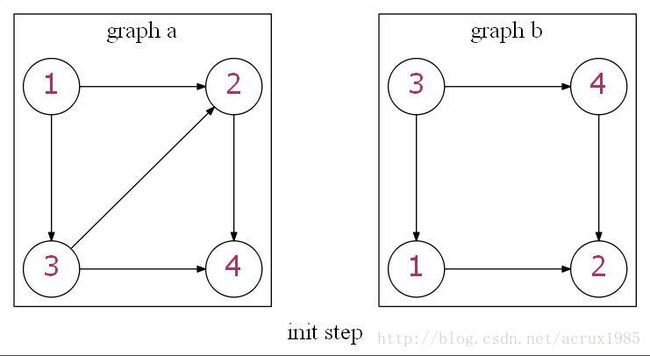
在搜索的基础上，我们可以写一个简单的处理同构问题的框架。以刚才的例子来说，图同构最后得到的结果是一串序列： 3,4,1,2 ，代表b图对a图的映射关系。因此可以进行如下的搜索过程：

上图为初始状态，搜索节点为空，用 {} 表示，先假定a图的搜索顺序为 {1,2,3,4} ，最后形成的搜索结果应为 {(1,bs1),(2,bs2),(3,bs3),(4,bs4)} ，其中 sn 代表b图点搜索的顺序。

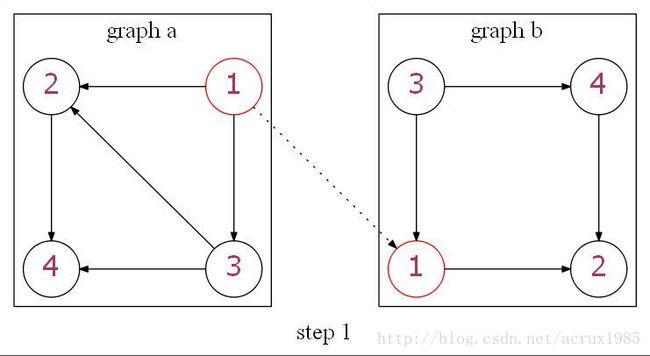
第一步，将b图中的节点1加入搜索，与a图中的节点1对应。映射关系用红色表示。状态为 {(1,1)}

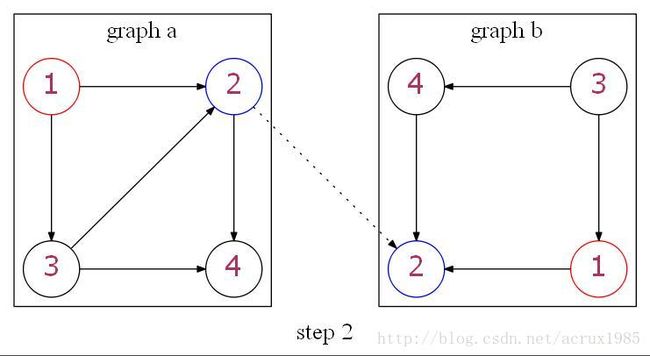
第二步，加入b图中的节点2。因为两个图中1到2都存在一条有向边，所以目前这个状态没有问题。状态为 {(1,1),(2,2)}

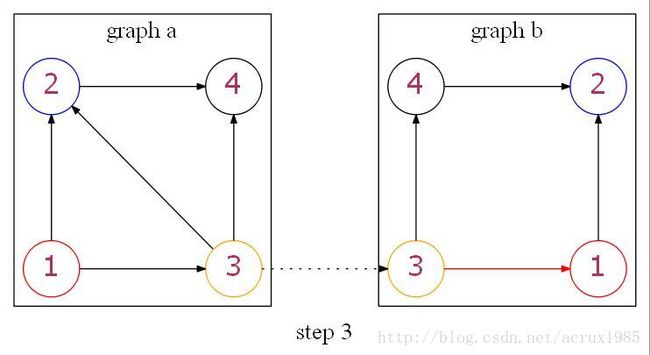
第三步，加入b图中的节点3。检查边的情况，发现图b中红色的边与图a中相对应的边连通性不同，即图a应有一条边从3指向1而实际情况不同。因此搜索回溯，回到第二步中的状态 {(1,1),(2,2)} ，再继续往下加入节点4形成新的状态 {(1,1),(2,2),(3,4)} 。这里检查的准则是，只要当前搜索到的b子图中存在某条边，对应的a子图中就应该存在相对应的边，这样就能够得到b和a中的某个子图同构。

有搜索基础就知道，这其实就一个深度优先搜索（DFS）。以此类推，最后得到完全匹配的状态 {(1,3),(2,4),(3,1),(4,2)}

这是一个比较简单的搜索，但是效率显然低下。问题出在没有利用图a的任何一条性质，而是简单的从1,2…..一直到n搜索a，造成搜索树的大量分叉。那就改改吧！图a本身可以用dfs生成一个图的搜索前序。这样的好处是可以尽快将不可能的情况进行剪枝。直观的来说，a的子图里面边越多，限定的条件也就越多，剪枝的效率越高。所以a的搜索顺序应遵循两个原则：1、出入度多的在前面。2、按照前序。

以下，用生成的数据做了一组简略的测试。图a有15个节点，30条边，图b有15个节点，39条边，测试在图b中找到图a的同构子图。以下图没有双向边，没有点指向本身的圈。对于每个图，数据格式第一行为n m，代表图的节点数量和边数量。下面m行u v 代表从u到v存在有向边。

15 30
1 3
1 4
1 5
1 14
2 12
3 9
3 10
3 11
4 2
4 3
4 10
4 11
5 2
5 10
6 7
6 10
7 11
8 4
8 14
9 4
9 11
9 15
10 2
10 7
12 1
12 11
13 1
13 8
14 9
14 11

15 39
11 5
11 10
11 3
11 13
4 8
5 1
5 9
5 6
10 4
10 5
10 9
10 6
3 4
3 9
7 14
7 9
14 6
15 10
15 13
1 10
1 6
1 2
9 4
9 14
8 11
8 6
12 11
12 15
13 1
13 6
4 1
9 6
2 3
4 12
11 4
7 12
5 7
8 2
4 15

最后用VS2012测试得到结果如下：
算法1遍历1477个状态，算法2遍历171个状态。符合预期。

而在下面这个例子中，两个算法的效率差异是惊人的：

20 50
1 14
2 18
3 10
4 3
4 9
4 11
4 18
5 2
5 12
5 15
6 7
6 8
6 13
7 8
7 15
8 1
9 1
9 12
9 15
11 1
11 2
11 5
11 8
11 14
11 15
11 20
12 6
12 19
13 2
13 16
13 18
14 7
14 12
15 18
16 1
16 3
16 12
16 14
16 19
17 2
17 9
17 10
18 3
18 5
18 6
18 8
18 9
19 8
20 9
20 10

20 64
11 15
18 4
16 13
17 16
17 2
17 6
17 4
10 18
10 1
10 7
12 3
12 5
12 20
3 5
3 7
5 11
2 11
2 1
2 7
6 11
6 18
6 10
6 5
6 15
6 7
6 8
1 12
1 19
20 18
20 14
20 4
15 3
15 1
7 4
14 11
14 16
14 1
14 15
14 19
9 18
9 2
9 13
4 16
4 10
4 12
4 5
4 2
19 5
8 2
8 13
5 13
17 14
14 6
14 7
6 13
2 15
3 8
16 15
12 8
20 2
13 3
20 6
7 1
1 20

针对50条边的图a，算法1搜索了2834001个状态，而改良后的搜索只遍历了953个状态！在稀疏图面前，这个剪枝还是相当强的。（待续）