Stanford Machine Learning 公开课笔记(2) Logistic Regression

最近在Coursera上学习Stanford的Andrew Ng的Machine Learning公开课，也做笔记，写作业。本章是Logistic Regression。记录一下我的笔记。大部分是课堂视频截图，形式比较丑。

写完编程作业(主要用octave来实现，和matlab语法很像)之后，发现写作业并且在系统中提交通过才能给你带来真正地学会了的感觉，推荐认真听课并且独立完成作业。

首先记录自己的几个疑问

1 为什么预测点击率使用的是逻辑回归模型? 

2 当有多个输入变量可能对输出结果造成影响时，如何判断谁的相关性最大？ 

3 输入变量和输出结果是因果关系还是相关关系，这个该如何判断?

4 多个输入变量之间有因果关系和没有因果关系时，对输出结果的影响有什么区别? 

5 octave内自带的fimunc()是如何进行优化的？使用了梯度下降进行优化吗？

学完这节课之后，就可以解决其中的大部分疑问了。

Logistic RegressionWhy Logistic Regression? Why not Linear Regression?
0) focus on the problem of classification
     Logistic Regression是专注解决分类问题的。有些问题虽然看似可用线性回归去，但线性回归的表现没有逻辑回归好。下面会一一阐明此点。
1) classification can be divided into binary classification and multi classification

对比逻辑回归和线性回归在解决分类问题时的差异1

如上图，8个红叉点代表8个sample，根据Tumor Size的不同，Malignant取值也有不同(0或者1这两类)。如果按照使用线性回归模型，可以对这8个sample拟合出一条直线，如上红色的直线，并可以得到上图下方的结论。即Y轴(IsMalignant)在0.5取值是一个阈值，≥0.5的为一个类别，<0.5为另外一个类别。这个例子说明，线性回归依然可以用来解决分类问题。但是，看下面的例子，结论就不一样了。

对比逻辑回归和线性回归在解决分类问题时的差异2

/如上图，增加了1个sample。线性规划拟合出来的直线为蓝色的线，而不再是之前的红色的直线。
蓝色的直线将使得threshhold(x)=0.5阈值点右移，变得不再准确了。
所以，分类问题，适合使用逻辑回归并不适合使用线性回归。

对比逻辑回归和线性回归在解决分类问题时的差异3

如上图，因为线性回归的预测值可能会>1或者<0，所以线性回归不好。而逻辑回归的预测值会严格控制在[0,1]，所以采用逻辑回归去解决0-1分类问题。
Logistic Regression(逻辑回归)和通常意义上的”逻辑”没什么关系，只是一个名称的音译而已。

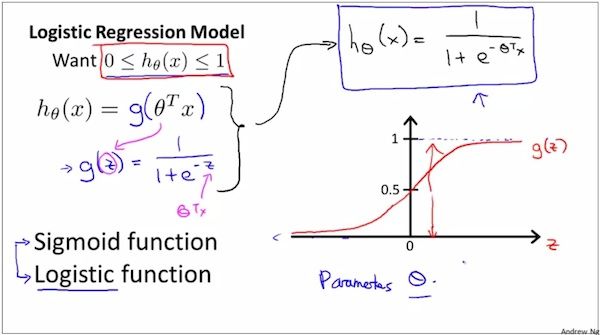
逻辑回归模型的数学表达式

如上图，Logistic Function是逻辑回归的模型，直观地说，也就是函数表达式。这个函数表达式能够使得这个函数的取值范围在(0,1)，所以满足我们之前对0-1分类问题的期待。

补充说明一下，因为y=exp(x)的取值范围是(0, 正无穷)，如上图所示，
所以，Sigmoid Function才有了上图所示的形状，才能取值范围在(0,1)

该如何理解逻辑回归模型的输出

如上图的的定义，从概率角度理解逻辑回归的输出的含义

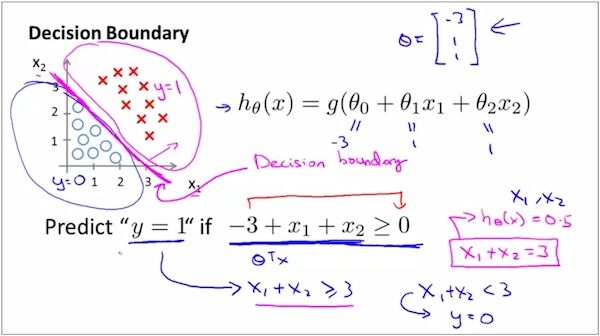
逻辑回归的Decision Boundary - 1

如上图，红线是Decision Boundary
1) 直观地看，如果一条线能够将样本正好划分为两类，这条线就是Decision Boundary。
2) 这条线是如何求出来的呢?
    hθ(x)=0.5是样本类型的分界点
    由Sigmoid Function的表达式知，x=0是样本类型的分界点，即直线θ₀+θ₁x₁+θ₂x₂=0为样本类型的分界点
    假设 θ取值为
            [ -3,
theta=    1,
             1 ]
    那么直线-3+x₁+x₂=0为样本分界点。
    那么也就是图中的红线了。
3) 注意，从上面的过程可以看出，分界线是与θ的特定的取值相关的，是θ的属性，而不是训练数据集的属性。

逻辑回归的Decision Boundary-2

如上图，这里的decision boundary不是一条直线，而是一个圆形了。为什么呢？
因为这里的θ(x)中的x不再是上上例那样的一个简单的线性表达式了，而是一个2元2次多项式。
找寻分界点的过程类似上上例，Hθ(x)=0.5是分界点，所以x=0是分界点，所以上面的2元2次多项式=0是分界点，化简后得到上图所示圆形。
同样注意，decision boundary is not the properties of the training data, but the properties of the hypothesis of the parameter. While the training data is used to train the parameter.

逻辑回归的Decision Boundary-3

类似地，可以Decision Boundary的形状决定于Hθ(x)是几元几次。如果Hθ(x)非常复杂，那么Decision Boundary的形状也会变得相应地复杂。

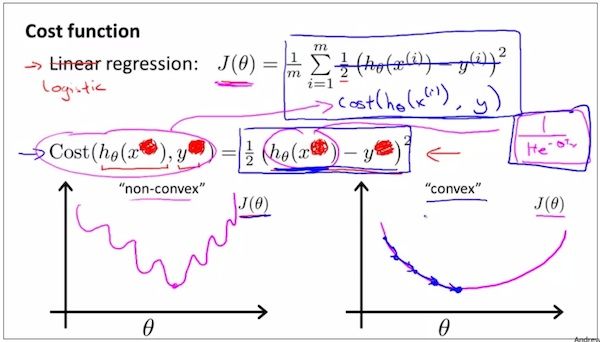
训练-如何找到合适的parameters to automatically fit the training data

如上，类比线性回归的定义，这里定义了逻辑回归的cost function。

如上，为了简化，写成为上图的形式。

但是，从线性回归类比而得到的逻辑回归的cost function存在一个问题。这个cost function可能不是凸函数，所以不能保证每次得出的局部最优也是全局最优。
所以现在需要为逻辑回归找寻另外的cost function，从而使得逻辑回归的cost function也是凸函数。如下。

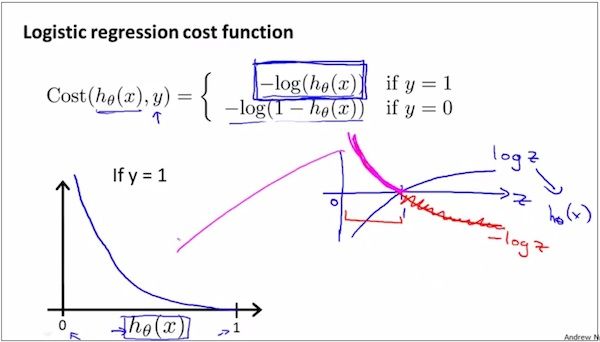
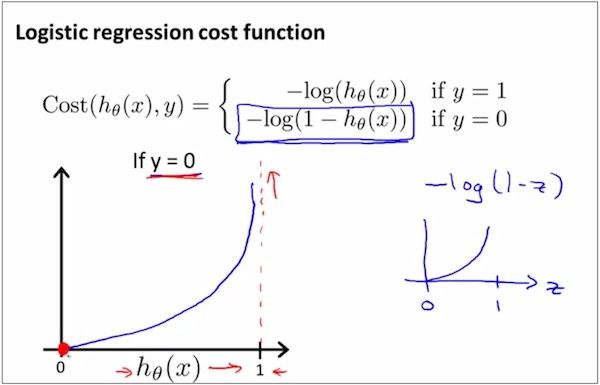
如上，Logistic Regression 的cost function的定义，这是当y=1时候的情况。可以先体会(0,+∞)点和(1,0)这两个端点的情况

如上，Logistic Regression 的Cost Function的定义，这是当y=0时候的情况，看图体会为什么是这样的变化趋势，可以先体会(0,0)点和(1,+∞)这两个端点的情况。

简化Logistic Regression的cost function的表达式1

简化Logistic Regression的cost function的表达式2

用梯度下降求cost function的最小值

如上图，
1 看上去线性回归进行Gradient Descent的表达式和逻辑回归进行Gradient Descent的表达式是一样的形式。但是其实是不一样的，逻辑回归的hθ(x)和线性回归的hθ(x)不一样。逻辑回归的hθ(x)表达式如红色计算式所示，线性回归的hθ(x)表达式如蓝色计算式所表示。

Optimization
1 Feature scaling in Logistic Regression can help to fasten the speed of Gradient Descent in Logistic Regression, like that in Linear Regression.
2 introduce some ways of optimization to fasten Gradient Descent of Logistic Regression

Optimization—目标1

求Optima的其它途径-Advanced Optimization Algorithm

如上，如果已知J(theta) 和J(theta)对thetaj的偏导数，那么求cost function的最小值的算法除了Gradient Descent，还有另外三种，Conjugate Gradient, BFGS, L-BFGS

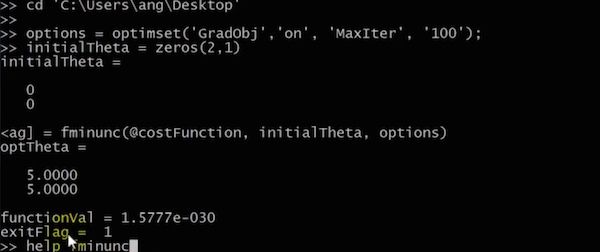
Ocatave中使用Advanced Optimization Algorithm的一个例子

Ocatave中的如何使用Advanced Optimization Algorithm执行Logistic Regression?

说明，使用advanced optimization algorithm执行logistic regression的时候，由于用到了一些复杂的Library，所以代码比较晦涩，但是它们能够比Gradient Descent更加快速。

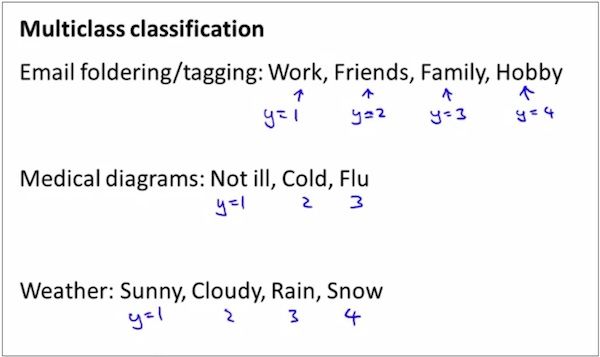
Multi-class Classifications-任务是什么？

 类比思维: Using the idea of one-vs-all(one-vs-rest) classification, we can do multi-class classification as well.

Multi-class Classifications-类比思维解决Multi-class Classification问题

如上，有N个类，就训练N次。每次训练都是一次binary classification过程

如上，预测阶段，计算x成为所有class中得每一种class对应的概率，找到最大概率对应的class。 


Overfitting
what is overfitting?例1

what is overfitting?例2

How to reduce it? regulation1

如上，如何减少overfitting。接下来会讲到如何automatically decide which feature to select and which feature to keep.

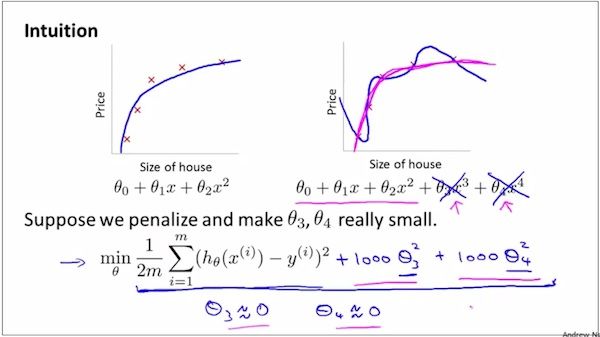
How to reduce it? regulation-2

如上，看一个例子，直观地感受下如何增加惩罚因子从而降低overfitting.

How to reduce it? regulation-3

如上，从上上图的例子可知，Regularization就是增加惩罚因子，使得parameters尽可能小，从而避免overfitting
注意1  为什么减小parameters就可以避免overfitting，以后再讲。
注意2 一般的做法是，尽可能第减少θ₀之外的所有θ。
注意3 Regularized logistic regression and regularized linear regression are both convex, and thus gradient descent will still converge to the global minimum.
注意4 物极必反。If we introduce too much regularization, we can underfit the training set and this can lead to worse performance even for examples not in the training set

How to reduce it? regulation-4

如上，λ is used to control the tradeoff between keeping the parameters small and finding the optima of the cost function.

How to reduce it? regulation-4 如果λ太大也不好会造成underfitting

How to know that overfitting happens? (以后章节介绍)

使用Regularized Gradient Descent  for Linear Regression

使用数学优化办法Normal Equation for Linear Regression求θ — 假设没有regulation

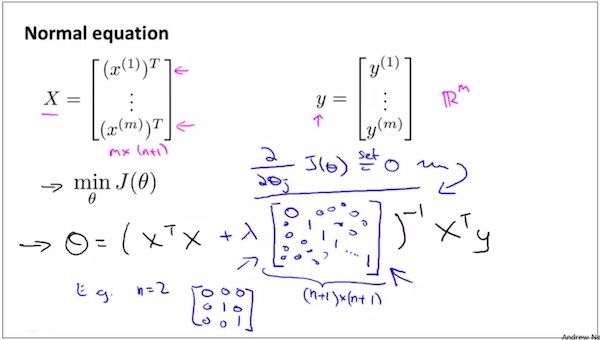
使用数学优化办法Normal Equation for Linear Regression 求 θ— 假设有regulation

使用数学优化办法Normal Equation for Logistic Regression 求 θ— 假设有regulation

使用Regularized Gradient Descent for Logistic Regression 求 θ 假设有regulation

使用Advanced Optimization for Logistic Regression

现在来解决一开始的几个问题。

1 为什么广告预测点击率使用的是逻辑回归模型? 

   因为首先这是个分类问题，适合是逻辑回归。其次，虽然线性回归也勉强能够用来拟合分类问题，但是误差会非常大。

2 当有多个输入变量可能对输出结果造成影响时，如何判断谁的相关性最大？ 

   训练后得出的系数中，最大的系数对应的特征(输入变量)对结果造成的影响最大。

3 输入变量和输出结果是因果关系还是相关关系，这个该如何判断?

   Machine Learning课目前不能解决这个问题

4 多个输入变量之间有因果关系和没有因果关系时，对输出结果的影响有什么区别? 

   Machine Learning课目前不能解决这个问题

5 octave内自带的fimunc()是如何进行优化的？使用了梯度下降进行优化吗？

  fimunc的用来求minimun, 它在官方帮助中写明了，可以使用梯度下降进行优化，也可以使用其它办法。本章求logistic regression 的最小值，使用了fimunc搭配梯度下降的方法。