Josephus问题及其推广 分析和算法优化
具体实现请见 http://blog.csdn.net/hnust_V/article/details/51747212
问题 C,D,I: Josephus问题
题目描述
n个人排成一圈,按顺时针方向依次编号1,2,3…n。从编号为1的人开始顺时针”一二”报数,报到m的人退出圈子。这样不断循环下去,圈子里的人将不断减少。最终一定会剩下一个人。试问最后剩下的人的编号。
输入
C,D:每组数据一行,每行一个正整数,代表人数n。 (1 <= n < k)
I:每组数据一行,每行两个正整数,为 n和m。 (1 <= n < k)
//C : k=1000,C,D m=2
//D,I: k=2^31
输出
每组输入数据输出一行, 仅包含一个整数,代表最后剩下的人的编号。
报告:
其中C题是属于数据结构应用范畴的,但是D,I题问题上界表明只能使用数学方法
先给出 C题的利用数据结构模拟法,因为是一个圈,所以考虑到用循环队列
请先实现 数据结构queue 的功能 或 使用C++ 中的STL
Cal(n, Que): //Que 为int型队列
for i=1 to n
Que.push(i); //将编号1~n的人放入队列
Count=0
while Que.size() >1 //踢人直到剩余一个
Count = Count +1
if Count%2=0 //报号为2
Que.pop(); //踢出
else //报号为1 则从队列中取出再放入对尾
a=Que.front()
Que.pop()
Que.push(a)
return Que.front()可用于C,D的数学写法:
/以下内容引用了<<具体数学>> &1.4 约瑟夫问题 中部分数学知识/
m=2时 :
数学规律1:【是经过严格推导的】
有 f(2n+1)=2f(n)+1 ; f(2n)=2f(n)-1 ; f(1)=1
数学规律 2:【是由规律1所得】
将n表达成二进制 m ,m左循环一位便为答案
利用规律1: //若用C/C++ 请使用long long 实现
Cal(n):
If n=1
return 1
if n%2=0 //偶数n
return Cal(n/2)*2-1
else
return Cal((n-1)/2)*2+1规律2同样易实现,此处不赘述
/以上内容引用了<<具体数学>> &1.4 约瑟夫问题 中部分数学知识/
但是对于I题 ( 约瑟夫问题的推广 ),解决本题,必须先对约瑟夫问题有根本上的理解
分析:

首先,第一个出圈者编号必定为 m % n
令k = m % n+1,于是图等价为(a),再对k,k+1……k-2 重新标号1~n-1 便为图(b)

我们可以发现前后的标号编号规则,计F(n)为n人组成的圈里编号
F(n) F(n-1)
K 1
K+1 2
K+2 3
.... ....
k-2 n-1
k-1 n 被剔除
很容易得到变化规律:
F(n) = [F(n-1)+k(n)-1] % n
k(n) = m % n + 1 //见上面
重新考虑 n-1人圈,很明显这是一个与n人圈的相同小规模子问题
由此递推下去 n-2,n-3,……,1 人圈是同类问题
而1人圈很明显 F(1)=1 //这货就是剩余者
我们又有序号变化规律(序号的状态转移方程),完全可以一步步推到这货在n人圈里的序号,问题便这样解决了
综上所述
k(n) = m % n + 1
F(n) = [F(n-1)+k(n)-1] % n
F(1)=1
再将k(n)带入式2有
F(n) = [F(n-1)+m % n] % n = [F(n-1)+m] % n
F(1)=1
这便是最终结论,也是I题求解的基础
给出结论两种实现
递归实现:
Cal(n,m):
if n=1
return 1
else
ans = [Cal(n-1,m)+m]%n
if ans=0
ans = n 第0个应当为当前第n个
return ans递推实现:
Cal(n,m):
ans = 1
for i = 1 to n
ans = (ans+m) %i
if ans = 0
ans = n
return ans但是!即使O(n)的运算速度仍然不能AC该题,我们需要优化!
/以下算法由大牛们的博客提供了优化方向Orz,但不知具体是那位牛首先提出该优化策略,故此处不提供博客链接/
首先递归算法必然不能使用 //2^31必然会栈溢
考虑在递推上进行优化
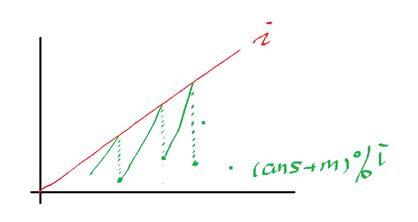
对于 ans = (ans+m) %i,如图可以发现当ans+m >= i时,ans即将被取余而不大于i,而当ans+m < i时 (ans+m) %i = ans+m
而 ans+m+m < i+1 仍然成立的话,甚至 ans+x*m < i+x-1都在成立,那么完全可以视为一个从 ans 开始增长的等差数列
令x为满足 ans+x*m < i+x-1的最大值
然后我们直接让ans变为ans+x*m,i直接增到i+x 从而跳过x-1步,得到优化,当然如果 i+x>n 那么ans+(n-(i-1))*m 就应当得解,此时正是第n人圈
那么对于n>m的情况下复杂度仅为O(m),
那么为什么是O(m)? 提示 :因为每次比m大时总会被对m取余
//给出伪代码请用long long实现
Cal(n,m):
ans = 1,i=1
if m = 1 //这里既是优化,也是完善不足->m=1时始终有ans+m>=i
return n;//原理很简单 n个人报1退出,前n-1个都因报1被踢出
while i<=n
if ans+m < i //被优化的部分
x = (i-1-ans)/(m-1)
if x=0 //这里防止x恰好是m-1的倍数
x = (i-1-ans)/(m-1)-1;
if i+x > n
ans = ans + (n+1-i)*m;
break
else
ans = ans + x*m
i = i + x
else //正常的递推
ans = (ans+m)%i
if ans = 0
ans = i
i=i+1
return ans
最后让我们再次膜拜一下大牛们的神一般思路Orz
