深度学习课后作业——Course2-Week3

此篇摘自*这个巨巨*，本文只是加上了自己的总结

---

• 深度学习里的Xavier初始化

“Xavier”初始化方法是一种很有效的神经网络初始化方法，方法来源于2010年的一篇论文《Understanding the difficulty of training deep feedforward neural networks》。文章主要的目标就是使得每一层输出的方差应该尽量相等。

定义参数所在层的输入维度为n，输出维度为m，那么参数将以均匀分布的方式在的范围内进行初始化。tf

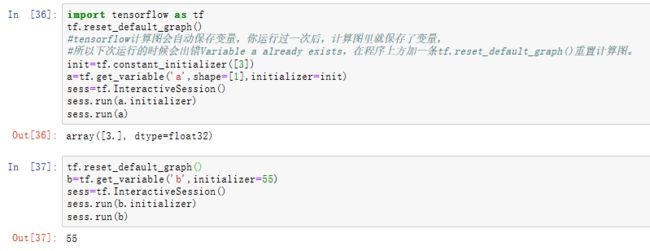
• tf.get_variable 与tf.Variable

tf.Variable()用于生成一个初始值为initial-value的变量；必须指定初始化值。

tf.get_variable()获取已存在的变量(要求不仅名字，而且初始化方法等各个参数都一样)，如果不存在，就新建一个；可以用各种初始化方法，不用明确指定值。

tf.get_variable函数的使用

tf.get_variable(name,  shape, initializer): name就是变量的名称，shape是变量的维度，initializer是变量初始化的方式，初始化的方式有以下几种：

tf.constant_initializer：常量初始化函数

tf.random_normal_initializer：正态分布

tf.truncated_normal_initializer：截取的正态分布

tf.random_uniform_initializer：均匀分布

tf.zeros_initializer：全部是0

tf.ones_initializer：全是1

tf.uniform_unit_scaling_initializer：满足均匀分布，但不影响输出数量级的随机值

• 独热编码（one-hot encoding） 摘自

一、问题由来

在很多机器学习任务中，特征并不总是连续值，而有可能是分类值。

离散特征的编码分为两种情况：

　　1、离散特征的取值之间没有大小的意义，比如color：[red,blue],那么就使用one-hot编码

　　2、离散特征的取值有大小的意义，比如size:[X,XL,XXL],那么就使用数值的映射{X:1,XL:2,XXL:3}

使用pandas可以很方便的对离散型特征进行one-hot编码

例如，考虑一下的三个特征：

["male", "female"]

["from Europe", "from US", "from Asia"]

["uses Firefox", "uses Chrome", "uses Safari", "uses Internet Explorer"]

如果将上述特征用数字表示，效率会高很多。例如：

["male", "from US", "uses Internet Explorer"] 表示为[0, 1, 3]

["female", "from Asia", "uses Chrome"]表示为[1, 2, 1]

但是，即使转化为数字表示后，上述数据也不能直接用在我们的分类器中。因为，分类器往往默认数据数据是连续的（可以计算距离？），并且是有序的（而上面这个0并不是说比1要高级）。但是，按照我们上述的表示，数字并不是有序的，而是随机分配的。

独热编码

为了解决上述问题，其中一种可能的解决方法是采用独热编码（One-Hot Encoding）。独热编码即 One-Hot 编码，又称一位有效编码，其方法是使用N位状态寄存器来对N个状态进行编码，每个状态都由他独立的寄存器位，并且在任意时候，其中只有一位有效。

例如：

自然状态码为：000,001,010,011,100,101

独热编码为：000001,000010,000100,001000,010000,100000

可以这样理解，对于每一个特征，如果它有m个可能值，那么经过独热编码后，就变成了m个二元特征（如成绩这个特征有好，中，差变成one-hot就是100, 010, 001）。并且，这些特征互斥，每次只有一个激活。因此，数据会变成稀疏的。

这样做的好处主要有：

1. 解决了分类器不好处理属性数据的问题

2. 在一定程度上也起到了扩充特征的作用

tensorflow里只要一行代码：

tf.one_hot(labels,depth,axis)

•  tf.nn.softmax_cross_entropy_with_logits摘自

tf.nn.softmax_cross_entropy_with_logits(
    _sentinel=None,
    labels=None,
    logits=None,
    dim=-1,
    name=None
)

这个函数的功能就是计算labels和logits之间的交叉熵（cross entropy）。

第一个参数基本不用。此处不说明。
第二个参数label的含义就是一个分类标签，所不同的是，这个label是分类的概率，比如说[0.2,0.3,0.5]，labels的每一行必须是一个概率分布（即概率之合加起来为1）。

现在来说明第三个参数logits，logit的值域范围[-inf,+inf]（即正负无穷区间）。我们可以把logist理解为原生态的、未经缩放的，可视为一种未归一化的l“概率替代物”，如[4, 1, -2]。它可以是其他分类器（如逻辑回归等、SVM等）的输出。

例如，上述向量中“4”的值最大，因此，属于第1类的概率最大，“1”的值次之，所以属于第2类的概率次之。

交叉熵（Cross Entropy）是Shannon信息论中一个重要概念，主要用于度量两个概率分布间的差异性信息。

由于logis本身并不是一个概率，所以我们需要把logist的值变化成“概率模样”。这时Softmax函数该出场了。Softmax把一个系列的概率替代物（logits）从[-inf, +inf] 映射到[0,1]。除此之外，Softmax还保证把所有参与映射的值累计之和等于1，变成诸如[0.95, 0.05, 0]的概率向量。

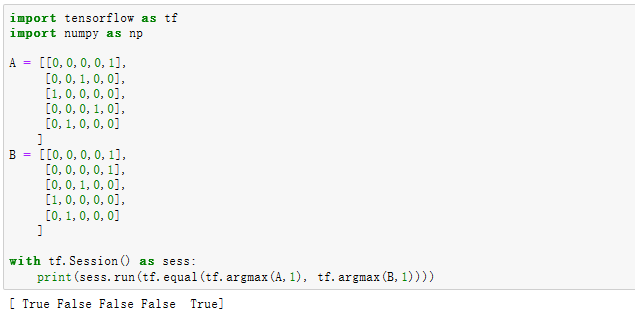
• tf.equal(tf.argmax(y, 1),tf.argmax(y_, 1))

tf.argmax(vector, 1)
返回的是vector中的最大值的索引号，如果vector是一个向量，那就返回一个值，如果是一个矩阵，那就返回一个向量，这个向量的每一个维度都是相对应矩阵行的最大值元素的索引号。

tf.equal(A, B)是对比这两个矩阵或者向量的相等的元素，如果是相等的那就返回True，否则返回False，返回的值的矩阵维度和A是一样的。

• tf.cast 、tf.reduce_mean

tf.cast:

强制类型转换，将data_1(可以为int，bool，float,python列表，python元组【输出转换后的数据,原数据不变】）转换成指定dtype类型
tf.reduce_mean()：

求输入数据的平均值

---

代码整合：

import numpy as np
import h5py
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
import tf_utils
import time
X_train_orig , Y_train_orig , X_test_orig , Y_test_orig , classes = tf_utils.load_dataset()
X_train_flatten = X_train_orig.reshape(X_train_orig.shape[0],-1).T #每一列就是一个样本
X_test_flatten = X_test_orig.reshape(X_test_orig.shape[0],-1).T

#归一化数据
X_train = X_train_flatten / 255
X_test = X_test_flatten / 255

#转换为独热矩阵
Y_train = tf_utils.convert_to_one_hot(Y_train_orig,6)
Y_test = tf_utils.convert_to_one_hot(Y_test_orig,6)

#%matplotlib inline #如果你使用的是jupyter notebook取消注释
np.random.seed(1)


def linear_function():
    """
    实现一个线性功能：
        初始化W，类型为tensor的随机变量，维度为(4,3)
        初始化X，类型为tensor的随机变量，维度为(3,1)
        初始化b，类型为tensor的随机变量，维度为(4,1)
    返回：
        result - 运行了session后的结果，运行的是Y = WX + b 
    
    """
    
    np.random.seed(1) #指定随机种子
    
    X = np.random.randn(3,1)
    W = np.random.randn(4,3)
    b = np.random.randn(4,1)
    
    Y = tf.add(tf.matmul(W,X),b) #tf.matmul是矩阵乘法
    #Y = tf.matmul(W,X) + b #也可以以写成这样子
    
    #创建一个session并运行它
    sess = tf.Session()
    result = sess.run(Y)
    
    #session使用完毕，关闭它
    sess.close()
    
    return result

def sigmoid(z):
    """
    实现使用sigmoid函数计算z
    
    参数：
        z - 输入的值，标量或矢量
    
    返回：
        result - 用sigmoid计算z的值
    
    """
    
    #创建一个占位符x，名字叫“x”
    x = tf.placeholder(tf.float32,name="x")
    
    #计算sigmoid(z)
    sigmoid = tf.sigmoid(x)
    
    #创建一个会话，使用方法二
    with tf.Session() as sess:
        result = sess.run(sigmoid,feed_dict={x:z})
        
    return result

def one_hot_matrix(lables,C):
    """
    创建一个矩阵，其中第i行对应第i个类号，第j列对应第j个训练样本
    所以如果第j个样本对应着第i个标签，那么entry (i,j)将会是1
    
    参数：
        lables - 标签向量
        C - 分类数
        
    返回：
        one_hot - 独热矩阵
    
    """
    
    #创建一个tf.constant，赋值为C，名字叫C
    C = tf.constant(C,name="C")
    
    #使用tf.one_hot，注意一下axis
    one_hot_matrix = tf.one_hot(indices=lables , depth=C , axis=0)
    
    #创建一个session
    sess = tf.Session()
    
    #运行session
    one_hot = sess.run(one_hot_matrix)
    
    #关闭session
    sess.close()
    
    return one_hot

def ones(shape):
    """
    创建一个维度为shape的变量，其值全为1
    
    参数：
        shape - 你要创建的数组的维度
    
    返回：
        ones - 只包含1的数组    
    """
    
    #使用tf.ones()
    ones = tf.ones(shape)
    
    #创建会话
    sess = tf.Session()
    
    #运行会话
    ones = sess.run(ones)
    
    #关闭会话
    sess.close()
    
    return ones

def create_placeholders(n_x,n_y):
    """
    为TensorFlow会话创建占位符
    参数：
        n_x - 一个实数，图片向量的大小（64*64*3 = 12288）
        n_y - 一个实数，分类数（从0到5，所以n_y = 6）
    
    返回：
        X - 一个数据输入的占位符，维度为[n_x, None]，dtype = "float"
        Y - 一个对应输入的标签的占位符，维度为[n_Y,None]，dtype = "float"
    
    提示：
        使用None，因为它让我们可以灵活处理占位符提供的样本数量。事实上，测试/训练期间的样本数量是不同的。
    
    """
    
    X = tf.placeholder(tf.float32, [n_x, None], name="X")
    Y = tf.placeholder(tf.float32, [n_y, None], name="Y")
    
    return X, Y

def initialize_parameters():
    """
    初始化神经网络的参数，参数的维度如下：
        W1 : [25, 12288]
        b1 : [25, 1]
        W2 : [12, 25]
        b2 : [12, 1]
        W3 : [6, 12]
        b3 : [6, 1]
    
    返回：
        parameters - 包含了W和b的字典
    
    
    """
    
    tf.set_random_seed(1) #指定随机种子
    
    W1 = tf.get_variable("W1",[25,12288],initializer=tf.contrib.layers.xavier_initializer(seed=1))
    b1 = tf.get_variable("b1",[25,1],initializer=tf.zeros_initializer())
    W2 = tf.get_variable("W2", [12, 25], initializer = tf.contrib.layers.xavier_initializer(seed=1))
    b2 = tf.get_variable("b2", [12, 1], initializer = tf.zeros_initializer())
    W3 = tf.get_variable("W3", [6, 12], initializer = tf.contrib.layers.xavier_initializer(seed=1))
    b3 = tf.get_variable("b3", [6, 1], initializer = tf.zeros_initializer())
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2,
                  "W3": W3,
                  "b3": b3}
    
    return parameters

def forward_propagation(X,parameters):
    """
    实现一个模型的前向传播，模型结构为LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAX
    
    参数：
        X - 输入数据的占位符，维度为（输入节点数量，样本数量）
        parameters - 包含了W和b的参数的字典
    
    返回：
        Z3 - 最后一个LINEAR节点的输出
    
    """
    
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    W3 = parameters['W3']
    b3 = parameters['b3']
    
    Z1 = tf.add(tf.matmul(W1,X),b1)        # Z1 = np.dot(W1, X) + b1
    #Z1 = tf.matmul(W1,X) + b1             #也可以这样写
    A1 = tf.nn.relu(Z1)                    # A1 = relu(Z1)
    Z2 = tf.add(tf.matmul(W2, A1), b2)     # Z2 = np.dot(W2, a1) + b2
    A2 = tf.nn.relu(Z2)                    # A2 = relu(Z2)
    Z3 = tf.add(tf.matmul(W3, A2), b3)     # Z3 = np.dot(W3,Z2) + b3
    
    
    return Z3
    

def compute_cost(Z3,Y):
    """
    计算成本
    
    参数：
        Z3 - 前向传播的结果
        Y - 标签，一个占位符，和Z3的维度相同
        
    返回：
        cost - 成本值
    
    
    """
    logits = tf.transpose(Z3) #转置
    labels = tf.transpose(Y)  #转置
    
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits,labels=labels))
    
    return cost


    
def model(X_train,Y_train,X_test,Y_test,
		learning_rate=0.0001,num_epochs=1500,minibatch_size=32,
		print_cost=True,is_plot=True):
    """
    实现一个三层的TensorFlow神经网络：LINEAR->RELU->LINEAR->RELU->LINEAR->SOFTMAX
    
    参数：
        X_train - 训练集，维度为（输入大小（输入节点数量） = 12288, 样本数量 = 1080）
        Y_train - 训练集分类数量，维度为（输出大小(输出节点数量) = 6, 样本数量 = 1080）
        X_test - 测试集，维度为（输入大小（输入节点数量） = 12288, 样本数量 = 120）
        Y_test - 测试集分类数量，维度为（输出大小(输出节点数量) = 6, 样本数量 = 120）
        learning_rate - 学习速率
        num_epochs - 整个训练集的遍历次数
        mini_batch_size - 每个小批量数据集的大小
        print_cost - 是否打印成本，每100代打印一次
        is_plot - 是否绘制曲线图
    
    返回：
        parameters - 学习后的参数

    """
    ops.reset_default_graph()                #能够重新运行模型而不覆盖tf变量
    tf.set_random_seed(1)
    seed = 3
    (n_x , m)  = X_train.shape               #获取输入节点数量和样本数
    n_y = Y_train.shape[0]                   #获取输出节点数量
    costs = []                               #成本集
    
    #给X和Y创建placeholder
    X,Y = create_placeholders(n_x,n_y)
    
    #初始化参数
    parameters = initialize_parameters()
    
    #前向传播
    Z3 = forward_propagation(X,parameters)
    
    #计算成本
    cost = compute_cost(Z3,Y)
    
    #反向传播，使用Adam优化
    optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
    
    #初始化所有的变量
    init = tf.global_variables_initializer()
    
    #开始会话并计算
    with tf.Session() as sess:
        #初始化
        sess.run(init)
        
        #正常训练的循环
        for epoch in range(num_epochs):
            
            epoch_cost = 0  #每代的成本
            num_minibatches = int(m / minibatch_size)    #minibatch的总数量
            seed = seed + 1
            minibatches = tf_utils.random_mini_batches(X_train,Y_train,minibatch_size,seed)
            
            for minibatch in minibatches:
                
                #选择一个minibatch
                (minibatch_X,minibatch_Y) = minibatch
                
                #数据已经准备好了，开始运行session
                _ , minibatch_cost = sess.run([optimizer,cost],feed_dict={X:minibatch_X,Y:minibatch_Y})
                
                #计算这个minibatch在这一代中所占的误差
                epoch_cost = epoch_cost + minibatch_cost / num_minibatches
                
            #记录并打印成本
            ## 记录成本
            if epoch % 5 == 0:
                costs.append(epoch_cost)
                #是否打印：
                if print_cost and epoch % 100 == 0:
                        print("epoch = " + str(epoch) + "    epoch_cost = " + str(epoch_cost))
        
        #是否绘制图谱
        if is_plot:
            plt.plot(np.squeeze(costs))
            plt.ylabel('cost')
            plt.xlabel('iterations (per tens)')
            plt.title("Learning rate =" + str(learning_rate))
            plt.show()
        
        #保存学习后的参数
        parameters = sess.run(parameters)
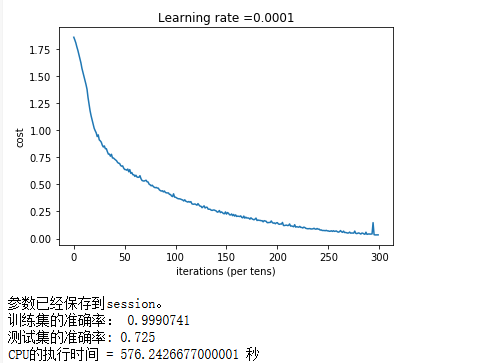
        print("参数已经保存到session。")
        
        #计算当前的预测结果
        correct_prediction = tf.equal(tf.argmax(Z3),tf.argmax(Y))
        
        #计算准确率
        accuracy = tf.reduce_mean(tf.cast(correct_prediction,"float"))
        
        print("训练集的准确率：", accuracy.eval({X: X_train, Y: Y_train}))
        print("测试集的准确率:", accuracy.eval({X: X_test, Y: Y_test}))
        
        return parameters
    
#开始时间
start_time = time.clock()
#开始训练
parameters = model(X_train, Y_train, X_test, Y_test)
#结束时间
end_time = time.clock()
#计算时差
print("CPU的执行时间 = " + str(end_time - start_time) + " 秒" )

执行结果：