C#中的寻路算法
目录
介绍
问题
Dijkstra算法
A *算法
结果
结论
挑战
Dijkstra和Astar的比较
Download source - 571.3 KB
在Visual Studio 2017中解压缩并打开解决方案
介绍
你有没有想过GPS应用程序如何计算到选定目的地的最快方式?正如您将看到的,它实际上非常简单。
本文将对此进行说明并提供您可以随意使用的示例代码。本文还比较了两种常见的基本算法,Dijkstra和A *。
问题
假设你有一张地图。你知道你在哪里以及你想去哪里。地图具有连接节点(具有坐标的位置)的道路(它们被称为边)。
从每个节点,您可以转到一个或多个边。边是具有成本的(例如,旅行所需的路程长度或时间)。对于小地图,可以计算到目的地的所有可能路线并选择最短路线。但是对于具有许多节点的地图来说,这不是很实用,因为组合会呈指数级增长。
Dijkstra算法
Dijkstra算法于1959年由Edsger Dijkstra发现。这是它的工作原理:
- 从起始节点,将所有连接的节点添加到优先级队列。
- 按最低成本对优先级队列进行排序,并将第一个节点作为当前节点。
对于每个子节点,选择导致最短路径到开始节点的最佳节点。
当从一个节点调查所有边时,该节点为“ Visited”,您不需要再次访问该节点。 - 将连接到当前节点的每个子节点添加到优先级队列。
- 转到步骤2,直到队列为空。
- 递归地创建从最开始到结束的最短路径的每个节点的节点列表。
- 反转列表,您找到了最短的路径
换句话说,递归地为节点的每个子节点测量它到开始节点的距离。存储距离和存储导致到开始节点最短路径的节点。当你到达终点节点时,递归地以最短的路径返回到开始节点,反转该列表并且你将拥有最短的路径。
下面是我在C#代码中的Dijkstra算法实现。它可能比上面更容易理解。
public List GetShortestPathDijkstra()
{
DijkstraSearch();
var shortestPath = new List();
shortestPath.Add(End);
BuildShortestPath(shortestPath, End);
shortestPath.Reverse();
return shortestPath;
}
private void BuildShortestPath(List list, Node node)
{
if (node.NearestToStart == null)
{
return;
}
list.Add(node.NearestToStart);
BuildShortestPath(list, node.NearestToStart);
}
private void DijkstraSearch()
{
Start.MinCostToStart = 0;
var prioQueue = new List();
prioQueue.Add(Start);
do {
prioQueue = prioQueue.OrderBy(x => x.MinCostToStart).ToList();
var node = prioQueue.First();
prioQueue.Remove(node);
foreach (var cnn in node.Connections.OrderBy(x => x.Cost))
{
var childNode = cnn.ConnectedNode;
if (childNode.Visited)
{
continue;
}
if (childNode.MinCostToStart == null ||
node.MinCostToStart + cnn.Cost < childNode.MinCostToStart)
{
childNode.MinCostToStart = node.MinCostToStart + cnn.Cost;
childNode.NearestToStart = node;
if (!prioQueue.Contains(childNode))
{
prioQueue.Add(childNode);
}
}
}
node.Visited = true;
if (node == End)
{
return;
}
} while (prioQueue.Any());
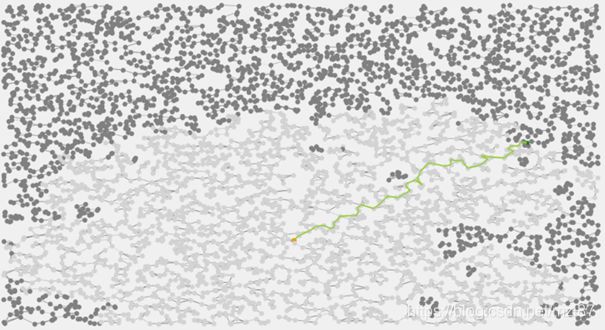
} 这是我测试程序中随机生成的地图。点是节点,它们之间是表示边的线。该地图由5000个节点和15000个边组成。
搜索算法访问较浅的彩色点,最佳路径以绿色绘制。
A *算法
Dijkstra算法有很多改进。其中最常见的是A *。它与Dijkstra基本相同,只有一个简单的修改。
边的优先级也取决于边与目标的直线距离有多近。因此,在运行A *搜索之前,必须为每个节点测量出到最终目的地的直线距离,如果您知道每个节点的坐标,这很容易。这是A *的最简单形式,其定义也允许对启发式函数的改进。(在本例中为StraightLineDistanceToEnd)
该算法具有很大的性能优势,因为当终点的路径的方向已知时,它不需要访问尽可能多的节点。
请参阅下面的实现。
public List GetShortestPathAstar()
{
foreach (var node in Map.Nodes)
{
node.StraightLineDistanceToEnd = node.StraightLineDistanceTo(End);
}
AstarSearch();
var shortestPath = new List();
shortestPath.Add(End);
BuildShortestPath(shortestPath, End);
shortestPath.Reverse();
return shortestPath;
}
private void AstarSearch()
{
Start.MinCostToStart = 0;
var prioQueue = new List();
prioQueue.Add(Start);
do {
prioQueue = prioQueue.OrderBy(x => x.MinCostToStart + x.StraightLineDistanceToEnd).ToList();
var node = prioQueue.First();
prioQueue.Remove(node);
NodeVisits++;
foreach (var cnn in node.Connections.OrderBy(x => x.Cost))
{
var childNode = cnn.ConnectedNode;
if (childNode.Visited)
{
continue;
}
if (childNode.MinCostToStart == null ||
node.MinCostToStart + cnn.Cost < childNode.MinCostToStart)
{
childNode.MinCostToStart = node.MinCostToStart + cnn.Cost;
childNode.NearestToStart = node;
if (!prioQueue.Contains(childNode))
{
prioQueue.Add(childNode);
}
}
}
node.Visited = true;
if (node == End)
{
return;
}
} while (prioQueue.Any());
} 这与上面的地图相同,但路径是使用A *算法计算的。如您所见,需要访问的节点要少得多。
结果
在同一个500,000个节点的地图上运行这两种算法时,我得到了这些结果。
|
|
Dijkstra算法 |
A* |
| 访问过的节点 |
330871 |
19410 |
| 计算时间(ms) |
850 |
127 |
| 最佳路径的成本 |
14322 |
22994 |
| 最短路径的距离 |
0,82446 |
0,82446 |
正如您在上表中所看到的,A *算法比Dijkstra快约7倍,并且它们都找到了最短的路径。
但是,当为边的成本生成随机数时,Dijkstra找到一个较低成本的路径。例如,在实际地图中,最短路径并不总是最好的。在速度限制较高的道路上行驶可能会让您更快到达目的地。这就是为什么在边成本中添加随机数使得这个实验更加真实。
结论
那么什么算法是Dijkstra和A *的最佳路径寻找算法?
我认为这要视情况而定。如果您只对最短路径感兴趣,那就是A *。
速度要快得多,它与Dijkstra的效果相同。但是如果边成本还有其他方面的长度,那么Dijkstra在寻找最佳路径方面比这个版本的A *更好。毕竟,它仍然非常快。我认为500,000个节点是一个非常大的数据集。我也认为我的实现可以进行很多优化。
挑战
如果你还天真地喜欢编程挑战,也许你想给机器人编程,让它走出迷宫?
您可能需要一些路径查找算法来解决它。
参考这个网站:http://airobots.azurewebsites.net/
感谢阅读,我希望你发现路径查找算法和我现在一样有趣。
祝你今天愉快!
原文地址:https://www.codeproject.com/Articles/1221034/Pathfinding-Algorithms-in-Csharp