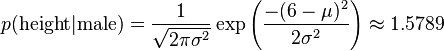朴素贝叶斯模型(Naive Bayes Model,NB)理解
1. Bayes 定理
- P(A,B)=P(A|B)P(B);
- P(A,B)=P(B|A)P(A);
- P(A|B)=P(B|A)P(A)/P(B); 贝叶斯定理变形
2. 概率图模型
2.1 定义
2.2 随机变量的条件独立
如果有P(A,B|C)=P(A|C)P(B|C), 则称在给定事件C的条件下,两个事件A和B独立,这里假设P(C)>0;
如:设A=2x+z; B=y+z; C=z;
在C确定的条件下 A,B是独立的。如假设z=0(常数),则A和B没有任何关联。
等价形式P(A|B,C)=P(A|C)
推导: P(A,B|C)=P(A|C)P(B|C); ...1 P(A,B|C)=P(A|B,C)P(B|C); ...2
联合1,2式可以=> P(A|C)=P(A|B,C)
2.3概率图模型的有向图表示
利用有向图来表示变量之间的概率依赖关系,典型应用就是贝叶斯网络.
上图Naive Bayes 可以表示为: p(y,x1,x2,x3)=p(y).p(x1|y)p(x2|y)p(x3|y)
3. Naive Bayes Model
3.1 Bayes 决策理论思想
朴素贝叶斯是贝叶斯决策理论的一部分, 所以讲述朴素贝叶斯之前有必要快速了解一下贝叶斯决策理论。
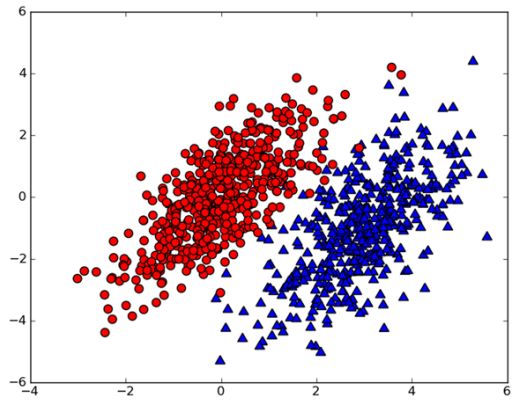
假设我们有一个数据集,如下图所示:
我们用P(c1|x,y) 表示数据点(x,y)属于类别c1的概率(图中红色圆点的概率),用P(c2|x,y)表示数据点(x,y)属于类别c2的概率(图中绿色的三角形概率)。那么对于一个新的数据点(x,y),我们就可以用一下规则来判断它的类别。
- If p(c1|x, y) > p(c2|x, y), then the class is c1.
- If p(c2|x, y) > p(c1|x, y), then the class is c2.
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想, 即选择具有最高概率的决策。
3.2 Naive Bayes 公式推导
假设某个体有n项特征(Feature),分别为F1、F2、...、Fn。现有m个类别(Category),分别为C1、C2、...、Cm。
贝叶斯分类器就是计算出概率最大的那 个 分类,也就是求下面这个算式的最大值:P(C|F1,F2,...,Fn);
可以理解为求 在属性F1,F2,....Fn条件下,属于各个类别Ci的概率,然后求出最大的那个P(Ci|F1,F2,...Fn) ,这样就得到F1,F2,...Fn 属于哪一类(Ci)了。
使用贝叶斯原理可以写成
因为对于每一个类别的Ci的概率都存在P(F1,F2,......Fn)所以只需要关注P(C)P(F1,F2.....Fn|C)
写成联合概率的形式P(C,F1,F2...Fn)=P(C)P(F1,F2.....Fn|C)
重复使用贝叶斯原理=>
现在“朴素”的“条件独立”(2中有推导)假设开始发挥作用:假设每个特征![]() 对于其他特征
对于其他特征![]() ,
,![]() 是条件独立的。这就意味着
是条件独立的。这就意味着
![]()
对于![]() ,所以联合分布模型可以表达为
,所以联合分布模型可以表达为
4. 例子
4.1 性别分类
下面是一组人类身体特征的统计资料。
| 性别 | 身高(英尺) | 体重(磅) | 脚掌(英寸) |
| 男 | 6 | 180 | 12 |
| 男 | 5.92 | 190 | 11 |
| 男 | 5.58 | 170 | 12 |
| 男 | 5.92 | 165 | 10 |
| 女 | 5 | 100 | 6 |
| 女 | 5.5 | 150 | 8 |
| 女 | 5.42 | 130 | 7 |
| 女 | 5.75 | 150 | 9 |
已知某人身高6英尺、体重130磅,脚掌8英寸,请问该人是男是女?
即,P(C|F1,F2,F3)的最大概率。
根据上面的Naive Bayes Model P(C|F1,F2,F3)=P(身高|性别) x P(体重|性别) x P(脚掌|性别) x P(性别)
这里的困难在于,由于身高、体重、脚掌都是连续变量,不能采用离散变量的方法计算概率。而且由于样本太少,所以也无法分成区间计算。怎么办?
这时,可以假设男性和女性的身高、体重、脚掌都是正态分布,通过样本计算出均值和方差,也就是得到正态分布的密度函数。有了密度函数,就可以把值代入, 算出某一点的密度函数的值。
比如,男性的身高是均值5.855、方差0.035的正态分布。所以,男性的身高为6英尺的概率的相对值等于1.5789(大于1并没有关系,因为这里是密度函数的 值,只用来反映各个值的相对可能性)。
如上,我们就可以推出
有了P(height|male),P(weight|male),...我们就可以得到
P(height=6|male) x P(weight=130|male) x P(footsize=8|male) x P(male)
= 6.1984 x e-9
P(height=6|female) x P(weight=130|female) x P(footsize=8|female) x P(female)
= 5.3778 x e-4
可以看到,女性的概率比男性要高出将近10000倍,所以判断该人为女性。
4.2 使用Naive Bayes Model 实现脏话评论
- 分析:
- 训练过程:
已分类[0, 1, 0, 1, 0, 1]
训练评论构成的唯一字典:['maybe', 'him', 'help', 'problems', 'so', 'I', 'dog', 'is', 'cute', 'love', 'buying', 'flea', 'how', 'food', 'licks', 'posting', 'has', 'take', 'stupid', 'steak', 'park', ' please', 'to', 'worthless', 'garbage', 'my', 'dalmation', 'mr', 'quit', 'not', 'ate', 'stop']
训练评论向量化(0表未出现,1表示出现):[[0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0], [1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0], [0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1], [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1], [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0]]
- 分类过程:
__author__ = 'essex.user'
from numpy import *
from math import *
from pylab import *
#load example data
def loadDataSet():
postingList=[['my', 'dog', 'has', 'flea','problems', 'help', 'please'],
['maybe', 'not', 'take', 'him','to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute','I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'my', 'steak', 'how','to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
classVec = [0,1,0,1,0,1] #1 is abusive, 0 not
return postingList,classVec
# create a list of all the unique words in all of our documents
def createVocabList(dataSet):
vocabSet = set([])
for document in dataSet:
vocabSet = vocabSet|set(document)
return list(vocabSet)
#文档的向量(inputSet)是否在词汇表(vacabList)中,则将输出向量的下标变为1
#将文字转化为关于0,1的向量
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else:
print("the word: %s is not in my Vocabulary!" % word)
return returnVec
#朴素贝叶斯分类器训练函数1
def trainNB0(trainMatrix,trainCategory):
#print("trainMatrix:%s\ntrainCategory:%s"%(trainMatrix,trainCategory))
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
#print("numTrainDocs=%d\tnumWords=%d"%(numTrainDocs,numWords))
pAbusive = sum(trainCategory)/float(numTrainDocs) #3/6
p0Num = zeros(numWords); p1Num = zeros(numWords) #长度为32的0向量
#print("pAbusive=%d\np0Num:%s\np1Num:%s"%(pAbusive,p0Num,p1Num))
p0Denom = 0.0; p1Denom = 0.0 #所有文档中,属于类别0和1的词汇个数
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
#print("p1Num:",p1Num)
p1Denom += sum(trainMatrix[i])
#print("p1Denom",p1Denom)
else:
p0Num += trainMatrix[i]
#print("p0Num:",p0Num)
p0Denom += sum(trainMatrix[i])
p1Vect = p1Num/p1Denom #change to log()
p0Vect = p0Num/p0Denom #change to log()
#print("p1Vect:",p1Vect)
return p0Vect,p1Vect,pAbusive
#朴素贝叶斯分类器训练函数--改进版
def trainNB(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix) #文档数
numWords = len(trainMatrix[0]) #词汇表的词汇数
pAbusive = sum(trainCategory)/float(numTrainDocs) #带侮辱性质类别的文档数
p0Num = ones(numWords) #是侮辱性质类别的向量
p1Num = ones(numWords) #长度为32的0向量
p0Denom = 2.0; p1Denom = 2.0 #所有文档中,属于类别0和1的词汇个数
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i] #类别1的词频
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i] #类别0的词频
p0Denom += sum(trainMatrix[i])
p1Vect = log(p1Num/p1Denom)
p0Vect = log(p0Num/p0Denom)
return p0Vect,p1Vect,pAbusive
#朴素贝叶斯分类函数
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
p1 = sum(vec2Classify * p1Vec) + log(pClass1)
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
if p1>p0:
return 1
else:
return 0
#分类器测试
def testingNB():
listOPosts,listClasses = loadDataSet()
myVocabList = createVocabList(listOPosts)
trainMat=[]
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V,p1V,pAb = trainNB(array(trainMat),array(listClasses))
testEntry = ['love', 'my', 'dalmation']
thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))
testEntry = ['stupid', 'garbage']
thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))
testingNB()运行结果:
['love', 'my', 'dalmation'] classified as: 0
['stupid', 'garbage'] classified as: 1