逐步精化的汉诺塔求解（一定能懂、c++实现）

• 本文适用于看了几篇汉诺塔求解答文章，但是还是一知半解的思考者。
• 如果不理解什么是汉诺塔的可以先自行百度。

相信大家对汉诺塔的规则并不陌生。这里不再赘述。
网上关于汉诺塔的代码大同小异，仅仅由于由于我本人偏好C++所以编写如下。

#include
#include
#include
static int step = 0;
using namespace std;
void move(int n, string a, string b)
{
	step++;
	cout <<"第"<> n;
	hanio("一号柱子", "二号柱子", "三号柱子", n);
	return 0;
}

相信这段代码在语法阅读上没有任何的难点。大部分人和我一样，真正的问题是非常不理解，这段代码是怎么来的。

难点在于：这段代码用了一个递归的思路。

在对时间复杂的要求不高，但是空间复杂度要求较大的时。
递归相对于动态规划确实是一个更好的解决方式。
这也是为什么大家都使用这种递归的求解方式来解决汉诺塔问题。

本人在初学递归这个思想的时候，已经陷入了一种迷茫。后来学习了“树”的数据结构之后
通过做题，才开始可以真正地理解递归的思想。

遇到汉诺塔问题的时候，从“前人”代码入手，想当然的想通过画“树”进行求解。事实证明，这样只会让我自己在汉诺塔的问题上更加无所适从。因为代码调用了两次递归。画图非常容易让自己彻底绕进去。显然，在反复的绕晕自己之后，我更加没有信心去理解这段代码本身了。

后来随着学习的加深，对计算机理论的理解。我才可以真正的理解这段代码。

在《计算机网络》这门课程中，我们经常讲“透明”这一概念。简单的说。“透明”就是你进行了一系列的封装，但是我可以直接享受到你封装的成果，而不用管你执行的过程。

透明：在计算机中，客观存在并且运行着但是我们看不到的特性。
客观存在的,但对于某些开发人员而言又不需要了解的东西,这就是计算机所指的透明性.简单来说，透明就是黑盒，你只需要应用它给出的接口，而不需要了解内在机理。

打个最简单的比方，比如我们可以通过3D眼镜看到3D电影，但是我们不需要知道3D眼睛的工作原理一样。此时3D眼镜对我们是透明的。
我认为在汉诺塔问题的求解上，我们也需要在全局上使用透明这一思想。

下面进行汉诺塔求解。这里我用三步来求解这个问题。
首先我定义了一个函数 hanio(x,y,z,n)，他的作用是输入三个柱子的名称，就可以自动的把X上的N个东西通过Y转移到Z柱子上并输出结果。
同时我定义另一个函数move(a,b,n) 其作用是把第N号塔盘从A位置搬到B位置。
（注意我这里的用词，N个和N号，这是非常不一样的）
这俩函数对于我们来说，暂时是透明的。
即：我们可以获得其结果但不需要被其过程约束（即暂时不需要知道原理）。

下面理解第二个概念，首先前提如下：
1、在汉诺塔的规则下，原始柱子的盘子的排列是从1到N然后数字不断变大的过程。
2、大的柱子在小的柱子下方对上方的柱子移动没有影响
那么。我们可以推导如下：如果你的下方有一个数字比你大的盘子，可以认为它是不存在的。
比如你需要把1-3号（1最小，3最大，1在最上方，3在最下方）的盘子移动到第3个柱子。但是游戏出了点Bug,你被分配了1-4号盘子。但是在胜利条件不变的情况下，你的1，2，3号盘子都可以自由自在的移动到一号柱子，你也不需要去动4号盘子，那么这个4号盘子的存在对你原本的移动过程毫无影响，你的胜利条件（最优步数）没有发生任何变化

上文已经提过了：函数 hanio(x,y,z,n)的作用是输入三个柱子的名称，就可以自动的把X上的东西通过Y转移到Z柱子上并输出结果。那么我们如果想在第N个盘子（即最大的最下面的盘子）不参与的情况下，获得游戏的胜利可行吗？

直接一行代码（如下）解决这个问题。

 hanio(x,y,z,n-1)

那么回过头来，如果想让第N个盘子参与这个游戏呢？
那么就先让N-1个盘子到中间的柱子上去，然后把第N个盘子移动到第三个柱子。然后像我之前说的，最大的盘子可以认为是不存在的，所以直接继续把N-1盘子从中间移动到第三个柱子即可。
即：

	hanio( x, z, y, n - 1);
	move(n, x, z);
	hanio(y, x, z, n - 1);

执行这么三行代码就可以实现hanio(x,y,z,n)的效果。
因为他们等价，所以我们可以认为他们就是函数本身。即hanio由上述三行构成如下。

void hanio(string x, string y, string z, int n)
{
	hanio( x, z, y, n - 1);
	move(n, x, z);
	hanio(y, x, z, n - 1);
}

但是思考一下，hanio()中的N有一个逻辑的限制，我们不可以在只有一个盘子（N=1）的情况下，考虑上方N-1个盘子。所以真实场景下，如下的代码才是真正符合逻辑推演的。

void hanio(string x, string y, string z, int n)
{
	if (n == 0)
	{
		return;
	}
	hanio( x, z, y, n - 1);
	move(n, x, z);
	hanio(y, x, z, n - 1);
}

止步于此，我们借助“透明”理解了上述hanio()代码的编写思想。
但是，透明只是一种编程思想。我们最终还是需要了解代码运行的真正逻辑。

来我们继续回顾一下：
目前我们通过前提（如果你的下方有一个数字比你大的盘子，可以认为它是不存在的）：推演出了hanio（x,y,z,n）函数和hanio（x,y,z,n-1）及move（x,y,z）的关系。
但本质上，目前hanio（）对于我们依旧透明。 虽然我们已经看见了其内部的架构。但其架构依赖于move（）和其本身的递归。这一切并不是看见代码就能理解的。

理解其本身的架构之前，我们需要了解一个概念。递归调用栈
解释如下：
0、栈的概念大家应该都知道。如果不知道的请先百度。
1、函数在执行到一半的时候如果调用了别的函数。那么这个函数目前的状况会被压入栈中。然后新的函数的状态会压入同一个栈（在旧的函数上方）等旧的函数执行结束的了。那么旧的函数栈销毁去执行旧的函数。
（例子过于基础，如果有一定的计算机基础的人可以跳过）
举个简单的例子：

#include
using namespace std;
int f2()
{
	return 5;
}
int f1()
{
	return f2() + 3;
}
int main()
{
	cout<

这个代码的执行，是这样执行的。
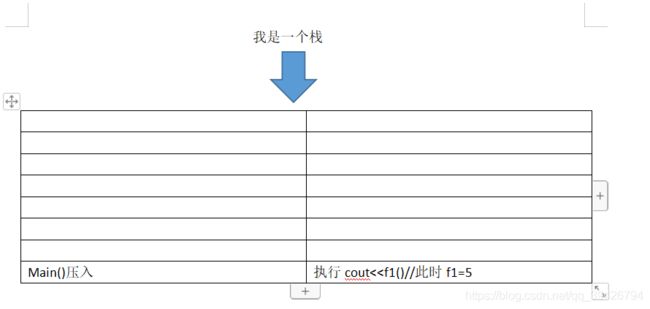
第一步，main()函数执行压入栈，执行到f1()中断

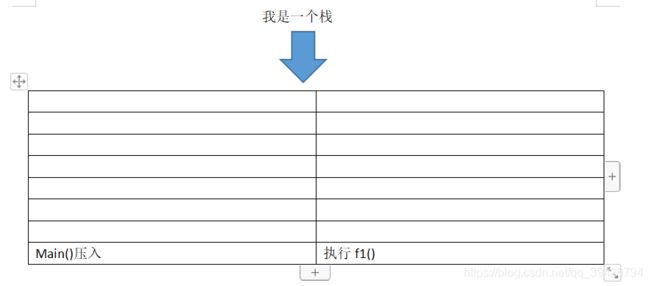
第二步，状态暂存，压入f1()

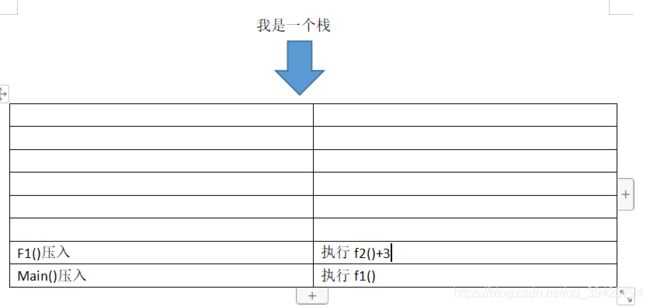
第三步压入f2()

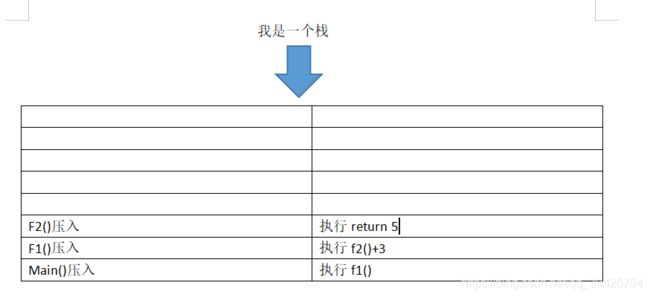
第四步，return 执行，将return的值往栈的新顶部传递，自己销毁

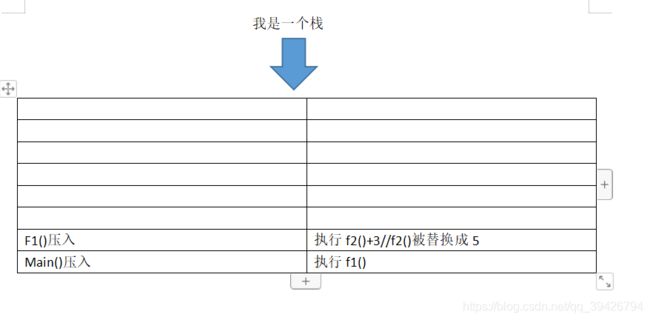
然后第五步的return 类似，f1()层销毁，return的值传给新的栈顶

然后第六步，回到main()函数，从中断处继续执行

最后

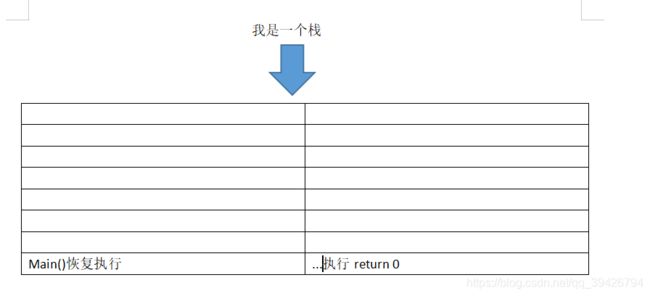
main()层销毁，整个程序执行结束。
（例子结束）

上述是函数间调用真实的栈过程。
而递归本身就是一种特殊的函数间调用，其符合我上述的流程图，只是其不断压入的是其本身，而不是别的函数。本质上没有区别。

不知道大家有没有发现一个特点，如果是这样的话，我们最早调用的代码会在最后才被进行真实的执行。

考虑到递归复杂性。我们仅以N=2进行阐述。
如果我让N=2带入我最早执行的函数那么程序返回的结果是这样的

回到我们上面的代码（如下）

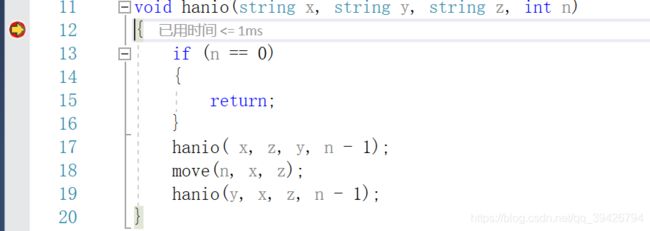
void hanio(string x, string y, string z, int n)
{
	if (n == 0)
	{
		return;
	}
	hanio( x, z, y, n - 1);
	move(n, x, z);
	hanio(y, x, z, n - 1);
}

单步调试
首先进入主函数（第1层栈），调用hanio函数（）
执行到17行(此时第2层栈)

此时各个变量均为输入的值

继续执行，函数进行了一次跳转，原始状态保留，新状态压入栈中。

此时在新栈中：x,y,z如下。

执行执行到17行，又一次跳转到新栈（第3层栈）

此时第3层栈状态如下

进行执行到17行，进入第4层栈
此时
很快由于N=0,这层栈很快的被销毁，我们重新回第3层栈（从中断处开始）

状态保留

我们执行18行，进行第一次移动，把X->Z即把第1号柱子的东西，移动到2号柱子。
然后我们执行第19行，显然N==0所以新的第四层又会被直接销毁。
那么第3层执行结束。回到第2层。
此时的第2层

同样也还在17行的中断处开始

执行到18行，把1号柱子上的东西往3号柱子上移动
执行到19行，状态保留进入新栈（第3层）

新栈中

显然由于N=1第17层创建的新第4层栈会被很快销毁，我们会执行18行的移动，继而
2号柱子移动到3号柱子。
同理19行创建的第4层栈也会被很快销毁。此时，第3层栈执行结束也面临销毁。重新回到第二层栈。
此时的第2层栈，状态恢复如下

第2层栈刚刚恢复，也面临销毁，重新回到第1层栈（主函数）

最后27行执行，栈完全销毁，程序结束。
整个的执行结果如下

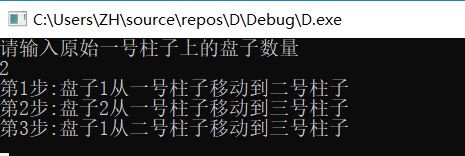
这就是整个汉诺塔的程序运行逻辑。

此文以便日后本人回忆，也希望给大家带来帮助。