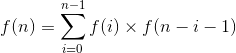ACM组合数学模板
排列：
不可重复排列：
可重复排列：从n个取可重复k个排列数为：
圆排列：
错位排列：![D_n=n!(\frac{1}{2!}-\frac{1}{3!}+...+(-1)^n\frac{1}{n!})=[\frac{n!}{e}+0.5]](http://img.e-com-net.com/image/info8/b112a7e8745d430da902849cf27b0103.gif){kind=small}
指数母函数定义：
组合：
不可重复组合：
可重复组合：
不相邻组合：从n个取m个不相邻组合数为：
组合常用公式：
帕斯卡恒等式：
普通母函数定义：
常见数列：
斐波那契数列：
![a_{n} = \frac{1 }{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}]](http://img.e-com-net.com/image/info8/fd747efc5c154ee38bec533955cfb341.gif){kind=small}
卡特兰数列：
递归公式1：
递归公式2：
组合公式1：
组合公式2：
全排列
/*==================================================*\
| perm1: 由于与perm3完成的功能差不多，建议使用perm3
| perm2: 可从N个取M的全排列
\*==================================================*/
#include
using namespace std;
const int N = 10;
int array[] = {1,2,3,4,5,6,7,8,9,10};
const int M = 3; // 从N位数选择M个全排列
int results[M]; // 结果集
int cnt = 0;
bool is_used[N];
void perm1(int deep) {
// 递归结束，打印
if(deep == N) { cnt++; return ; }
// 递归遍历
for(int i=deep; i < N; i++) {
{int temp = array[i]; array[i]=array[deep]; array[deep]=temp;}
perm1(deep+1);
{int temp = array[i]; array[i]=array[deep]; array[deep]=temp;}
}
}
void perm2(int deep) {
// 递归结束，打印
if (deep == M) { cnt++; return ; }
// 递归遍历
for (int i = 0; i < N; i++) {
if (!is_used[i]) {
is_used[i] = true;
results[deep] = array[i];
perm2(deep+1);
is_used[i] = false;
}
}
}
int main() {
perm1(0);
perm2(0);
do {
cnt++;
} while(next_permutation(array,array+N));
cout << cnt << endl;
return 0;
} 组合
/*==================================================*\
| comb1: C(n, m) n=29，m=15花费时间较多 1ms
| comb2: C(n, m) n=27，m=27花费时间较多 1ms
\*==================================================*/
#include
using namespace std;
// 数组的长度
const int N = 3;
// 初始化数组
int array[N] = {1,2,3};
// 组合数个数
const int M = 2;
// 结果集
int results[M];
// 当comb_end == n时结束递归
int comb_end = 0;
// 结果数量
int cnt = 0;
void comb1(int deep, int m){
if ( !m ) { cnt++; return ; }
for (int i=deep; i <= N-m; i++){
results[comb_end++] = array[i];
comb1(i+1, m-1);
comb_end--;
}
}
void comb2(int deep) {
// 越界递归结束
if(deep > N) return ;
// 递归结束，打印
if(comb_end == M) { cnt++; return ; }
// 递归遍历
results[comb_end++] = array[deep];
comb2(deep+1);
comb_end--;
comb2(deep+1);
}
int main() {
comb1(0, M);
comb2(0);
cout << cnt<< endl;
return 0;
} 组合数
/*==================================================*\
| 组合数C(n, r)
\*==================================================*/
ll com(int n, int r){// return C(n, r)
if(r > n-r) r = n-r; // C(n, r) = C(n, n-r)
ll u = 1, d = 1;
for(int i=0; i < r; ++i ) {
u *= (n - i);
d *= (r - i);
}
return u / d;
}
/*==================================================*\
| O(n) 求组合数 从开始从左到右递推,注意爆int
| C(n,i) = c(n,i-1) * n-i+1 / i
\*==================================================*/
C[0] = 1;
for(int i = 1; i <= n; i++)
C[i] = C[i - 1] * (n - i + 1) / i;
组合数取模
/*==================================================*\
| 组合数C(n, r) % mod
\*==================================================*/
//const LL maxn(1000005), mod(1e9 + 7);
ll fac[maxn]; // 阶乘
void init() {
fac[0] = fac[1] = 1;
for(ll i = 2; i < maxn; i++)
fac[i] = fac[i - 1] * i % mod;
}
ll getInv(int b) {
if(b == 1) return 1;
return (mod-mod/b) * getInv(mod%b) % mod;
}
LL C(LL a, LL b) {
return fac[a] * getInv(fac[b]) % mod * getInv(fac[a - b]) % mod;
}卡特兰数列
/*--------------------------------------------------
卡特兰数列：1, 2, 5, 14, 42, 132, 429, 1430...
常见用法：
卡特兰数的应用都可以归结到一种情况：有两种操作，
分别为操作一和操作二，它们的操作次数相同，
都为 N，且在进行第 K 次操作二前必须先进行至少 K 次操作一，
问有多少中情况？结果就Catalan(N)。
1.给定n个数，有多少种出栈序列
2.n个结点的二叉树有多少种构型
3.在nn的格子中，只在下三角行走，每次横或竖走一格，有多少种走法
4.将一个凸n+2边型剖分成三角形的方法数
5.在圆上选择2n个点，将这些点成对相连使得到的n条线段不相交的方法数
6.n个长方形填充一个高度为n的阶梯状图形的方法数
7.括号化问题，左括号和右括号各有n个时，合法的括号表达式的种类
8.有n+1个数连乘，乘法顺序的种类
9.n位二进制中，有m个0，其余为1，有h[C(n,m)-C(n,m-1)]种
--------------------------------------------------*/
void catalan() { // 递归公式1 （n < 36）
h[0] = h[1] = 1;
for(int i=2; i < 36; i++) {
h[i] = 0;
for(int j=0; j < i; j++)
h[i] += h[j] * h[i-j-1];
}
}
ll catalan(ll n) { // n >= 36， C位组合数
return (C(2*n,n) - C(2*n,n-1) + mod) % mod;
}
整数拆分
/*==================================================*\
| 有序拆分：把自然数n拆分成r个自然数之和，方案数有C(n-1,r-1)
| 无序拆分：把自然数n拆分成m个自然数之和
| 方案数有F(n,m)=F(n-1,m-1)+F(n-m,m),F(n,1)=F(n,n)=1
\*==================================================*/
ll solve(int n, int m) {
return C(n-1, m-1);
}
ll F(int n, int m) {
if(m == 1 || n == m) return 1;
if(n < m) return 0;
return F(n-1,m-1) + F(n-m,m);
}
/*==================================================*\
| 无序拆分：把自然数n拆分成不多于m个自然数之和
| 方案数有F(n,m)=F(n-1,m-1)+F(n-m,m),F(n,1)=F(n,n)=1
\*==================================================*/
ll F(int n, int m) {
if(m == 1) return 1;
if(n < m) return F(n, n);
if(n == m) return F(n, m-1) + 1;
return F(n-m,m) + F(n,m-1);
}错排问题
/*------------------------------------------------------------
问题： 十本不同的书放在书架上。
现重新摆放，使每本书都不在原来放的位置。有几种摆法？
这个问题推广一下，就是错排问题，是组合数学中的问题之一。
考虑一个有n个元素的排列，若一个排列中所有的元素都不在自己原来的位置上，
那么这样的排列就称为原排列的一个错排。 n个元素的错排数记为D(n)。
研究一个排列错排个数的问题，叫做错排问题或称为更列问题。
------------------------------------------------------------*/
// dp[1]=0, dp[2]=1
// dp[i] = (i - 1)*(dp[i - 1] + dp[i - 2]); i > 2
ll D(int n) {
ll a = 0, b = 1, c;
if(n < 3) return n-1;
for (int i = 3; i <= n; i++) {
c = ((i - 1) * 1ll * (a + b)) % mod;
a = b;
b = c;
}
return c;
}
普通母函数
/*--------------------------------------------------
经典例题：有质量为1、2、4的砝码分别为1、3、2枚
问：可以称出多少不同质量？要称出质量为3有几种方式？
解：构造函数G(x)=(1+x)*(1+x^2+x^4+x^6)*(1+x^4+x^8)
其中第二个括号中X^6表示：用第二个物品质量3枚,以此类推
代码为模拟构造函数计算过程 比如：
(1+x) * (1+x^2+x^4+x^6) * (1+x^4+x^8)
= (1+x^2+x^4+x^6 + x+x^3+x^5+x^7) * (1+x^4+x^8)
= ...
代码理解：将括号中的项与前面已经算过的项相乘
由于第一个没前项，所有乘个1，即a[0] = 1
j*v[i]即第i个括号中第j项的系数，
k+j*v[i]即j*v[i]系数项乘k系数项
--------------------------------------------------*/
// 物品的个数
const int n = 3;
// 所有物品相加出现的最大指数
const int P = 15;
// v[i]第i个未知量价值，s/e:物品的最少/最多个数
int v[n]={1,2,4}, s[n]={0,0,0}, e[n]={1,3,2};
// a为最终结果，b为中间结果。
int a[P+1], b[P+1];
// P为可能出现的最大指数
void init() {
memset(a, 0, sizeof(a));
memset(b, 0, sizeof(b));
a[0] = 1; // 1 * G(x)
for(int i=0; i < n; i++) {
for (int j=s[i]; j<=e[i] && j*v[i]<=P; j++) {
for (int k=0; k+j*v[i] <= P; k++)
b[k+j*v[i]] += a[k];
}
memcpy(a, b, sizeof(b));
memset(b, 0, sizeof(b));
}
// return a[3] // 称出质量为3有几种方式？
// return sum(a[i]!=0) // 可以称出多少不同质量？
}指数母函数
/*--------------------------------------------------
经典例题：假设有多个元素，其中a1重复n1次，a2重复n2次，
a3重复n3次。从中取r个排列，求其排列数。
构造函数G(x) = (1+x/1!+x^2/2!+...+x^n1/n1!) *
(1+x/1!+...+x^n2/n2!) *(1+x/1!+...+x^n3/n3!)
算法理解：用前面算好的乘后面要算的数（与普通母函数相反）
j为前项的指数 k为当前项指数 k+j 为相乘后的指数
--------------------------------------------------*/
const int m = 3; // 取m个
int a[] = {1,2,3}; // 每种数的个数
ll fac[m + 1]; // 阶乘
double c1[m+1], c2[m+1]; // double
void cal(int n,int m) { //有n种，取m个
memset(c1, 0, sizeof(c1));
memset(c2, 0, sizeof(c2));
c1[0] = 1.0 / fac[0]; // 1 * G(x)
for(int i=0; i < n; i++) {
for(int j=0; j <= m; j++) {
for(int k=0; k+j<=m && k<=a[i]; k++)
c2[k+j] += c1[j] / fac[k];
}
for(int j=0; j <= m; j++) {
c1[j] = c2[j];
c2[j] = 0;
}
}
// return c1[m] * fac[m]; //取m个时的多重排列数
}莫比乌斯函数
// 递推筛法 n*logn
void getMu(){
for(int i=1; i<=MAXN; i++) {
int target = i==1?1:0;
int delta = target - mu[i];
mu[i]=delta;
for(int j=i*2; j<=MAXN; j+=i)
mu[j]+=delta;
}
}
//线性筛法求莫比乌斯函数
bool check[MAXN+10];
int prime[MAXN+10];
int mu[MAXN+10];
void Moblus() {
memset(check,false,sizeof(check));
mu[1] = 1;
int tot = 0;
for(int i = 2; i <= MAXN; i++) {
if( !check[i] ) {
prime[tot++] = i;
mu[i] = -1;
}
for(int j = 0; j < tot; j++) {
if(i * prime[j] > MAXN) break;
check[i * prime[j]] = true;
if( i % prime[j] == 0){
mu[i * prime[j]] = 0;
break;
}else{
mu[i * prime[j]] = -mu[i];
}
}
}
}
// 求sum(d)=∑p|dμ(dp)
const int maxn = 10000010;
int prime[maxn],mu[maxn],sum[maxn];
bool check[maxn];
void Mobius(){
memset(check,false,sizeof(check));
mu[1] = 1;
prime[0] = 0;
for(int i=2;i= maxn) break;
check[i*prime[j]] = true;
if(i % prime[j]){
mu[i*prime[j]] = -mu[i];
sum[i*prime[j]] = mu[i] - sum[i];
}
else{
mu[i*prime[j]] = 0;
sum[i*prime[j]] = mu[i];
break;
}
}
}
}
Polya计算
/*==================================================*\
| c种颜色的珠子, 组成长为s的项链, 项链没有方向和起始位置;
\*==================================================*/
int gcd (int a, int b) { return b ? gcd(b,a%b) : a; }
int main (void){
int c, s;
while (scanf("%d%d", &c, &s)==2) {
int k;
long long p[64]; p[0] = 1; // power of c
for (k=0 ; k代码多源于网络，更多模板