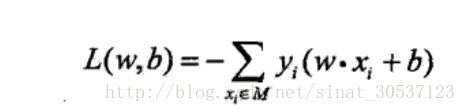【用python实现《统计学习方法》】之感知机(perceptron)
声明:首先非常感谢李航博士和这篇博文的博主。本文的理论部分主要参考李航博士的《统计学习方法》,而代码实现部分则是在上述的博文基础上完成,并新增了对偶形式的感知机的python实现。
感知机(perceptron)是机器学习中最简单的算法之一,容易理解和实现。笔者将使用python实现感知机的算法(重复造轮子),包括感知机的原始形式和对偶形式。
model
感知机的定义:
strategy
感知机学习的经验风险函数:
algorithm
原始形式的感知机算法:
算法的python实现:
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
class Perceptron(object):
"""
原始形态感知机
"""
def __init__(self, eta=0.01, n_iter=10):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
"""
拟合函数,使用训练集来拟合模型
:param X:training sets
:param y:training labels
:return:self
"""
# X's each col represent a feature
# initialization wb(weight plus bias)
self.wb = np.zeros(1 + X.shape[1])
# the main process of fitting
self.errors_ = [] # store the errors for each iteration
for _ in range(self.n_iter):
errors = 0
for xi, yi in zip(X, y):
update = self.eta * (yi - self.predict(xi))
self.wb[1:] += update * xi
self.wb[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def net_input(self, xi):
"""
计算净输入
:param xi:
:return:净输入
"""
return np.dot(xi, self.wb[1:]) + self.wb[0]
def predict(self, xi):
"""
计算预测值
:param xi:
:return:-1 or 1
"""
return np.where(self.net_input(xi) <= 0.0, -1, 1)对偶形式的感知机算法:
算法的python实现:
a, b, G_matrix = 0, 0, 0
# 计算Gram Matrix
def calculate_g_matrix(data):
global G_matrix
G_matrix = np.zeros((data.shape[0], data.shape[0]))
# 填充Gram Matrix
for i in range(data.shape[0]):
for j in range(data.shape[0]):
G_matrix[i][j] = np.sum(data[i, 0:-1] * data[j, 0:-1])
# 迭代的判定条件
def judge(data, y, index):
global a, b
tmp = 0
for m in range(data.shape[0]):
tmp += a[m] * data[m, -1] * G_matrix[index][m]
return (tmp + b) * y
def dual_perceptron(data):
"""
对偶形态的感知机
由于对偶形式中训练实例仅以内积的形式出现
因此,若事先求出Gram Matrix,能大大减少计算量
:param data:训练数据集;ndarray object
:return:w,b
"""
global a, b, G_matrix
# 计算Gram_Matrix
calculate_g_matrix(data)
# 读取数据集中含有的样本数
num_samples = data.shape[0]
# 读取数据集中特征向量的个数
num_features = data.shape[1] - 1
# 初始化a,b
a, b = [0] * num_samples, 0
# 初始化weight
w = np.zeros((1, num_features))
i = 0
while i < num_samples:
if judge(data, data[i, -1], i) <= 0:
a[i] += 1
b += data[i, -1]
i = 0
else:
i += 1
for j in range(num_samples):
w += a[j] * data[j, 0:-1] * data[j, -1]
return w, b算法实现后需要进行测试,我们先从sklearn.datasets里面获取一个线性可分的数据集iris,并进行交叉验证切割,将数据集分为training set 和test set,最后使用training set 对我们实现的感知机模型进行拟合,代码如下:
def main():
iris = load_iris()
X = iris.data[:100, [0, 2]]
y = iris.target[:100]
y = np.where(y == 1, 1, -1)
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.3)
ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X_train, y_train) 然后我们在Perceptron类里面实现一个可视化方法,方法代码如下:
def plot_decision_regions(self, X, y, resolution=0.02):
"""
拟合效果可视化
:param X:training sets
:param y:training labels
:param resolution:分辨率
:return:None
"""
# initialization colors map
colors = ['red', 'blue']
markers = ['o', 'x']
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision regions
x1_max, x1_min = max(X[:, 0]) + 1, min(X[:, 0]) - 1
x2_max, x2_min = max(X[:, 1]) + 1, min(X[:, 1]) - 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = self.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# plot class samples
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=cmap(idx),
marker=markers[idx], label=cl)
plt.show()然后用test set 测试拟合效果:
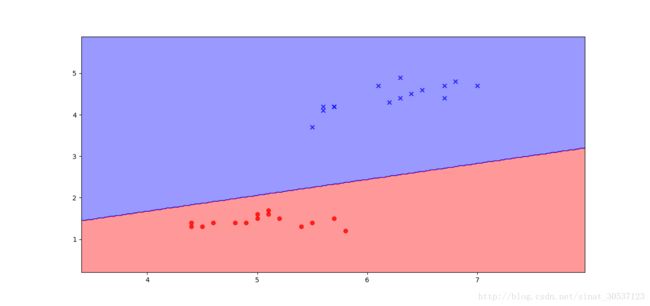
ppn.plot_decision_regions(X_test, y_test)效果图如下,可以发现,我们成功的预测出一个模型,能很好的对iris数据集进行分类。
最后,测试一下程序是否正确执行并生成了weight、bias。