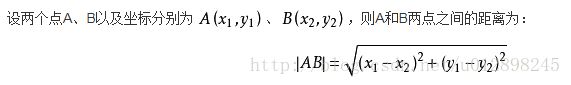JAVA判断一个地理坐标是否在一个多边形区域内和是否在一个圆形区域内(经纬度)
怎么样判断一个坐标点在一个多边形区域内?包括规则多边形,不规则多边形,还有圆。。。
1 判断一个坐标是否在圆形区域内?
多边形和圆分开写,首先简单的就是判断是否在圆里面,如何判断一个坐标是否在圆形区域内,相信不用我说都知道,计算这个坐标点和圆心之间的距离,然后跟圆的半径进行比较,如果比半径大,就不在圆形区域内,如果小于等于圆的半径,则该坐标点在圆形区域内。
数学上的计算公式是这样的:
代码采用谷歌地图计算距离的方式,应该算是比较精确。
private static double EARTH_RADIUS = 6378.137;
private static double rad(double d) {
return d * Math.PI / 180.0;
}
/**
* 通过经纬度获取距离(单位:米)
*
* @param lat1
* @param lng1
* @param lat2
* @param lng2
* @return
*/
public static double getDistance(double lat1, double lng1, double lat2,
double lng2) {
double radLat1 = rad(lat1);
double radLat2 = rad(lat2);
double a = radLat1 - radLat2;
double b = rad(lng1) - rad(lng2);
double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) +
Math.cos(radLat1) * Math.cos(radLat2) * Math.pow(Math.sin(b / 2), 2)));
s = s * EARTH_RADIUS;
s = Math.round(s * 10000d) / 10000d;
return s;
}
/**
* 判断一个点是否在圆形区域内
*/
public static boolean isInCircle(double lng1, double lat1, double lng2, double lat2, String radius) {
return getDistance(lat1, lng1, lat2, lng2) > Double.parseDouble(radius);
}(如果使用Math.hypot()方法,计算(经纬度距离时)结果会有偏差):
double x = (lon1 - lon2) * PI * R * Math.cos(((lat1 + lat2) / 2) * PI / 180) / 180;
double y = (lat1 - lat2) * PI * R / 180;
double distance = Math.hypot(x, y);
2 判断一点是否在一个多边形区域内?
这里用到JAVA的关于坐标系和几何图形的一个类GeneralPath,使用这个类,结合传入的各顶点参数,画一个几何图形,并通过它自身的contains方法,判断一点是否在这个几何图形内。
也就是,通过JAVA已经封装好的方法,画一个几何多边形,判断一点是否在这个几何多边形里面。
代码里面也有注释:
/**
* 判断是否在多边形区域内
*
* @param pointLon
* 要判断的点的纵坐标
* @param pointLat
* 要判断的点的横坐标
* @param lon
* 区域各顶点的纵坐标数组
* @param lat
* 区域各顶点的横坐标数组
* @return
*/
public static boolean isInPolygon(double pointLon, double pointLat, double[] lon,
double[] lat) {
// 将要判断的横纵坐标组成一个点
Point2D.Double point = new Point2D.Double(pointLon, pointLat);
// 将区域各顶点的横纵坐标放到一个点集合里面
List pointList = new ArrayList();
double polygonPoint_x = 0.0, polygonPoint_y = 0.0;
for (int i = 0; i < lon.length; i++) {
polygonPoint_x = lon[i];
polygonPoint_y = lat[i];
Point2D.Double polygonPoint = new Point2D.Double(polygonPoint_x, polygonPoint_y);
pointList.add(polygonPoint);
}
return check(point, pointList);
}
/**
* 一个点是否在多边形内
*
* @param point
* 要判断的点的横纵坐标
* @param polygon
* 组成的顶点坐标集合
* @return
*/
private static boolean check(Point2D.Double point, List polygon) {
java.awt.geom.GeneralPath peneralPath = new java.awt.geom.GeneralPath();
Point2D.Double first = polygon.get(0);
// 通过移动到指定坐标(以双精度指定),将一个点添加到路径中
peneralPath.moveTo(first.x, first.y);
polygon.remove(0);
for (Point2D.Double d : polygon) {
// 通过绘制一条从当前坐标到新指定坐标(以双精度指定)的直线,将一个点添加到路径中。
peneralPath.lineTo(d.x, d.y);
}
// 将几何多边形封闭
peneralPath.lineTo(first.x, first.y);
peneralPath.closePath();
// 测试指定的 Point2D 是否在 Shape 的边界内。
return peneralPath.contains(point);
} 有没有感觉很方便很简单。。。
以上是用到的各方法介绍。。。
3 当然解决问题的方法肯定不止一种。这里还有一种比较简单的判断一点是否在一个多边形区域内的方法
先将横纵坐标数组的横坐标最大最小值,纵坐标的最大最小值,求出来,需要判断的一点大于横纵坐标的最大值或者小于横纵坐标的最小值,也就是粗略的计算一下,如果这个条件不满足的话,就不用往下计算了,直接不在指定的区域里面。
也就是:
/**
* 判断该地理坐标是否在最大范围区域内
*
* @param pointLon
* 要判断的点的纵坐标
* @param pointLat
* 要判断的点的横坐标
* @param lon
* 指定区域的纵坐标组成的数组
* @param lat
* 指定区域的横坐标组成的数组
* @return
*/
private static boolean isInMaxArea(double pointLon, double pointLat, double[] lon,
double[] lat) {
// 获取区域横纵坐标最大值和最小值
double temp = 0.0;
for (int i = 0; i < lon.length; i++) {
for (int j = 0; j < lon.length - i - 1; j++) {
if (lon[j] > lon[j + 1]) {
temp = lon[j];
lon[j] = lon[j + 1];
lon[j + 1] = temp;
}
}
}
for (int i = 0; i < lat.length; i++) {
for (int j = 0; j < lat.length - i - 1; j++) {
if (lat[j] > lat[j + 1]) {
temp = lat[j];
lat[j] = lat[j + 1];
lat[j + 1] = temp;
}
}
}
// 如果在最值组成的区域外,那肯定不在重点区域内
return (pointLon < lon[0] || pointLon > lon[lon.length - 1] || pointLat < lat[0]
|| pointLat > lat[lat.length - 1]);
}如果通过了上面的判断,可以进行接下来的算法判断了
用到了两点间的斜率公式
这个方法就是,通过一点,画一条线,这条线与多边形相交,如果相交点数位奇数,就在区域内,如果为偶数,就不在区域内
代码:
/**
* 判断坐标是否在重点区域内
*
* @param pointLon
* 要判断的点的纵坐标
* @param pointLat
* 要判断的点的横坐标
* @param lon
* 指定区域的纵坐标组成的数组
* @param lat
* 指定区域的横坐标组成的数组
* @return
*/
private static boolean isInAccurateArea(double pointLon, double pointLat, double[] lon,
double[] lat) {
// 代表有几个点
int vertexNum = lon.length;
boolean result = false;
for (int i = 0, j = vertexNum - 1; i < vertexNum; j = i++) {
// 满足条件,与多边形相交一次,result布尔值取反一次,奇数个则在区域内
if ((lon[i] > pointLon) != (lon[j] > pointLon)
&& (pointLat < (lat[j] - lat[i]) * (pointLon - lon[i]) / (lon[j] - lon[i])
+ lat[i])) {
result = !result;
}
}
return result;
}好了,就这些了,哪里不对欢迎指教。。。有问题也可以探讨。