数论，组合数学相关

内容

1. 同余定理的应用
2. gcd
3. 快速幂
4. 快速乘

 

同余定理的应用

最简单的应用：

(a+b)%p == (a%p + b%p) % p

(a-b)%p == (a%p - b%p) % p

a*b%p == ( (a%p)*(b%p) ) % p

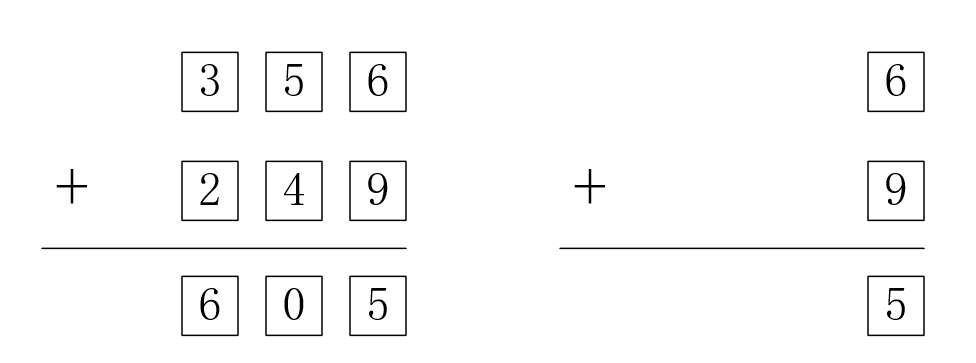
 其实就是加减乘的运算都可以边运算边取模，这和运算结果出来后再取模是一样的。比如：(a+b*c-d)%p == (a%p + b%p*c%p - d%p) % p 。目的：防止结果太大，爆类型。理解：用竖式计算理解：

当计算(356+249)%10的时候，我们只需要看个位数相加（6+9），然后再模10就行了。对于(a+b)%p，这里的“个位数”相当于"a%p"，"b%p"。对于减法和乘法同理可得。但是除法是不能边除边模的。为什么？因为除法的竖式计算和加减乘法的竖式计算不一样啊（扯淡说法(￣▽￣)"，便于理解记忆而已）。

gcd

gcd：greatest common divisor，最大公约数。其中有关gcd最出名的就是欧几里得算法，也就是辗转相除法。刚开始我直接记公式：gcd(a, b) = gcd(b, a%b)，却没有理解里面的内涵，然后就卡了师兄说很简单的一道题?，后面仔细推导了一下，就瞬间明白了。

推导：我们假设a >= b，则gcd(a, b) = gcd(b, a)，接下来要推导gcd(b, a) == gcd(b, a%b)：

证明：gcd(b, a) == gcd(b, a%b)

（下面k1-k5都是整数）

记c = a % b，则：b = k1*gcd(b, c)，c  = k2*gcd(b, c)

a = k3*b + c

   = k3*k1*gcd(b, c) + k2*gcd(b, c) = gcd(b, c) * (k3*k1+k2)

即gcd(b, c)是a的因子，即gcd(b, a%b)是a的因子（约数）。

 

接下来用反证法证明gcd(b, a%b)是b和a的“最大”的公约数：

假设gcd(b, a%b)不是b和a的“最大”的公约数，即gcd(b, c)不是b和a的“最大”公约数，则：

gcd(b, a)是b的因子，而不是c的因子（如果gcd(b, a)是c的因子，那么通过gcd(b, c)就可以求出gcd(b, a)  (c <= a) ）。

由：a = k3*b + c ⇔ k4*gcd(b, a) = k3*k5*gcd(b, a) + c ⇔ c = gcd(b, a) * (k4-k3*k5)，即gcd(b, a)是c的因子，与上述矛盾。

故gcd(b, a) == gcd(b, a%b)

这个结论的推论就是：gcd(b, a)  == gcd(b, a-k*b)（其中k为整数），这个推论也可以由上易证。

快速幂

快速幂其实就是“翻倍”相乘，比如，要算5^15，我们可以这样拆开：5^( 1 + 2 + 4 + 8 )，变成 (5^1) * (5^2) * (5^4) * (5^8)。计算5^2时，就是把5^1“翻倍”，也就是算(5^1)^2；计算5^4时，就是把5^2"翻倍"，也就是算(5^2)^2；计算5^8时同理可得。所以，代码就是：

int base = 5;
int res = 1;
for(int i = 1; i <= 4; i++){
    res = res * base;
    base = base * base;
}

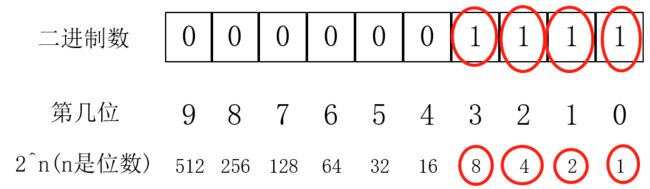
但是，如果幂没有这么特殊，假如算5^10，那这个怎么办？我们回过头来看5^15这个例子，我们看到：1，2，4，8 ----- 这些数都是2的幂次（当然是2的幂次啦，不是2的幂次怎么“翻倍”）。显然，这些数加起来是15（ 废话(￣▽￣)" ）。那么，我们怎样选，才能选出一组是2的幂次的数（这里就是1,2,4,8），而且加起来是等于幂（这里的幂就是15）。答案就在于二进制。我们把15转化成二进制就是：

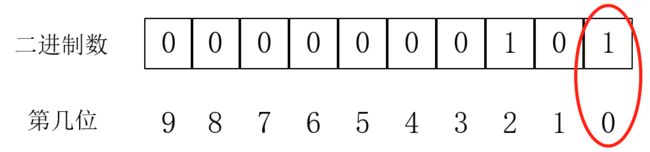
其实就是15 == 1*(2^0) + 1*(2^1) + 1*(2^2) + 1*(2^3) == 1*1+1*2+1*4+1*8。同理，对于5^10的幂（就是10），我们转化为二进制后，就是这样：

其实就是10 == 0*(2^0) + 1*(2^1) + 0*(2^2) + 1*(2^3) == 0*1+1*2+0*4+1*8。对比：

15 = 1 + 2 + 4 + 8

10 =       2 +       8

或者：

15 = 1 * 1  +  1 * 2  +  1 * 4  +  1 * 8

10 = 0 * 1  +  1 * 2  +  0 * 4  +  1 * 8

二进制帮助了我们对于2的幂次的数（也可以称为公比为2，首项为1的等比数列，其实也就是1,2,4,8,16,32.......）的选择：选（对应的二进制数位为1）和不选（对应的二进制数位为0）。对于15，就是这个样子的：1,2,4,8都选，对于10，只选2,8，不选1,4。这样弄有什么好处呢？我们直接来看代码：

1 //快速幂模板
2 int base = 5;  //base:底数
3 int m = 10;    //m:幂
4 int res = 1    //res:结果
5 while(m){
6     if(m % 2 == 1) res = res * base;  
7     base = base * base;    
8     m = m / 2;
9 }

首先，我们看看第7行代码：其实就是翻倍，得到base^1，base^2，base^4，base^8......。对于第6行的代码，我想有人大概猜到了是什么作用：如果当前二进制位是1，那么就乘上base，否则不乘入结果。对应我们的5^10来说，就是res = (base^2)*(base^8)（上面提到了对于10只选2,8）。那么，我们怎样取出10的二进制位？对于二进制的位是0时，只要判断数的奇偶，就可以判断0位的二进制是0还是1：

对于二进制的位是1的时候：

我们只需要把二进制数向右移一位，也就是这样：

这时，之前二进制的1位变成了二进制的0位。我们只需要按照之前的方法就可以判断这个位到底选不选。右移一位的操作：第8行代码，就是直接除2。呃，解释的话，就是向右移一位时，因为所有的位都要向右一位，而一位的大小是2，所以要除于2，这跟把一个十进制的数里面的每个位取出来的道理是一样的。经过更形象的修改，我们还可以把代码改成这样：

1 //快速幂模板
2 int base = 5;  //base:底数
3 int m = 10;    //m:幂
4 int res = 1    //res:结果
5 while(m){
6     if(m & 1) res *= base;  
7     base *= base;    
8     m >>= 1;
9 }

 

如何判断幂的二进制位全部取出来？当幂被右移变成0时就说明没有位可取了，就是第5行代码。

不懂的话可以直接复制以上模板。

快速乘

其实快速乘一点也不“快速”。快速乘会应用到这种情形：要计算a*b%p，发现a*b爆long long了，而我们的a, b, p是没有爆long long的。如果我们手写高精度算法会显得很麻烦，这时就要用到快速乘。快速乘和快速幂的原理是差不多的。比如要计算5*15，那么，我们可以这样拆：5*( 1 + 2 + 4 + 8 )，然后用去括号，就得出 5*1+5*2+5*4+5*8，接下来推导过程和快速幂一样，就是base^2改成base*2，”翻倍"方式不同而已。当我们计算的时候，只需要边乘边取模就行了。代码：

 1 //快速乘模板
 2 int mod = p;
 3 int base = 5;
 4 int m = 15;
 5 int res = 0;
 6 while(m){
 7     if(m & 1) res = (res+base)%mod;
 8     base = (base+base)%mod;
 9     m >>= 1;
10 }

 

暂更

 

转载于:https://www.cnblogs.com/happy-MEdge/p/10503565.html