Matlab 图论最短路问题模型代码

最短路问题的基本内容

最短路问题研究的是，在一个点与点之间连接形成的网络图中，对应路径赋予一定的权重(可以理解为两点之间的距离)，计算任意两点之间如何和走，路径最短的问题。在这里的距离可以理解成各种两点之间某种任务的开销。

网络图

模型调用

解决最短路问题，一般可采取 dijkstra 或者floyd 这两种模型，模型调用形式如下：

[mydist,mypath]=mydijkstra(a,sb,db) % dijkstra模型
[mydist,mypath]=myfloyd(a,sb,db) % floyd模型

其中，

• a 为邻接矩阵
• sb 为起点标号
• db 为终点标号
• mydist 为最短路径长度
• mypath 为最短路径

模型完整代码

Dijkstra 模型代码

function [mydistance,mypath]=mydijkstra(a,sb,db);
% 输入：a—邻接矩阵，a（i，j)是指i到j之间的距离，可以是有向的
% sb—起点的标号, db—终点的标号
% 输出：mydistance—最短路的距离, mypath—最短路的路径
n=size(a,1); visited(1:n) = 0;
distance(1:n) = inf; distance(sb) = 0; %起点到各顶点距离的初始化
visited(sb)=1; u=sb;  %u为最新的P标号顶点
parent(1:n) = 0; %前驱顶点的初始化
for i = 1: n-1
     id=find(visited==0); %查找未标号的顶点
     for v = id           
         if  a(u, v) + distance(u) < distance(v)
             distance(v) = distance(u) + a(u, v);  %修改标号值 
             parent(v) = u;                                    
         end            
     end
     temp=distance;
     temp(visited==1)=inf;  %已标号点的距离换成无穷
     [t, u] = min(temp);  %找标号值最小的顶点 
     visited(u) = 1;       %标记已经标号的顶点
 end
mypath = [];
if parent(db) ~= 0   %如果存在路!
    t = db; mypath = [db];
    while t ~= sb
        p = parent(t);
        mypath = [p mypath];
        t = p;      
    end
end
mydistance = distance(db);

Floyd 模型代码

function [dist,mypath]=myfloyd(a,sb,db);
% 输入：a—邻接矩阵，元素(aij)是顶点i到j之间的直达距离，可以是有向的
% sb—起点的标号；db—终点的标号
% 输出：dist—最短路的距离；% mypath—最短路的路径
n=size(a,1); path=zeros(n);
for k=1:n
    for i=1:n
        for j=1:n
            if a(i,j)>a(i,k)+a(k,j)
                a(i,j)=a(i,k)+a(k,j);
                path(i,j)=k;
            end
        end
    end
end
dist=a(sb,db);
parent=path(sb,:); %从起点sb到终点db的最短路上各顶点的前驱顶点
parent(parent==0)=sb; %path中的分量为0，表示该顶点的前驱是起点
mypath=db; t=db;
while t~=sb
        p=parent(t); mypath=[p,mypath];
        t=p;
end

案例演示

对于上面的网络图，求解从 A 到 D 的最短路径。

整理邻接矩阵

首先整理出点与点之间连接关系，得出邻接矩阵。

假设点的排序为：

点位	A	B1	B2	C1	C2	C3	D
序号	1	2	3	4	5	6	7

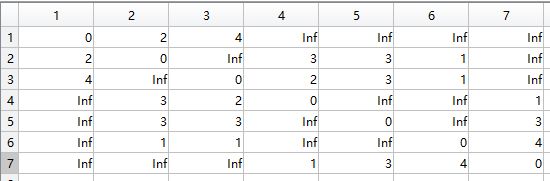
整理出 7*7 邻接矩阵：

完整代码

% 构造邻接矩阵
a = zeros(7);
a(1,2) = 2; a(1,3) = 4;
a(2,4) = 3; a(2,5) = 3; a(2,6) = 1;
a(3,4) = 2; a(3,5) = 3; a(3,6) = 1;
a(4,7) = 1;
a(5,7) = 3;
a(6,7) = 4;
a = a + a';
a(a==0) = inf; % 零元素换成inf
a(eye(7,7)==1)=0; % 对角线换成 0 

[mydist1,mypath1]=mydijkstra(a,1,7) % dijkstra模型求解
[mydist2,mypath2]=myfloyd(a,1,7) % floyd 模型求解

运行结果

mydist1 =

     6


mypath1 =

     1     2     4     7


mydist2 =

     6


mypath2 =

     1     2     4     7

将序号还原成点位，即最短路径为 A → B1 → C1 → D

转载于:https://www.cnblogs.com/gshang/p/11512005.html