详解如何使用Python绘制动图（一）|解析FuncAnimation接口用法以及实践

---

在这篇文章中，我们将熟悉并使用Matplotlib提供的animation模块，绘制动态图像。

我们将绘制一个简单的例子：在正弦函数上移动的切线。

---

一. FuncAnimation接口与绘图思路

1. FuncAnimation接口

FuncAnimation是Matplotlib库为我们提供的用于绘制动态图像的接口，其中包含如下参数：

• fig：画布对象，由创建画布时的返回得到，即fig = plt.figure()
• frames：指定动图的帧数，但这个参数类型必须是可迭代的列表等。每次调用func函数对图像进行更新时，接口将自动向func函数提供此时的帧数num，这使得更新数据十分方便。
• func：用于更新图片从而产生动态效果的调用函数，在编写时通常会用到set_data等类似的方法，其返回值是一个元素为被更新的图形对象的列表。同时，func可以接受帧数参数num，用来更新每帧图像。具体内容我们将在示例中看到。
• interval：更新频率，单位是毫秒。

上面这些参数的用法我们会在具体的实践中更清楚的看到。

---

2. 绘图思路

(1). 绘制初始的静态图形

在绘制动态效果前，我们需要一个初始的静态的图片，例如在绘制正弦函数上变化的切线时，我们的初始图片是一条正弦函数曲线、在曲线第一个点上的切线以及对应的切点。在后续的动图中，切点与切线是变化的，也就是说，我们需要操作切点与切线这两个对象。

我们使用plot接口来绘制初始的正弦曲线、切点与切线，而实现后续的动态效果时，我们只需要更新绘制切点与切线时的数据即可。这就告诉我们，我们需要得到切点与切线的对象：

crave_ani = plt.plot(x,y,'red',alpha=0.5)[0]		#正弦曲线
tangent_ani = plt.plot(xs,ys,c='blue',alpha=0.8)[0]		#切线
point_ani = plt.plot(0,0,'r',alpha=0.4,marker='o')[0]		#切点

（由于这只是示例，我们先不需要搞清楚绘制切线的数据是怎么得到的。）

我们用crave_ani、tanget_ani和point_ani这三个变量来表示从plot接口中返回的三个对象。值得注意的是，plot接口可以同时绘制多个对象（例如两条曲线同时绘制时），所以它的返回是一个列表，而我们需要使用列表的方式来获得其中的元素。这也是其它文章中出现这种写法的原因：

crave_ani, = plt.plot(x,y,'red',alpha=0.5)

在crave_ani后加一个逗号，实际上就是用来从plot接口返回的列表中获得第一个元素。

---

(2). 在func函数中更新数据以获得动态效果

当我们使用plot接口绘制了多个图形后，我们需要从中选择需要更新数据的图形。在我们的例子中，切线和切点是需要更新的，而我们已经有了代表它们的变量。这时，我们只需要在func函数中使用set_data方法，例如

point_ani.set_data(x[num],y[num])

在上面这句代码中，num是实时的帧数，我们在使用FuncAnimation接口时，这个参数是自动返回给func函数的。列表x和y则是我们提前计算的坐标值。我们只需要使用set_data方法即可快速的通过帧数来更新切点的数据。

在func函数中，我们需要将被更新的图形对象以诸如列表等可迭代的数据形式返回，例如

return [point_ani]

这句代码表示我们在func函数中更新了一个图形对象的数据，我们需要把它们组成列表返回。在其它文章中，可能出现这样的写法：

return point_ani，

这种写法实际上是将被改变的图形对象作为元组返回，总之，返回值必须是可迭代的。

---

(3). 调用FuncAnimation接口

在完成初始图像绘制并在func函数中实现数据更新后，我们调用FuncAnimation接口即可。例如

ani = animation.FuncAnimation(fig=fig,func=updata,frames=np.arange(0,100),interval=100)

需要注意的是，帧数的指定一定需要使用可迭代的数据类型。

---

在完成这些工作后，我们可以进行保存、展示等操作：

ani.save('sin_x.gif')
plt.show()

---

二. 实践：绘制正弦曲线上变化的切线与切点

首先，我们调入需要的模块。numpy模块为我们提供快捷的矩阵计算，而matplotlib库中的pyplot模块和animation模块则分别提供静态与动态图形的绘制方法：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

之后，我们对画布进行初始化：

fig = plt.figure()
plt.grid(ls='--')

完成画布的简单初始化后，我们开始绘制初始图形。首先是一条正弦曲线：

x = np.linspace(0,2*np.pi,100)
y = np.sin(x)

crave_ani = plt.plot(x,y,'red',alpha=0.5)[0]

之后绘制切点：

point_ani = plt.plot(0,0,'r',alpha=0.4,marker='o')[0]

为了使得动图效果更好，我们在画布上增加坐标值以及切线斜率的文字标识，这些标识也将是动态的：

xtext_ani = plt.text(5,0.8,'',fontsize=12)
ytext_ani = plt.text(5,0.7,'',fontsize=12)
ktext_ani = plt.text(5,0.6,'',fontsize=12)

最后，我们来绘制切线的斜率，这里我们用到了几个函数。首先是通过顶点与斜率计算整条切线的函数，这个函数计算定点附近的切线上的值，用来绘制切线：

def tangent_line(x0,y0,k):
	xs = np.linspace(x0 - 0.5,x0 + 0.5,100)
	ys = y0 + k * (xs - x0)
	return xs,ys

之后我们还需要一个计算定点处切线斜率的函数，我们使用了简单的估计：

def slope(x0):
	num_min = np.sin(x0 - 0.05)
	num_max = np.sin(x0 + 0.05)
	k = (num_max - num_min) / 0.1
	return k

最后，调用这些函数和plot接口即可：

k = slope(x[0])
xs,ys = tangent_line(x[0],y[0],k)
tangent_ani = plt.plot(xs,ys,c='blue',alpha=0.8)[0]

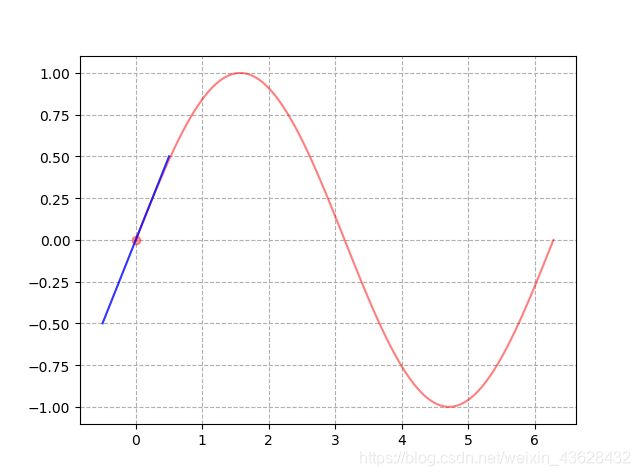
此时，我们的初始图形绘制完成了，其效果是这样的：

下面，我们开始写用来更新数据的func函数：

def updata(num):
	k=slope(x[num])
	xs,ys = tangent_line(x[num],y[num],k)
	tangent_ani.set_data(xs,ys)
	point_ani.set_data(x[num],y[num])
	xtext_ani.set_text('x=%.3f'%x[num])
	ytext_ani.set_text('y=%.3f'%y[num])
	ktext_ani.set_text('k=%.3f'%k)
	return [point_ani,xtext_ani,ytext_ani,tangent_ani,k]

其中，我们利用set_data和set_text方法来更新切线、切点以及文字内容，而这些数据都通过帧数num与计算得到的坐标值挂钩。熟练的使用set_data方法使我们的func函数形式优美。

最后，我们只需调用FuncAnimation接口即可获得动态效果：

ani = animation.FuncAnimation(fig=fig,func=updata,frames=np.arange(0,100),interval=100)
ani.save('sin_x.gif')
plt.show()

效果如下：

三. 完整代码

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#初始化画布
fig = plt.figure()
plt.grid(ls='--')

#绘制一条正弦函数曲线
x = np.linspace(0,2*np.pi,100)
y = np.sin(x)

crave_ani = plt.plot(x,y,'red',alpha=0.5)[0]

#绘制曲线上的切点
point_ani = plt.plot(0,0,'r',alpha=0.4,marker='o')[0]

#绘制x、y的坐标标识
xtext_ani = plt.text(5,0.8,'',fontsize=12)
ytext_ani = plt.text(5,0.7,'',fontsize=12)
ktext_ani = plt.text(5,0.6,'',fontsize=12)

#计算切线的函数
def tangent_line(x0,y0,k):
	xs = np.linspace(x0 - 0.5,x0 + 0.5,100)
	ys = y0 + k * (xs - x0)
	return xs,ys

#计算斜率的函数
def slope(x0):
	num_min = np.sin(x0 - 0.05)
	num_max = np.sin(x0 + 0.05)
	k = (num_max - num_min) / 0.1
	return k

#绘制切线
k = slope(x[0])
xs,ys = tangent_line(x[0],y[0],k)
tangent_ani = plt.plot(xs,ys,c='blue',alpha=0.8)[0]

#更新函数
def updata(num):
	k=slope(x[num])
	xs,ys = tangent_line(x[num],y[num],k)
	tangent_ani.set_data(xs,ys)
	point_ani.set_data(x[num],y[num])
	xtext_ani.set_text('x=%.3f'%x[num])
	ytext_ani.set_text('y=%.3f'%y[num])
	ktext_ani.set_text('k=%.3f'%k)
	return [point_ani,xtext_ani,ytext_ani,tangent_ani,k]

ani = animation.FuncAnimation(fig=fig,func=updata,frames=np.arange(0,100),interval=100)
ani.save('sin_x.gif')
plt.show()