算法设计与应用实训-城市公交站点及换乘方案设计
1、任务内容
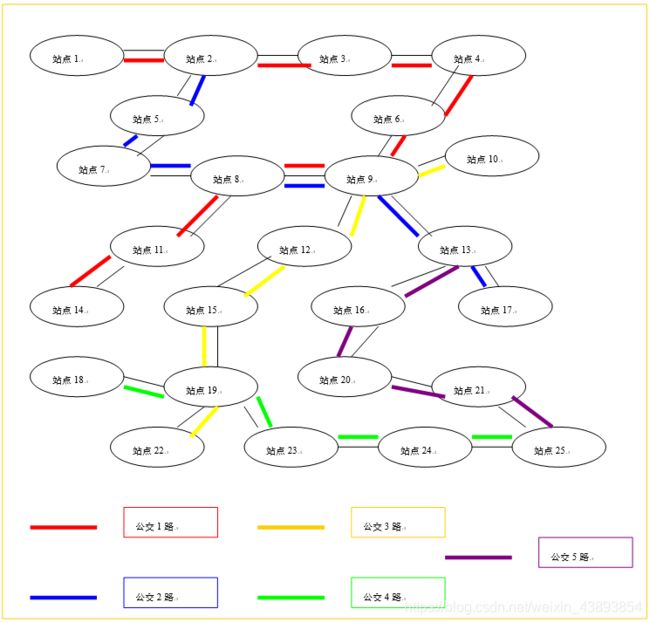
城市公共交通站点,站点之间的道路,及道路长度实际构成数学意义上的无向加权图。现请设计实现一个算法,求任意两站点间最短路径距离且输出该最短路径上的每个站点,然后给一个乘车换乘方案。
2、需求分析
(1)显示站点信息:输入某个站点,程序显示停靠该站点的公交线路。
(2)显示公交信息:输入某个公交线路,程序显示该线路所经过的站点。
(3)查询出行方案:输入起始站和终点站,程序给出最短的路线,同时给出公交乘车及换乘的方案。
3、程序设计
(1)数据结构:
struct Point //站点
{
int no; //公交站点编号
char board[5]; // 站牌:该站有哪几路公交车经过
};
struct MatGraph //图的邻接矩阵类型
{
int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数、边数
Point poi[MAXV]; //站点信息
};
创建一个无向不带权图。其中,用邻接矩阵来存储站点样图中的路径信息;每个站点用一个数组来记录有哪几路公交车经过,若公交1路经过站点1,则poi[0].board[0]=1,若不经过则为0。
(2)功能实现:
①显示站点信息:
输入某个站点,程序遍历该站点的board数组,若board[i]=1,则说明公交线路i-1停靠该站点,将该线路输出。
②显示公交信息:
程序遍历该公交线路n的poi数组,若poi[i].board[n-1]=1,则说明公交线路i-1停靠该站点,将该站点输出。
③查询出行方案:
无向图存储完毕后,调用Floyd算法,用两个矩阵D[][]、P[][]记录每两个站点间的最短路径和中转点。输入起始站a和终点站b,记录当前站点now为起始站存储位a-1,记录下一站next为a到b的第一个中转点P[a-1][b-1]。比较now和next站点的board数组,如果这两个站点的board[i]都为1,即两个站点有相同公交线路,则乘坐该线路向前。记录下当前乘坐的线路j。之后进入循环,更新当前站now为next,更新下一站next为新的中转点即P[now][b-1]。继续比较两个站点是否有相同线路。比较中,如果当前乘坐的线路与之前记录的线路j不同,则视为换乘。继续该循环直到下一站next为终点站存储位b-1,出行方案显示完成。
4、遗留及待优化问题
(1)邻接矩阵存储线路信息,图的边数少,浪费大量内存空间,若使用邻接表形式则会更加节省空间。
(2)使用普通数组存储公交车信息,浪费内存空间。可使用bfs或dfs等算法降低空间开销。
(3)无法做到查询最少换乘方案的功能。
完整代码
//2019-2020学年第二学期 算法设计与应用实训
#include仅作留档。