POJ-3281 Dining【网络流】【最大流】【dinic】

题目

POJ-3281

题意

n只牛，f种食物，d种食物，每只牛都有喜欢的食物和饮料，每头牛都有各自喜欢的食物和饮料，每种食物或饮料只能分配给一头牛。问最多能有多少头牛可以同时得到喜欢的食物和饮料。（每头牛只吃一份食物和饮料）

题解

建一个像下面的图求最大流（边权都为1）

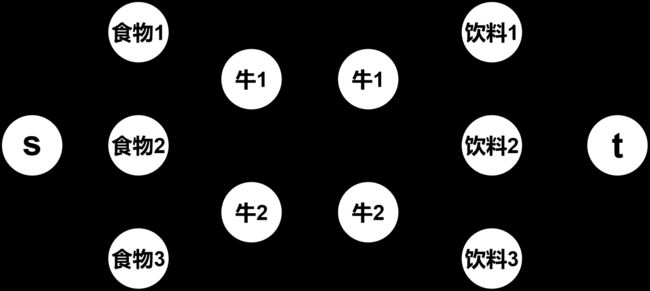
主要讲下为什么要把每只牛拆开成两部分
如果不拆的话会建立如下的图，这样子求出的最大流为2，因为一只牛吃了两份食物饮料，把牛拆开来限制了一只牛只能吃一份食物饮料

代码

/*
 * @author: arc
 * @date: 2020-08-11 16:44:45
 */
#include
#include
#include
using namespace std;
#define INF 0x3f3f3f3f
const int maxn = 4e6+5;

int n, m, deep[maxn];//n点的数量, deep深度
struct Edge{
    int next, to, flow;
}edge[maxn];

int num_edge = -1, head[maxn];//head从1开始建点
queue<int> q;//用于bfs

void init() { memset(head, -1, sizeof(head)); }

void add_edge(int from, int to, int flow, bool flag) {//flag为1建正边，flag为0建反边
    edge[++num_edge].next = head[from];
    edge[num_edge].to = to;
    if(flag) edge[num_edge].flow = flow;//反边权值为0
    else edge[num_edge].flow = 0;
    head[from] = num_edge;
}

//bfs用来建分层图
bool bfs(int s, int t) {//s起点，t终点
    memset(deep, 0, sizeof(deep));//深度初始化为0
    while(!q.empty()) q.pop();
    deep[s] = 1;
    q.push(s);
    while(!q.empty()) {
        int now = q.front(); q.pop();
        for (int i = head[now]; i != -1; i = edge[i].next) {//遍历当前点的所有出边
            if (!deep[edge[i].to] && edge[i].flow){//该点没有标记过深度且该边还有剩余容量
                deep[edge[i].to] = deep[now]+1;
                q.push(edge[i].to);
            }
        }
    }
    if(deep[t]) return true;//如果bfs搜索不到终点t的的深度，就说明当前图已经不存在增广路径
    else return false;
}

//dfs找当前图的增广的容量
int dfs(int now, int t, int fl) {//t终点，fl当前点的流量
    if(now == t) return fl;
    int f = 0;//该点dfs求的最小流量
    for (int u = head[now]; u!=-1&&fl; u = edge[u].next){
        if(edge[u].flow && deep[edge[u].to] == deep[now]+1){
            int x = dfs(edge[u].to, t, min(edge[u].flow, fl));
            edge[u].flow -= x;//正边流量减少
            edge[u ^ 1].flow += x;//反边增加
            fl -= x;
            f += x;
        }
    }
    if (!f) deep[now] = -2;
    return f;
}

int Dinic(int s, int t) {
    int maxflow = 0;
    while (bfs(s, t)) {
        maxflow += dfs(s, t, INF);
    }
    return maxflow;
}

int main() {
    int nn, ff, dd;
    init();
    scanf("%d%d%d", &nn, &ff, &dd);
    int s = 1, t = 1 + ff + nn * 2 + dd + 1;
    int from, to;
    int fn, dn;
    for (int i = 1; i <= ff; i++) {
        add_edge(s, s + i, 1, 1);
        add_edge(s + i, s, 0, 0);
    }
    for (int i = 1; i <= nn; i++) {
        from = 1 + ff + i;
        to = 1 + ff + nn + i;
        add_edge(from, to, 1, 1);
        add_edge(to, from, 0, 0);
    }
    for (int i = 1; i <= dd; i++) {
        from = 1 + ff + 2 * nn + i;
        add_edge(from, t, 1, 1);
        add_edge(t, from, 0, 0);
    }
    for (int i = 1; i <= nn; i++){
        scanf("%d%d", &fn, &dn);
        to = 1 + ff + i;
        for (int j = 1; j <= fn; j++){
            scanf("%d", &from);
            from += 1;
            add_edge(from, to, 1, 1);
            add_edge(to, from, 0, 0);
        }
        from = 1 + ff + nn + i;
        for (int j = 1; j <= dn; j++) {
            scanf("%d", &to);
            to += 1 + ff + nn + nn;
            add_edge(from, to, 1, 1);
            add_edge(to, from, 0, 0);
        }
    }
    int ans = Dinic(s, t);
    printf("%d\n", ans);
    return 0;
}