汉诺塔c语言做法：汉诺塔（Hanoi）是必须用递归方法才能解决的经典问题。它来自于印度神话。上帝创造世界时作了三根金刚石柱子，在第一根柱子上从下往上按大小顺序摞着64片黄金圆盘

汉诺塔（Hanoi）是必须用递归方法才能解决的经典问题。借助c杆将所有的圆盘移到b杆上，每次只能移一个，且小的盘子一定在大的盘子上面

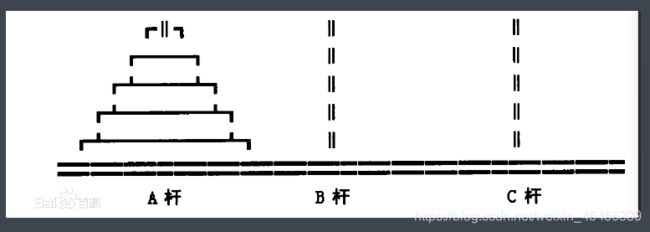
它来自于印度神话。上帝创造世界时作了三根金刚石柱子，在第一根柱子上从下往上按大小顺序摞着64片黄金圆盘，如图所示。上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放到第二根柱子上，并且规定，每次只能移动一个圆盘，在小圆盘上不能放大圆盘。有人预言说，这件事完成时宇宙会在一瞬间闪电式毁灭，也有人相信婆罗门至今仍在一刻不停地搬动着圆盘。

思考关键词：（结合代码看文字理解更快）

1. 目标柱
2. 转移柱
3. 盘子的序号：从上往下 1 —> n！！
4. 负担
5. 柱子的序号：从左往右 A —> B —> C

（ 6. 整体的思考，隐形的思考——）

思路详叙：【结合代码看思路更快】

【注意】画图可能会有多种移动方式，但是记住递归函数的本质，是有一定规律的，可以套用自己的，注意选择并找到正确的画图方式
//
//

• 初拿到这道题的时候，因为要求使用递归，所以自然而然的想到去找规律，于是画了很多图，从1个开始画到了三个，步骤就有些多了，然后开始找规律
• 当只有一个盘子的时候，只需要将其移动到中间的目标柱子上。当两个盘子的时候，就需要借助转移柱来把第二个盘子移到目标柱，如第二行图。
• 当三个盘子的时候，为了把三号盘子转移到目标柱上面，必须把上面的负担先转移，也就是把一号盘子与二号盘子先转移到转移柱上，这样三号盘子才可以动。而关键的一点就是，此时假想三号盘子不在，只有一二号盘子，那么上一句话提到的转移柱（一号盘子和二号盘子）对他们来说就是目标柱，在回想两个盘子的移动过程，就会发现：当有三个盘子的时候，假设三号盘子隐形，就会出现两个盘子要移动到一个目标柱上面的情形。
• 此时在回忆对于递归函数的理解：自己调用自己，用自己的一部分来表示自己（形象理解：字典就是一个递归，字典有汉字组成，用来解释别的成语也是有汉字组成）
• 我们在上面发现了一点规律之后，就可以推广，联想两个盘子的时候，当有 n个盘子的时候，我们也会想把最下面的盘子先移动到目标柱子上。此时完全可以类推，上面的 n-1 个盘子为一个整体，先把这部分放到转移柱上，然后才可以把 n 号盘子转移到目标柱上。
• 而把 n-1 个盘子转移到转移柱上，联想三个盘子的情形，需要借助另一个‘转移柱’才可以转移成功。此时就是转移柱和目标柱的转换
• n-1 ，n-2 一直这样往回想下去，就会想到剩三个盘子的情形，就是递归函数的递归实现了
  …

简而言之

只有三个柱子，只有一个转移柱，和一个目标柱，再多的盘子，都是在转移柱的帮助下实现的转移，其实就只有三步-（联想一下两个盘子的情形）-，上面的盘子到转移柱上去，底下的盘子到目标柱上去，上面的盘子再回来，这其实都是对称的过程，在转换过程中，每一个盘的目标柱和转移柱有转换的关系。可以用隐形盘子的想法，简单想把上面的盘子移到一个柱子之后在出现一个盘子，这时候的这个盘子就可以直接移到剩下的一根光秃秃的柱子上。（也可以想整体的思路，永远把上面的 n-1个盘子当成整体，往里套，最后在只有一个盘子的时候结束）

代码在此

要写递归函数强调一下递归函数的作用一定要明确
递归函数的出口要明确
递归的规律一定要写清楚

#include 
int i = 1;
void hannuo(int n,char a,char b,char c)//作用：打印把第n块移到目标的过程
{          //            目标柱  转移柱【针对编号为n的盘子】
    if (n == 1) {
        printf("%d[%d]: %c --> %c\n",i++,n,a,c);//第一次的时候，因为不断在调用，所以这里就是出口
    }
    else
    {
        hannuo(n-1, a,    c,     b);
        //                     目标柱【针对编号为n-1的盘子】为给n号盘子让路
        printf("%d[%d]: %c --> %c\n",i++,n,a,c);
        //就是该函数的目的：打印第n块被移到目标柱上
        hannuo(n-1, b, a, c);
        //依然从n-1号盘子开始往里调用，直到最后一个一号盘子归位结束递归函数
    }
}
int main ( )
{
    static int n;//静态全局变量的说明,当然可以不用，用全局变量写在外面就好。
    
    scanf("%d",&n);
    hannuo(n,'A','C','B');
}

运行结果

简洁版代码

#include 
int i = 1;
int n;
void hannuo(int n,char a,char b,char c)
{   
    if (n == 1) {
        printf("%d[%d]: %c --> %c\n",i++,n,a,c);
    }
    else
    {
        hannuo(n-1, a,    c,     b);
	    printf("%d[%d]: %c --> %c\n",i++,n,a,c);
        hannuo(n-1, b, a, c);
    }
}
int main ( )
{
	scanf("%d",&n);
    hannuo(n,'A','C','B');
    
}

**总结：**多练习递归，理解递归函数，在熟练运用，明白递归函数的三要素。

心得感悟（心里想逼逼的话）：

这个真的不好理解啊，递归和汉诺，但是总算体会到老师说的话，多看别的资料，多结合起来思考，其实我也是白读了好多关于递归的文章，加上一开始自己的执迷不悟，画了半天图，才感觉到那么一点点汉诺塔的思路。在查阅资料的过程中，不要只局限于一种思考方式，多多尝试。有时候单看文字会比较难理解，我觉得代码可以帮助理解。

附言：才开始学一点c语言，还不太熟练，前面文章中可能讲的不太清晰，还请海涵。