【计算方法笔记】四阶Runge-Kutta法
四阶Runge-Kutta法用于求常微分方程的较高精度的数值解。在高等数学里是用解析法来求解常微分方程问题,如下
y ′ ( x ) = f ( x , y ) , a ≤ x ≤ b y'(x)=f(x,y),a\leq x\leq b y′(x)=f(x,y),a≤x≤b
y ( a ) = y 0 y(a)=y_0 y(a)=y0
而在计算方法里,只要常微分方程解存在并唯一,即可求解数值解:
就是求 y ( x ) y(x) y(x)在区间[a,b]中一系列离散点上 y ( x k ) y(x_k) y(xk)的近似值 y k y_k yk.
具体步骤是,从已知条件 y ( a ) = y 0 y(a)=y_0 y(a)=y0出发,先求 y 1 y_1 y1,在求 y 2 y_2 y2,以此类推直至求出 y n y_n yn.这种顺着节点的排列顺序一步步向前步进的方法称为步进法。步进法又有单步法和多步法。
欧拉公式
首先将求导区间[a,b]分为n等分, b − a n = h \frac{b-a}{n}=h nb−a=h,则 x i = a + i h x_i=a+ih xi=a+ih
欧拉公式分为前进欧拉公式和后退欧拉公式
欧拉公式是基于数值微分的两点公式计算而来的,前进欧拉公式是利用了前进差分公式,后退欧拉公式使用了向后差分的公式。而且利用后退欧拉公式得到的是隐函数,还需要再解方程。
所以通常情况下,我们要采用显示和隐示结合起来,即通过显示求出的值带入隐式中,求得最终的结果。
$\overline{y}=y_{k-1}+hf(x_{k-1},y_{k-1}) $,预测值
y k = y k − 1 + h f ( x k , y ‾ ) y_k=y_{k-1}+hf(x_k,\overline{y}) yk=yk−1+hf(xk,y),校正值
y ( x 0 ) = y 0 , k = 1 , 2 , . . . . y(x_0)=y_0,k=1,2,.... y(x0)=y0,k=1,2,....
改进的欧拉法具有二阶精度
对于最开始提到的常微分方程的解法,也可以表示为积分的形式
∫ x k − 1 x k y ′ ( x ) d x = y ( x k ) − y ( x k − 1 ) \int_{x_{k-1}}^{x_k}y'(x)dx=y(x_k)-y(x_{k-1}) ∫xk−1xky′(x)dx=y(xk)−y(xk−1)
y ( x k ) = y ( x k − 1 ) + ∫ x k − 1 x k f ( x , y ( x ) ) d x y(x_k)=y(x_{k-1})+\int_{x_{k-1}}^{x_k}f(x,y(x))dx y(xk)=y(xk−1)+∫xk−1xkf(x,y(x))dx
而对于积分可以利用梯形法来求,然后因为梯形法是隐式的所以我们需要显化,就如同上述的欧拉法建立预测校正系统。
Runge-Kutta法
上述的改进欧拉法为二阶的R-K法,同时可对Simpson公式进行显化得到更高精度的R-k法。
四阶的R-K法
题目:求 y ′ ( x ) = 1 2 ( − y + x 2 + 4 x − 1 ) y'(x)=\frac{1}{2}(-y+x^2+4x-1) y′(x)=21(−y+x2+4x−1), y ( 0 ) = 0 y(0)=0 y(0)=0,x属于[0.0.5]区间内。求y(x)在xi=ih(h=0.05)处的数值解,并于解析解进行比较
下面为python代码,根据公式进行简单计算即可
import numpy as np
import math
import matplotlib.pyplot as plt
plt.style.use("seaborn-whitegrid")
def F(x,y):#定义函数
tem=0.5*(-y+x**2+4*x-1)
return tem
n=10
h=0.5/n
y=np.zeros(n+1,dtype='float32')#这样定义可以用y[i]访问,若定义为(1,n),则要用y[0][i]访问,因为维度问题
x=np.arange(0,0.5+0.05,0.05,dtype='float32')
# test=np.zeros((1,8))
# test[0][1]#right
# test[1]#wrong
for i in range(1,n+1,1):
K1=F(x[i-1],y[i-1])
K2=F(x[i-1]+h/2,y[i-1]+(h*K1)/2)
K3=F(x[i-1]+h/2,y[i-1]+(h*K2)/2)
K4=F(x[i-1]+h,y[i-1]+h*K3)
y[i]=y[i-1]+h*(K1+2*K2+2*K3+K4)/6
real=np.zeros(n+1)
for i in range(1,n+1,1):
real[i]=math.exp(-x[i]/2)+x[i]**2-1
error=abs(real-y)
plt.figure(1)
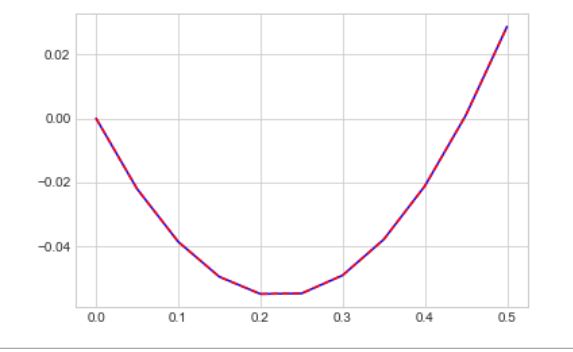
# plt.plot(x,real,'b')
# plt.plot(x,y,'r--')#不需要hold on命令
plt.plot(x,error)
plt.show()
#基本上吻合
可见四阶的R-K精度比较高的