计算理论总结
计算理论复习
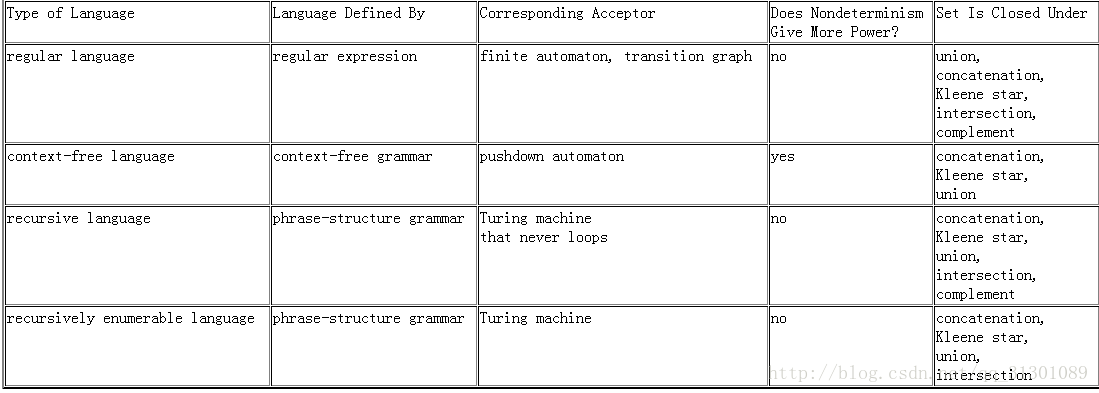
正则语言与有穷自动机
- 可数无穷
- 正则表达式(注意+不是正则,*是正则; L∅=∅L=∅ )
Σ⋃{(,),∅,⋃,∗} - DFA
- M = ( K , Σ , δ , s , F ) where
K is a finite set of states,
Σ is an alphabet,
s∈K is the initial state,
F⊆K is the set of final states,
δ is the transition function form K×Σ to K
- M = ( K , Σ , δ , s , F ) where
- NFA
- M = ( K , Σ , Δ , s , F ) where
K is a finite set of states,
Σ is an alphabet,
s∈K is the initial state,
F⊆K is the set of final states,
Δ is the transition relation form K×(Σ⋃{e})×K to K
- for each NFA, there is an equivalent DFA
(将NFA的状态的集合变为DFA中的点)
- for each NFA, there is an equivalent DFA
- M = ( K , Σ , Δ , s , F ) where
- closure 和 pumping theory
- The class of languages accepted vy finite automata is closed under:
- union
- concatentenation
- Kleene star
- complementation
- intersection
- A language is regular if and only if it is accepted by finite automaton
正则表达式和DFA, NFA的相互转化按照步骤生成 - Pumping Theory: Let L be a regular language. There is an integer n≥1 such that any string w∈L with |w|≥n can be rewritten as w=xyz such that y≠e,|xy|≤n , and xyiz∈L for each i≥0
- The class of languages accepted vy finite automata is closed under:
Give DFA or NFA write Regular Expression
Give regular expression, write DFA or NFA
Show a given language is (construct) or is not regular (pumping)context-free and pushdown自动机
- context-free grammar
- G = ( V , Σ , R , S ) where
V is an alphabet
Σ is the set of terminals, is a subset of V
R is the set of rules (V−Σ)×V∗
S is the start Symbol, is an element of V−Σ - all regular languages are context-free
- parse tree, leftmost derivation, rightmost derivation
Grammars with strings that have two or more distinct parse trees are called ambiguous
- G = ( V , Σ , R , S ) where
PDA
M = ( K , Σ , Γ , Δ , s , F ) where
K is a finite set of states
Σ is an alphabet (the input symbols)
Γ is an alphabet (the stack symbols)
s∈K is initial state
F⊆K is the set of final states
Δ is the transition relation (K×(Σ⋃{e})×Γ∗)×(K×Γ∗)The class of languages accepted by PDA is exactly the class of context-free languages
The transitions from CFL to PDA:- ((p,e,e),(q,S))
- ((q,e,A),(q,x)) for each rule A→x in R
- ((q,a,a),(q,e)) for each a∈Σ.
- clousure, pumping theory
- CFL are closed under union, concatenation, Kleene star, CFL在补和交上不封闭
- CFL与正则的交集为CFL
- pumping theory: Let G = ( V , Σ , R , S ). Then any string w∈L(G) of length greater than ϕ(G)|V−Σ| can be written as w=uvxyz in such a way that either v or y is nonempty and uvnxynz is in L(G) for every n≥0
Given context-free language, write context-free grammar and PDA
Give context-free grammar, write PDA
Show a given language is or is not Context-free- context-free grammar
Turing Machine and Recursive Enumerable Language
Turing machine
- M = ( K , Σ , δ , s , H ) where
K is a finite set of states
Σ is an alphabet, containing the blank symbol ⨆ and the left end symbol ⊳ , but not containing the symbol → and ←
s∈K is the initial state
H⊆K is the set of halting states
δ , the transition function (K−H)×Σ to K×(Σ⋃{→,←}) M decide L : if w∈L then M accepts w , and if w∉L then M rejects w
Call a language recursice if there is a TM decides it.- A function f is called recursive if there is a TM computes f
- M semidecides L : w∈L iif M halts on input w
Call a language recursicely enumerable iif there is a TM semidecides it. - if a language is recursive, then it is recursively enumerable
- the complement of recursive language is also recursive
- 多带和复合
Corollary: Any function that is computed or language that is decided or semidecided by a k-tape TM is also computed, decided or semidecided by a standard TM.
- M = ( K , Σ , δ , s , H ) where
- Grammar
- G = ( V , Σ , R , S ) where
V is an alphabet
Σ is the set of terminals, is a subset of V
R is the set of rules (V∗(V−Σ)V∗)×V∗
S is the start Symbol, is an element of V−Σ - a language is generated by a grammar iif it is recursively enumerable
递归可枚举只在补和差下不封闭 - G computes f , if: SwS⇒∗Gv iif v=f(w) .
A function f is called grammatically computable iif there is a grammar G computes it. - A fucntion f is recursive iif it is grammatically computable
- the transition form TM to Grammar? (P230)

- G = ( V , Σ , R , S ) where
- Numerical Function
- Basic Function:
- zero, zerok(n1,n2,...,nk)=0
- identity, idk,j(n1,n2,...,nk)=nj
- successor, succ(n)=n+1
- The primitive recursive functions are all basic functions, and all functions that can be obtained by them by any number of successive application of composition and recursive definition
- other primitive resursive funstion:
- plus(m,n)=m+n use m+n
- mult(m,n)=m∗n use m∗n
- exp(m,n)=mn use m↑n
- all constant functions of the form f(n1,...,nk)=17
- sgn(n) which is zero if n=0
- m∼n=max{m−n,0} (defined use a predecessor function pred(0)=0,pred(n+1)=n )
- primitive recursive predicate (primitive functions that only takes values 0 and 1):
- greater−than(m,n) , greater−than−or−equal(m,n) , equal(m,n)
- iszero(n) , isone(n) , positive(n)
- Those function’s negation, disjunction and conjunction are also primitive recursive predicates
- Funstion defined by cases:(can be written as)
f(n)=p(n)∗g(n)+(1∼p(n))∗h(n)
- rem(m,n) and div(m,n)
- not all computable functions are primitive recursive
- denote minimalization of g by μ m[g(n1,n2,...,nk,m)=1] The obvious method:
m:=0 ;
while g(n1,n2,...nk,m)≠1 do m:=m+1
output m
But it is not a algorithm becaues it may fail to terminate
- call a function g minimalizable if the above method always terminates.
- Call a function μ -recursive if it can be obtained form basic functions by operations of composition, recursive definition, and minimalization of minimalizable funtions.
- log(m,n)=μ p[greater−than−or−equal((m+2)↑p,n+1)]
- A function is μ -recursive iif it is recursive(that is, computable by a TM)
- Basic Function:
Design Turing machine to compute a function or decide (semidecide) a language
判断原始递归函数Undecidablity
- Church Turing Thesis
- 在所有输入上停机 ⇔ 算法
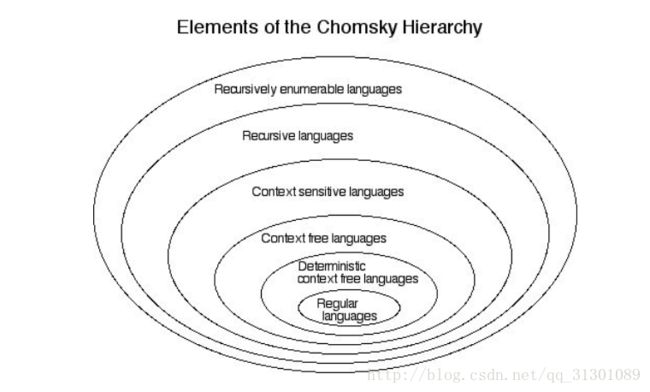
- Chomasky hierachy
- Universal Turing Machine
- Halting problem
- H={"M","w": TM M halts on input string w} is recursively enumerable
It is precisely the language semidecided by universal TM U. - The language H is not Recursive; therefore, the class of recursive languages is a strict subset of the class of recursively enumerable languages.
- The class of recursively enumerable languages is not closed under complement
- H={"M","w": TM M halts on input string w} is recursively enumerable
- Some Undecidable problem and Reduction
- 若有 X≤Y (X规约到Y), X 不可判定,则 Y 不可判定;Y 可判定, 则 X 可判定。
- Properites of recursive languages
- Rice

Show a given language be recursive enumerable
show a given language be not recursivelast one- Church Turing Thesis
来自总结的一些例子:
- a∗b∗c∗−{anbncn,n>=0} is context free but not regular
- L=L1L2 , L 是context free, 则 L1 一定是context free (x)
- Regular - context free不一定是CFL (如 a∗b∗c∗−anbn 包含 anbncn )
- 2-way PDA(i.e. PDA whose input head can move both left and right are more powerful than 1-way PDA
- Given a PDA M1 and an FA M2 , the problem L(M1)⊆L(M2) is deciable
- 非正则语言的kleen star也可能是正则的。
正则语言的子集也可能非正则。
递归与 μ 递归等价
- PDA中,若每一个格局至多有一个格局接在它后面,则为确定型的。
确定型CFL在补下封闭 - A countable union of regular languages is necessarily regular (x)
可数包含可数无穷 -

-

- 有时构造context-free不太好想时,通过构造PDA证之。

- It is decidable whether or not a given string belongs to a context-free language.
It is decidable whether or not a context-free language is empty.
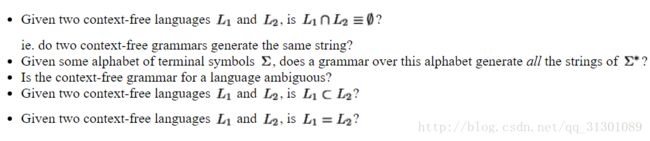
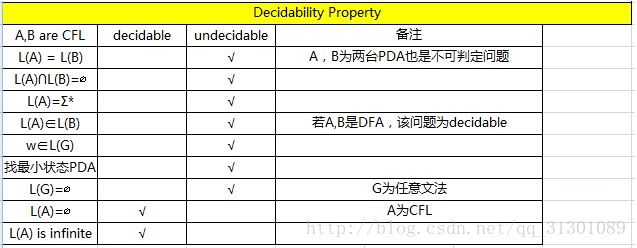
-

- pumping theory不能反过来证明是否正则或CFL
- If L1 is regular, L2 is not regular, then L1∘L2 must be non-regular (X)
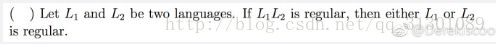
- 判断


- 对于非确定图灵机的n步,确定图灵机要用n的指数步来模拟
判断下面问题是否可判定
参考链接- 两个基本问题(前者为递归可枚举但不递归,后者不是递归可枚举)

- 一个图灵机至少有481个状态 (YES)
- 给定图灵机在空串上走了481步还没有停机 (YES)
- 给定图灵机,判断它是否在一些输入上经过481步还没有停机 (YES)
- 给定图灵机,判断它是否在所有输入上经过481步还没有停机 (YES)
- 给定图灵机是否接受空串 (NO)
- 给定TM M, 是否存在在M上停机的串? (NO)
给定TM M,M是否在所有串上停机? (NO) - 给定TM M,is L(M) finite? (NO)(通过取非?)
- 给定TM M, 带上是否出现过a(a ∈Σ )? (NO)
- 给定 M1,M2 ,他们是否在同一个字符串上停机? (NO)
- 给定M, 只要M接受w, M接受 wR (NO)
- {M||L(M)|>2}. 递归可枚举但不递归

- countable

- RE
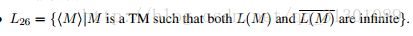
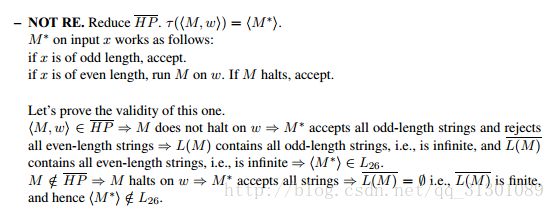

- 两个基本问题(前者为递归可枚举但不递归,后者不是递归可枚举)