数据库原理(八)- 关系代数
数据库原理(八)- 关系代数
- 前言
- 传统的集合运算
- 并(union)
- 差(except)
- 交(intersection)
- 笛卡尔积(cartesian product)
- 专门的集合运算
- 选择(selection)
- 投影(projection)
- 连接(join)
- 一般连接
- 等值连接 (equijoin)
- 自然连接(natural join)
- 外连接 (outer join)
- 左外连接 (left outer join)
- 右外连接 (right outer join)
- 除运算(division)
- 借鉴
前言
关系代数是一种抽象得抽象语言,它用作对关系德运算来表达查询。
任何一种运算都是讲一定的运算符作用与一定得运算对象上,得到预期的运算结果。所以运算对象、运算符、运算结果是运算的三大要素,而关系运算符分为传统运算符和专门运算符,如下图:
传统的集合运算
传统的集合运算属于二目运算,包括并、差、交、笛卡尔积4种运算。
我们首先假设有R和S两种关系,且相应的属性取自同一个域,t是元组变量,t∈R表示t是R的一个元组
R表:
| A | B | C |
|---|---|---|
| a1 | b1 | c1 |
| a1 | b2 | c2 |
| a2 | b2 | c1 |
S表:
| A | B | C |
|---|---|---|
| a1 | b2 | c2 |
| a1 | b3 | c2 |
| a2 | b2 | c1 |
并(union)
并的关系表达式为:
R∪S={t|t∈R∨t∈S}
我们将两张表代入关系表达式,得出以下结果:
R∪S
| A | B | C |
|---|---|---|
| a1 | b1 | c1 |
| a1 | b2 | c2 |
| a2 | b2 | c1 |
| a1 | b3 | c2 |
可知,并操作是将两张表的数据整合,消除重复列
差(except)
差的关系表达式为:
R-S={t|t∈R∧t∉ S}
将两张表代入关系表达式,得出以下结果
R-S
| A | B | C |
|---|---|---|
| a1 | b1 | c1 |
假如倒转一下,得出一下结果
S-R
| A | B | C |
|---|---|---|
| a1 | b3 | c2 |
可知,差操作是将被减表的数据去除,只保留减表的特有数据
交(intersection)
交的关系表达式为:
关系表达式 R∩S={t|t∈R∧t∈S}
将两张表代入关系表达式,得出下结果
R∩S
| A | B | C |
|---|---|---|
| a1 | b2 | c2 |
| a2 | b2 | c1 |
可知,交操作是将两张表的交集数据输出
笛卡尔积(cartesian product)
笛卡尔积的关系表达式为
R×S={tr ts|tr∈R∧ts∈S}
将两张表代入关系表达式,得出以下结果
R×S
| A | B | C | A | B | C |
|---|---|---|---|---|---|
| a1 | b1 | c1 | a1 | b2 | c2 |
| a1 | b1 | c1 | a1 | b3 | c2 |
| a1 | b1 | c1 | a2 | b2 | c1 |
| a1 | b2 | c2 | a1 | b2 | c2 |
| a1 | b2 | c2 | a1 | b3 | c2 |
| a1 | b2 | c2 | a2 | b2 | c1 |
| a2 | b2 | c1 | a1 | b2 | c2 |
| a2 | b2 | c1 | a1 | b3 | c2 |
| a2 | b2 | c1 | a2 | b2 | c1 |
可知,笛卡尔积的操作就是将乘表的所有元组与被乘表的元组都匹配一遍
专门的集合运算
专门的集合运算包括选择、投影、连接和除运算等,我们先给出几张表,等下在进行集合运算中更加清晰
学生表(student)
| 学号 | 姓名 | 性别 | 年龄 | 所在系 |
|---|---|---|---|---|
| 20170901 | 赵一 | 男 | 20 | cs |
| 20170902 | 钱二 | 女 | 20 | cs |
| 20170903 | 张三 | 男 | 19 | ma |
课程表(course)
| 课程号 | 课程名 | 先行课 | 学分 |
|---|---|---|---|
| 1 | 数据库 | 1 | 4 |
| 2 | 数学 | 1 | 2 |
| 3 | 信息系统 | 2 | 4 |
成绩表(sc)
| 学号 | 课程号 | 成绩 |
|---|---|---|
| 20170901 | 1 | 82 |
| 20170902 | 1 | 92 |
| 20170902 | 2 | 85 |
| 20170903 | 3 | 90 |
选择(selection)
选择又称为限制,它在关系R中选择满足给定条件的诸元组,记作
σF(R)={t|t∈R∧F(t)='真'}
其中F表示选择条件,它是一个逻辑表达式,取逻辑值”真“或”假“。
逻辑表达式F的基本形式为:
X₁θY₁ 其中θ表示为条件运算符,可以是 >、 ≧、<、 ≦、 = 和 <>(不等于)
举个例
查询年龄等于20岁的学生
σ 年龄列 = 20(学生表) // = 就是应用在关系式中的条件运算符
查询结果
| 学号 | 姓名 | 性别 | 年龄 | 所在系 |
|---|---|---|---|---|
| 20170901 | 赵一 | 男 | 20 | cs |
| 20170902 | 钱二 | 女 | 20 | cs |
在基本的选择条件之上还可以进一步的进行逻辑运算(∧与、∨或、¬非),比如
查询一个年龄等于20的男生
σ 年龄列 = 20(学生表) a ∧性别列 = 男(学生表)
查询结果
| 学号 | 姓名 | 性别 | 年龄 | 所在系 |
|---|---|---|---|---|
| 20170901 | 赵一 | 男 | 20 | cs |
投影(projection)
关系R上的投影是从R中选择若干属性列组成新的关系。记作
∏a(R)={t[A]}|t∈R}
其中A为R的属性列,投影操作是从列的角度进行的运算
举个例子
查询学生表中所有学生的学号和姓名
∏ 学号,姓名(学生表)
查询结果
| 学号 | 姓名 |
|---|---|
| 20170901 | 赵一 |
| 20170902 | 钱二 |
| 20170903 | 张三 |
连接(join)
连接也称为θ连接,它是从两个关系的笛卡尔积中选取属性间满足一定条件的元组。
这里假设两个关系,关系中有某些属性列相同,且值取自同一域
R
| A | B | C |
|---|---|---|
| a1 | b1 | 5 |
| a1 | b2 | 6 |
| a2 | b3 | 8 |
| a2 | b4 | 12 |
S
| B | E |
|---|---|
| b1 | 3 |
| b2 | 7 |
| b3 | 10 |
| b3 | 2 |
| b5 | 2 |
一般连接
在一般连接上,A和B分别为R和S上列数相等且可比的属性组,θ为比较运算符,记作
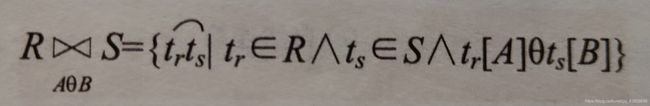
举个例子
输出 R⋈S 且C<E的元组
结果为
| A | R.B | C | S.B | E |
|---|---|---|---|---|
| a1 | b1 | 5 | b2 | 7 |
| a1 | b1 | 5 | b3 | 10 |
| a1 | b2 | 6 | b2 | 7 |
| a1 | b2 | 6 | b3 | 10 |
| a2 | b3 | 8 | b3 | 10 |
等值连接 (equijoin)
θ为“=”的连接运算称为等值连接。它是从关系R与S的广义笛卡尔积中选取A、B属性组值相等的那些元组,记作
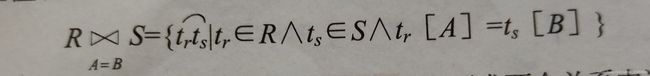
举个例子
R⋈S,且R.B=S.B
结果为
| A | R.B | C | S.B | E |
|---|---|---|---|---|
| a1 | b1 | 5 | b1 | 3 |
| a1 | b2 | 6 | b2 | 7 |
| a2 | b3 | 8 | b3 | 10 |
| a2 | b3 | 8 | b3 | 2 |
等值连接会去除属性列不相等的元组
自然连接(natural join)
自然连接是一种特殊的等值连接。它要求两个关系中进行比较的分量必须是同名的属性组,并在结果中把重复的属性列去掉,记作
![]()
举个例子
自然连接 R⋈S
结果为
| A | B | C | E |
|---|---|---|---|
| a1 | b1 | 5 | 3 |
| a1 | b2 | 6 | 7 |
| a2 | b3 | 8 | 10 |
| a2 | b3 | 8 | 2 |
外连接 (outer join)
两个关系自然连接时,选择两个关系的公共属性上的值相等的元组构成新的关系,而那些公共属性上的值不相等的元组就会被舍弃,这些被舍弃的元组称为悬浮元组。
如果把悬浮元组也保存在结果关系中,而在其他属性填空值(null),那么这种连接就叫做外连接
如R外连接S,结果为
| A | B | C | E |
|---|---|---|---|
| a1 | b1 | 5 | 3 |
| a1 | b2 | 6 | 7 |
| a2 | b3 | 8 | 10 |
| a2 | b3 | 8 | 2 |
| a2 | b4 | 12 | null |
| nul | b5 | null | 2 |
左外连接 (left outer join)
如果只保留左边关系R中的悬浮元组就叫做左外连接,如R⋊S,结果为
| A | B | C | E |
|---|---|---|---|
| a1 | b1 | 5 | 3 |
| a1 | b2 | 6 | 7 |
| a2 | b3 | 8 | 10 |
| a2 | b3 | 8 | 2 |
| a2 | b4 | 12 | null |
右外连接 (right outer join)
如果只保留右边关系S中的悬浮元组就叫做右外连接,如R⋉S,结果为
| A | B | C | E |
|---|---|---|---|
| a1 | b1 | 5 | 3 |
| a1 | b2 | 6 | 7 |
| a2 | b3 | 8 | 10 |
| a2 | b3 | 8 | 2 |
| nul | b5 | null | 2 |
除运算(division)
我们用象集来定义除法,首先给定关系R(X,Y)和S(Y,Z),其中X、Y、Z为属性组。R中的Y与S中的Y可以有不同的属性名,但必须出自相同的域集。
R与S的除运算得到一个新的关系P(X),P是R中满足下列条件的元组在X属性列上的投影:元组在X上x分量值x的象集Yx包含S在Y上投影的集合,记作
R÷S={tr [X]|tr∈R∧∏y(S)⊆Yx}
举个列子,这里先列出两张表
R
| A | B | C |
|---|---|---|
| a1 | b1 | c2 |
| a1 | b2 | c1 |
| a2 | b3 | c1 |
| a2 | b4 | c6 |
S
| B | C | D |
|---|---|---|
| a1 | b1 | d1 |
| a1 | b2 | d2 |
R÷S 解法
在关系R中,A可以取2个值{a1,a2}.其中:
a1的象集为{(b1,c2),(b2,c1)}
a2的象集为{(b3,c1),(b4,c6)}
S在(B,C)上的投影为{(a1,b1),(a1,b2)}
显然只有a1的象集(B,C)a₁包含了S在(B,C)属性组上的投影,所以R÷S={a₁}
结果为:
| A |
|---|
| a₁ |
除操作是同时从行和列的角度进行运算
借鉴
王珊,萨师煊.数据库系统概论(第五版)[M].北京:高等教育出版社,2014:48-56.
图片出自于书上
