基于NCNN的3x3可分离卷积再思考盒子滤波
【GiantPandaCV导语】这篇文章主要是对NCNN 的3x3可分离卷积的armv7架构的实现进行了非常详细的解析和理解,然后将其应用于 3 × 3 3\times 3 3×3盒子滤波,并获得了笔者最近关于盒子滤波的优化实验的最快速度,即相对于原始实现有37倍加速,希望对做工程部署或者算法优化的读者有一定启发。代码链接:
https://github.com/BBuf/ArmNeonOptimization
1. 前言
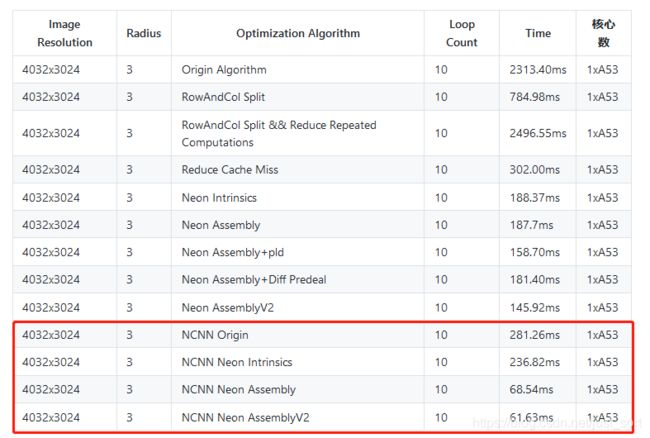
前面已经做了一系列实验来优化盒子滤波算法,然后经nihui大佬提醒去看了一下NCNN的 3 × 3 3\times 3 3×3深度可分离卷积算子的实现,在理解了这个代码实现之后将其拆分出来完成了一个 3 × 3 3\times 3 3×3的盒子滤波,并添加了一些额外的思考以及实现,最终在A53上将 3 × 3 3\times 3 3×3盒子滤波相对于最原始的实现加速了37倍,然后就有了这篇文章。完整速度测试结果如下:
上篇文章我们已经将半径为 3 3 3的盒子的滤波在A53上优化到了 145.92 m s 145.92ms 145.92ms,图像的分辨率是 4032 × 3024 4032\times 3024 4032×3024,所以本次系列实验的BaseLine已经明确,这一节就基于NCNN的convolutiondepthwise3x3.h将其核心代码拆出来实现这个盒子滤波,并对其做速度以及实现分析,所以也可以把这篇文章当成NCNN的 3 × 3 3\times 3 3×3可分离卷积算子实现代码分析。NCNN的convolutiondepthwise3x3.h地址为:https://github.com/Tencent/ncnn/blob/master/src/layer/arm/convolutiondepthwise_3x3.h 。
十分感谢德澎在我做这篇优化文章时的耐心指导以及指出一些关键指令的正确理解方式,学习路上拥有良师益友是十分幸运之事。
2. 原始实现—将盒子滤波看成卷积来做
实际上盒子滤波本来就是CNN中一个卷积的过程,只不过这里参与卷积的特征图通道数是1,然后卷积核固定为一个 3 × 3 3\times3 3×3的全 1 1 1矩阵,那么我们可以借助NCNN的https://github.com/Tencent/ncnn/blob/master/src/layer/arm/convolutiondepthwise_3x3.h展示的思路,将 3 × 3 3\times 3 3×3滤波核直接完全展开,一次读三行/四行来进行计算,这样做有个好处就是我们仍然规避掉了在行方向进行频繁切换导致的Cache Miss增加,并且在列方向可以做Neon加速。下面的代码展示了基于这一想法的普通实现版本,代码如下:
// 原始实现,一次读四行进行计算
void BoxFilterBetterOrigin(float *Src, float *Dest, int Width, int Height, int Radius){
int OutWidth = Width - Radius + 1;
int OutHeight = Height - Radius + 1;
//卷积核为全1矩阵,因为这里处理的是盒子滤波
float *kernel = new float[Radius*Radius];
for(int i = 0; i < Radius*Radius; i++){
kernel[i] = 1.0;
}
float *k0 = kernel;
float *k1 = kernel + 3;
float *k2 = kernel + 6;
float* r0 = Src;
float* r1 = Src + Width;
float* r2 = Src + Width * 2;
float* r3 = Src + Width * 3;
float* outptr = Dest;
float* outptr2 = Dest + OutWidth;
int i = 0;
//一次处理4行,对应2个输出
for (; i + 1 < OutHeight; i += 2){
int remain = OutWidth;
for(; remain > 0; remain--){
float sum1 = 0, sum2 = 0;
sum1 += r0[0] * k0[0];
sum1 += r0[1] * k0[1];
sum1 += r0[2] * k0[2];
sum1 += r1[0] * k1[0];
sum1 += r1[1] * k1[1];
sum1 += r1[2] * k1[2];
sum1 += r2[0] * k2[0];
sum1 += r2[1] * k2[1];
sum1 += r2[2] * k2[2];
sum2 += r1[0] * k0[0];
sum2 += r1[1] * k0[1];
sum2 += r1[2] * k0[2];
sum2 += r2[0] * k1[0];
sum2 += r2[1] * k1[1];
sum2 += r2[2] * k1[2];
sum2 += r3[0] * k2[0];
sum2 += r3[1] * k2[1];
sum2 += r3[2] * k2[2];
*outptr = sum1;
*outptr2 = sum2;
r0++;
r1++;
r2++;
r3++;
outptr++;
outptr2++;
}
r0 += 2 + Width;
r1 += 2 + Width;
r2 += 2 + Width;
r3 += 2 + Width;
outptr += OutWidth;
outptr2 += OutWidth;
}
for(; i < OutHeight; i++){
int remain = OutWidth;
for(; remain > 0; remain--){
float sum1 = 0;
sum1 += r0[0] * k0[0];
sum1 += r0[1] * k0[1];
sum1 += r0[2] * k0[2];
sum1 += r1[0] * k1[0];
sum1 += r1[1] * k1[1];
sum1 += r1[2] * k1[2];
sum1 += r2[0] * k2[0];
sum1 += r2[1] * k2[1];
sum1 += r2[2] * k2[2];
*outptr = sum1;
r0++;
r1++;
r2++;
outptr++;
}
r0 += 2;
r1 += 2;
r2 += 2;
}
}
由于原始实现非常简单,这里就不再赘述了,相信大家很容易就看懂了,这里打印了一下经过这个函数处理后的输出矩阵的前20个元素,值为:
308.00000 343.00000 360.00000 352.00000 330.00000 318.00000 327.00000 338.00000 331.00000 314.00000 304.00000 307.00000 323.00000 341.00000 348.00000 348.00000 350.00000 355.00000 355.00000 353.00000
然后处理完这张图片速度为281.26ms,可以从第一节的图中更直观的对比。
3. Neon Intrinsics 优化
将上面的原始实现的列方向进行Neon Intrinsics优化,德澎帮忙加了超详细注释的代码版本如下,不需要讲任何细节,因为细节确实都在代码和注释里:
void BoxFilterBetterNeonIntrinsics(float *Src, float *Dest, int Width, int Height, int Radius){
int OutWidth = Width - Radius + 1;
int OutHeight = Height - Radius + 1;
// 这里虽然 kernel 大小是根据输入设置
// 但是下面的计算写死了是3x3的kernel
// boxfilter 权值就是1,直接加法即可,
// 额外的乘法会增加耗时
float *kernel = new float[Radius*Radius];
for(int i = 0; i < Radius*Radius; i++){
kernel[i] = 1.0;
}
// 下面代码,把 kernel 的每一行存一个 q 寄存器
// 而因为一个 vld1q 会加载 4 个浮点数,比如 k012
// 会多加载下一行的一个数字,所以下面
// 会用 vsetq_lane_f32 把最后一个数字置0
float32x4_t k012 = vld1q_f32(kernel);
float32x4_t k345 = vld1q_f32(kernel + 3);
// 这里 kernel 的空间如果 Radius 设为3
// 则长度为9,而从6开始读4个,最后一个就读
// 内存越界了,可能会有潜在的问题。
float32x4_t k678 = vld1q_f32(kernel + 6);
k012 = vsetq_lane_f32(0.f, k012, 3);
k345 = vsetq_lane_f32(0.f, k345, 3);
k678 = vsetq_lane_f32(0.f, k678, 3);
// 输入需要同时读4行
float* r0 = Src;
float* r1 = Src + Width;
float* r2 = Src + Width * 2;
float* r3 = Src + Width * 3;
float* outptr = Dest;
float* outptr2 = Dest + OutWidth;
int i = 0;
// 同时计算输出两行的结果
for (; i + 1 < OutHeight; i += 2){
int remain = OutWidth;
for(; remain > 0; remain--){
// 从当前输入位置连续读取4个数据
float32x4_t r00 = vld1q_f32(r0);
float32x4_t r10 = vld1q_f32(r1);
float32x4_t r20 = vld1q_f32(r2);
float32x4_t r30 = vld1q_f32(r3);
// 因为 Kernel 最后一个权值置0,所以相当于是
// 在计算一个 3x3 的卷积点乘累加中间结果
// 最后的 sum1 中的每个元素之后还需要再加在一起
// 还需要一个 reduce_sum 操作
float32x4_t sum1 = vmulq_f32(r00, k012);
sum1 = vmlaq_f32(sum1, r10, k345);
sum1 = vmlaq_f32(sum1, r20, k678);
// 同理计算得到第二行的中间结果
float32x4_t sum2 = vmulq_f32(r10, k012);
sum2 = vmlaq_f32(sum2, r20, k345);
sum2 = vmlaq_f32(sum2, r30, k678);
// [a,b,c,d]->[a+b,c+d]
// 累加 这里 vadd 和下面的 vpadd 相当于是在做一个 reduce_sum
float32x2_t _ss = vadd_f32(vget_low_f32(sum1), vget_high_f32(sum1));
// [e,f,g,h]->[e+f,g+h]
float32x2_t _ss2 = vadd_f32(vget_low_f32(sum2), vget_high_f32(sum2));
// [a+b+c+d,e+f+g+h]
// 这里因为 intrinsic 最小的单位是 64 位,所以用 vpadd_f32 把第一行和第二行最后结果拼在一起了
float32x2_t _sss2 = vpadd_f32(_ss, _ss2);
// _sss2第一个元素 存回第一行outptr
*outptr = vget_lane_f32(_sss2, 0);
*outptr2 = vget_lane_f32(_sss2, 1);
//同样这样直接读4个数据,也会有读越界的风险
r0++;
r1++;
r2++;
r3++;
outptr++;
outptr2++;
}
r0 += 2 + Width;
r1 += 2 + Width;
r2 += 2 + Width;
r3 += 2 + Width;
outptr += OutWidth;
outptr2 += OutWidth;
}
for(; i < OutHeight; i++){
int remain = OutWidth;
for(; remain > 0; remain--){
float32x4_t r00 = vld1q_f32(r0);
float32x4_t r10 = vld1q_f32(r1);
float32x4_t r20 = vld1q_f32(r2);
//sum1
float32x4_t sum1 = vmulq_f32(r00, k012);
sum1 = vmlaq_f32(sum1, r10, k345);
sum1 = vmlaq_f32(sum1, r20, k678);
float32x2_t _ss = vadd_f32(vget_low_f32(sum1), vget_high_f32(sum1));
_ss = vpadd_f32(_ss, _ss);
*outptr = vget_lane_f32(_ss, 0);
r0++;
r1++;
r2++;
outptr++;
}
r0 += 2;
r1 += 2;
r2 += 2;
}
}
然后板端运行之后获得的输出矩阵的前20个元素为:
308.00000 343.00000 360.00000 352.00000 330.00000 318.00000 327.00000 338.00000 331.00000 314.00000 304.00000 307.00000 323.00000 341.00000 348.00000 348.00000 350.00000 355.00000 355.00000 353.00000
可以看到和原始实现是完全对应的,然后速度测试结果请看第一节的图,从281.26ms优化到了236.82ms。
4. Neon Assembly优化
将上面的代码对应翻译为Neon Assembly代码如下(实际上就是NCNN 的 3 × 3 3\times 3 3×3深度可分离卷积实现,不过这里将其改成盒子滤波场景,去掉了Bias),对于代码中的细节都在注释里面详细的描述,这里的计算是十分巧妙的。带详细解析版的代码如下,介于篇幅原因这里只贴出完整代码中核心部分的内联汇编实现,完整实现请移步我的github地址:https://github.com/BBuf/ArmNeonOptimization ,如果内容对你有用请点个星哦。
//q9->[d18, d19]
//q10->[d20, 0]
//neon assembly
// : "0"(nn),
// "1"(outptr),
// "2"(outptr2),
// "3"(r0),
// "4"(r1),
// "5"(r2),
// "6"(r3),
// "w"(k012), // %14
// "w"(k345), // %15
// "w"(k678) // %16
if(nn > 0){
asm volatile(
"pld [%3, #192] \n"
// 因为每一行连续计算 4 个输出,所以连续加载
// 6个数据即可,4个窗口移动步长为1,有重叠
// r0 原来的内存排布 [a, b, c, d, e, f]
// d18 -> [a, b], r19 -> [c, d], r20 -> [e, f]
"vld1.f32 {d18-d20}, [%3 :64] \n" //r0
// r0 指针移动到下一次读取起始位置也就是 e
"add %3, #16 \n"
// q9 = [d18, d19] = [a, b, c, d]
// q10 = [d20, d21] = [e, f, *, *]
// q11 = [b, c, d, e]
// q12 = [c, d, e, f]
// 关于 vext 见:https://community.arm.com/developer/ip-products/processors/b/processors-ip-blog/posts/coding-for-neon---part-5-rearranging-vectors
//
"vext.32 q11, q9, q10, #1 \n"
"vext.32 q12, q9, q10, #2 \n"
"0: \n"
// 这里计算有点巧妙
// 首先因为4个卷积窗口之间是部分重叠的
// q9 其实可以看做是4个连续窗口的第1个元素排在一起
// q11 可以看做是4个连续窗口的第2个元素排在一起
// q12 可以看做是4个连续窗口的第3个元素排在一起
// 原来连续4个卷积窗口对应的数据是
// [a, b, c], [b, c, d], [c, d, e], [d, e, f]
// 现在相当于 是数据做了下重排,但是重排的方式很巧妙
// q9 = [a, b, c, d]
// q11 = [b, c, d, e]
// q12 = [c, d, e, f]
// 然后下面的代码就很直观了,q9 和 k012 权值第1个权值相乘
// 因为 4 个窗口的第1个元素就只和 k012 第1个权值相乘
// %14 指 k012,假设 %14 放 q0 寄存器,%e 表示取 d0, %f指取 d1
"vmul.f32 q7, q9, %e14[0] \n" //
// 4 个窗口的第2个元素就只和 k012 第2个权值相乘
"vmul.f32 q6, q11, %e14[1] \n" //
// 4 个窗口的第3个元素就只和 k012 第3个权值相乘
// 这样子窗口之间的计算结果就可以直接累加
// 然后q13相当于只算了3x3卷积第一行 1x3 卷积,中间结果
// 下面指令是把剩下 的 两行计算完
"vmul.f32 q13, q12, %f14[0] \n"
// 计算第二行
"pld [%4, #192] \n"
"vld1.f32 {d18-d20}, [%4] \n" // r1
"add %4, #16 \n"
//把第二行的[a, b, c, d] 和 k345 的第1个权值相乘,然后累加到q7寄存器上
"vmla.f32 q7, q9, %e15[0] \n"
"vext.32 q11, q9, q10, #1 \n"
"vext.32 q12, q9, q10, #2 \n"
//把第二行的[b, c, d, e] 和 k345 的第2个权值相乘,然后累加到q6寄存器上
"vmla.f32 q6, q11, %e15[1] \n"
//把第三行的[c, d, e, f] 和 k345 的第3个权值相乘,然后累加到q13寄存器上
"vmla.f32 q13, q12, %f15[0] \n"
// 为outptr2做准备,计算第二行的 [a, b, c, d, e, f] 和 k012 的乘积
// 把第二行的 [a, b, c, d] 和 k012的第1个权值相乘,赋值给q8寄存器
"vmul.f32 q8, q9, %e14[0] \n"
// 把第二行的 [b, c, d, e] 和 k012的第2个权值相乘,赋值给q14寄存器
"vmul.f32 q14, q11, %e14[1] \n"
// 把第二行的 [c, d, e, f] 和 k012的第3个权值相乘,赋值给q15寄存器
"vmul.f32 q15, q12, %f14[0] \n"
//和上面的过程完全一致,这里是针对第三行
"pld [%5, #192] \n"
"vld1.f32 {d18-d20}, [%5 :64] \n" // r2
"add %5, #16 \n"
// 把第三行的 [a, b, c, d] 和 k678 的第1个权值相乘,然后累加到q7寄存器上
"vmla.f32 q7, q9, %e16[0] \n"
"vext.32 q11, q9, q10, #1 \n"
"vext.32 q12, q9, q10, #2 \n"
// 把第三行的 [b, c, d, e] 和 k678 的第2个权值相乘,然后累加到q6寄存器上
"vmla.f32 q6, q11, %e16[1] \n"
// 把第三行的 [c, d, e, f] 和 k678 的第3个权值相乘,然后累加到q13寄存器上
"vmla.f32 q13, q12, %f16[0] \n"
// 把第三行的 [a, b, c, d] 和 k345 的第1个权值相乘,然后累加到q8寄存器上
"vmla.f32 q8, q9, %e15[0] \n"
// 把第三行的 [b, c, d, e] 和 k345 的第2个权值相乘,然后累加到q14寄存器
"vmla.f32 q14, q11, %e15[1] \n"
// 把第三行的 [c, d, e, f] 和 k345 的第3个权值相乘,然后累加到q15寄存器
"vmla.f32 q15, q12, %f15[0] \n"
"pld [%6, #192] \n"
"vld1.f32 {d18-d20}, [%6] \n" // r3
"add %6, #16 \n"
// 把第四行的 [a, b, c, d] 和 k678 的第1个权值相乘,然后累加到q8寄存器上
"vmla.f32 q8, q9, %e16[0] \n"
"vext.32 q11, q9, q10, #1 \n"
"vext.32 q12, q9, q10, #2 \n"
// 把第四行的 [b, c, d, e] 和 k678 的第2个权值相乘,然后累加到q14寄存器上
"vmla.f32 q14, q11, %e16[1] \n"
// 把第四行的 [c, d, e, f] 和 k678 的第3个权值相乘,然后累加到q15寄存器上
"vmla.f32 q15, q12, %f16[0] \n"
"vadd.f32 q7, q7, q6 \n" // 将q6和q7累加到q7上,针对的是outptr
"pld [%3, #192] \n"
"vld1.f32 {d18-d20}, [%3 :64] \n" // r0
"vadd.f32 q8, q8, q14 \n" // 将q14和q8累加到q8上,针对的是outptr2
"vadd.f32 q7, q7, q13 \n" // 将q13累加到q7上,针对的是outptr
"vadd.f32 q8, q8, q15 \n" // 将q15和q8累加到q8上,针对的是outptr2
"vext.32 q11, q9, q10, #1 \n"
"vext.32 q12, q9, q10, #2 \n"
"add %3, #16 \n"
"vst1.f32 {d14-d15}, [%1]! \n" // 将q7寄存器的值存储到outptr
"vst1.f32 {d16-d17}, [%2]! \n" // 将q8寄存器的值存储到outptr2
"subs %0, #1 \n" // nn -= 1
"bne 0b \n" // 判断条件:nn != 0
"sub %3, #16 \n" //
: "=r"(nn), // %0
"=r"(outptr), // %1
"=r"(outptr2), // %2
"=r"(r0), // %3
"=r"(r1), // %4
"=r"(r2), // %5
"=r"(r3) // %6
: "0"(nn),
"1"(outptr),
"2"(outptr2),
"3"(r0),
"4"(r1),
"5"(r2),
"6"(r3),
"w"(k012), // %14
"w"(k345), // %15
"w"(k678) // %16
: "cc", "memory", "q6", "q7", "q8", "q9", "q10", "q11", "q12", "q13", "q14", "q15"
);
}
同样打印一下盒子滤波的输出矩阵的前20个元素:
308.00000 343.00000 360.00000 352.00000 330.00000 318.00000 327.00000 338.00000 331.00000 314.00000 304.00000 307.00000 323.00000 341.00000 348.00000 348.00000 350.00000 355.00000 355.00000 353.00000
和前面的两个版本是一致的,证明代码改写无误,然后耗时情况可以从第一节的图中看到,由236.82ms变成 68.54ms,接近4倍的加速,并且比我一份朴实无华的移动端盒子滤波算法优化笔记中最快的版本还快2-3倍。
5. Neon AssemblyV2
因为我们是盒子滤波,然后卷积核全部为1,实际上乘法对我们来说就不是必要的了,所以我们可以去掉所有的乘法相关的指令,改用vadd来实现相关操作。这样可以对上个版本进行进一步加速,将上一节的核心代码利用vadd指令改写后的代码如下::
//注意这个过程是计算盒子滤波,所以不会像NCNN一样考虑Bias
for (; i + 1 < OutHeight; i += 2){
// 在循环体内每行同时计算4个输出
// 同时计算两行,也就是一次输出 2x4 个点
int nn = OutWidth >> 2;
int remain = OutWidth - (nn << 2);
//q9->[d18, d19]
//q10->[d20, 0]
//neon assembly
// : "0"(nn),
// "1"(outptr),
// "2"(outptr2),
// "3"(r0),
// "4"(r1),
// "5"(r2),
// "6"(r3),
// "w"(k012), // %14
// "w"(k345), // %15
// "w"(k678) // %16
if(nn > 0){
asm volatile(
"pld [%3, #192] \n"
// 因为每一行连续计算 4 个输出,所以连续加载
// 6个数据即可,4个窗口移动步长为1,有重叠
// r0 原来的内存排布 [a, b, c, d, e, f]
// d18 -> [a, b], r19 -> [c, d], r20 -> [e, f]
"vld1.f32 {d18-d20}, [%3 :64] \n" //r0
"add %3, #16 \n"
"vext.32 q11, q9, q10, #1 \n"
"vext.32 q12, q9, q10, #2 \n"
"0: \n"
"vmov.f32 q7, q9 \n" //
"vmov.f32 q6, q11 \n" //
"vmov.f32 q13, q12 \n"
"pld [%4, #192] \n"
"vld1.f32 {d18-d20}, [%4] \n" // r1
"add %4, #16 \n"
"vadd.f32 q7, q7, q9 \n"
"vext.32 q11, q9, q10, #1 \n"
"vext.32 q12, q9, q10, #2 \n"
"vadd.f32 q6, q11, q6 \n"
"vadd.f32 q13, q12, q13 \n"
"vmov.f32 q8, q9 \n"
"vmov.f32 q14, q11 \n"
"vmov.f32 q15, q12 \n"
"pld [%5, #192] \n"
"vld1.f32 {d18-d20}, [%5 :64] \n" // r2
"add %5, #16 \n"
"vadd.f32 q7, q9, q7 \n"
"vext.32 q11, q9, q10, #1 \n"
"vext.32 q12, q9, q10, #2 \n"
"vadd.f32 q6, q11, q6 \n"
"vadd.f32 q13, q12, q13 \n"
"vmov.f32 q8, q9 \n"
"vmov.f32 q14, q11 \n"
"vmov.f32 q15, q12 \n"
"pld [%6, #192] \n"
"vld1.f32 {d18-d20}, [%6] \n" // r3
"add %6, #16 \n"
"vmov.f32 q8, q9 \n"
"vext.32 q11, q9, q10, #1 \n"
"vext.32 q12, q9, q10, #2 \n"
"vmov.f32 q14, q11 \n"
"vmov.f32 q15, q12 \n"
"vadd.f32 q7, q7, q6 \n"
"pld [%3, #192] \n"
"vld1.f32 {d18-d20}, [%3 :64] \n" // r0
"vadd.f32 q8, q8, q14 \n" // 将q14和q8累加到q8上,针对的是outptr2
"vadd.f32 q7, q7, q13 \n" // 将q13累加到q7上,针对的是outptr
"vadd.f32 q8, q8, q15 \n" // 将q15和q8累加到q8上,针对的是outptr2
"vext.32 q11, q9, q10, #1 \n"
"vext.32 q12, q9, q10, #2 \n"
"add %3, #16 \n"
"vst1.f32 {d14-d15}, [%1]! \n" // 将q7寄存器的值存储到outptr
"vst1.f32 {d16-d17}, [%2]! \n" // 将q8寄存器的值存储到outptr2
"subs %0, #1 \n" // nn -= 1
"bne 0b \n" // 判断条件:nn != 0
"sub %3, #16 \n" //
: "=r"(nn), // %0
"=r"(outptr), // %1
"=r"(outptr2), // %2
"=r"(r0), // %3
"=r"(r1), // %4
"=r"(r2), // %5
"=r"(r3) // %6
: "0"(nn),
"1"(outptr),
"2"(outptr2),
"3"(r0),
"4"(r1),
"5"(r2),
"6"(r3),
"w"(k012), // %14
"w"(k345), // %15
"w"(k678) // %16
: "cc", "memory", "q6", "q7", "q8", "q9", "q10", "q11", "q12", "q13", "q14", "q15"
);
}
这里的代码注释和上一节基本一样,介于文章长度这里就删除掉了,可以结合上一小节的代码注释理解。
最后打印输出矩阵的前20个元素如下:
308.00000 343.00000 360.00000 352.00000 330.00000 318.00000 327.00000 338.00000 331.00000 314.00000 304.00000 307.00000 323.00000 341.00000 348.00000 348.00000 350.00000 355.00000 355.00000 353.00000
和之前的版本也完全一致,说明这个指令集改写应该是无误的,然后进行速度测试就获得了第一节图中的最后一列结果了,即从上个版本的68.54ms优化到了61.63ms。
6. 结语
这篇文章主要是对NCNN 的3x3可分离卷积的armv7架构的实现进行了非常详细的解析和理解,然后将其应用于 3 × 3 3\times 3 3×3盒子滤波,并获得了最近关于盒子滤波的优化实验的最快速度(截至到目前,并不代表一定是最快的),希望对做工程部署或者算法优化的读者有一定启发,以上。
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:
![]()
为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新,我们成立了一个QQ群,二维码如下,感兴趣可以加入。
![]()