Java中0.1+0.2问题解释

PS：该帖子答案来自于知乎

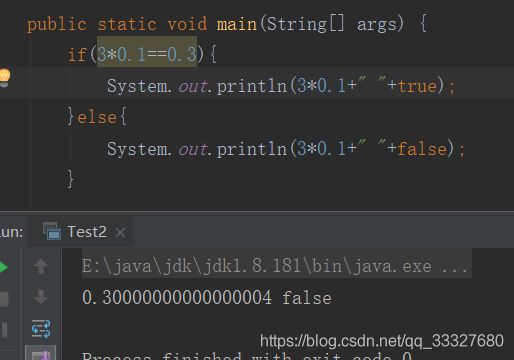
起因：今天遇到一个问题：if（3*0.1==0.3）的结果是true还是false，当时我一看，就说是true，乍一看没毛病，但是面试官告诉我很遗憾，错了，我当时的表情是这样的

这不科学啊，这个问题我曾一度对我的数学老师产生怀疑：莫非当年他教我的都是假的数学？

知道我回家跑了一遍程序才发现

然后我的表情就变成这样了

再然后我问了下万能的度妹，然后找到了知乎上的回答：

 

这个问题不简单，既跟浮点数的表示有关，也跟Java的设计机制有关。

首先参看https://en.wikipedia.org/wiki/IEEE_754-1985了解浮点数是如何表示的。

对于0.1来说，其本质是 1 / 10，那么若你用二进制表示它们，然后除的话，是这样的：1 ／ 1010，然而这一个是除不尽的，是无穷循环。

===> 0.0 00110011001100110011001100110011... 其中0011循环

而根据标准用科学表示法表示的话，就是 x

 

根据这幅图和计算公式 , 我们得到了exponent 是 -4，所以，我们的 e 取值为 1019 （1019 - 1023 = -4），1019的11位二进制表示为0111 1111 011 然后 m，即multipler，为，即1/16。而我们0.1是正数，所以s取值为0。

 

那么根据图就应该这样摆：
0 01111111011 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 (52位）

然后在fraction，部分则为, 那么就应该是 1 / 2 + 1/16 + 1/32 + 1/256 + 1/512 + 1/4096+ 1/8192 + 1/65536 + 1/131072 + 1/1048576 + 1/2097152 + 1/8388608 + ....，约等于0.6，然后再根据标准加上先前的隐式1，大约1.6，然后我们再乘以multipler 1 ／16，值大约是0.10000000000000000555111512312578270211815834045410156。那么，若你在C++当中打印这个值我们也能得到这个结果：

#include 
int main(int argc, char *argv[])
{
  printf("%.53f\n", 0.1);
  return 0;
}

然后若你打印17位的话，就会做round四舍五入，于是会是0.10000000000000001，而这个17位一般是我们计算机浮点数中能表示的区分其它浮点数字的位数，这是最坏的情况，一般来说我们可以更少位数就区分开相邻的浮点数。那么，是不是Java就直接取17位呢？看3 * 0.1似乎是这样，但是4 * 0.1却得到了0.4，若是取17位，应该是0.40000000000000002这样的结果，但是Java是0.4. 这种情况其实也让我疑惑了一下。然后，我去查看了Java println double的源代码，跟踪下去的时候发现println double的时候，是调用这句话

  public static String toString(double d) {
        return FloatingDecimal.toJavaFormatString(d);
 }

然后我去查询java doc: Double (Java Platform SE 7 )

Returns a string representation of the double argument. All characters mentioned below are ASCII characters.

• If the argument is NaN, the result is the string "NaN".
• Otherwise, the result is a string that represents the sign and magnitude (absolute value) of the argument. If the sign is negative, the first character of the result is '-' ('\u002D'); if the sign is positive, no sign character appears in the result. As for the magnitude m:
  • If m is infinity, it is represented by the characters "Infinity"; thus, positive infinity produces the result "Infinity" and negative infinity produces the result "-Infinity".
  • If m is zero, it is represented by the characters "0.0"; thus, negative zero produces the result "-0.0" and positive zero produces the result "0.0".
  • If m is greater than or equal to 10

    -3

    but less than 10 

    7

    , then it is represented as the integer part of m, in decimal form with no leading zeroes, followed by '.' ('\u002E'), followed by one or more decimal digits representing the fractional part of m.
  • If m is less than 10

    -3

    or greater than or equal to 10 

    7

    , then it is represented in so-called "computerized scientific notation." Let n be the unique integer such that 10    

    n

    ≤ m < 10

    n+1

    ; then let a be the mathematically exact quotient of m and 10  

    n

    so that 1 ≤ a < 10. The magnitude is then represented as the integer part of a, as a single decimal digit, followed by '.' ('\u002E'), followed by decimal digits representing the fractional part of a, followed by the letter 'E' ('\u0045'), followed by a representation of n as a decimal integer, as produced by the method Integer.toString(int).

How many digits must be printed for the fractional part of m or a? There must be at least one digit to represent the fractional part, and beyond that as many, but only as many, more digits as are needed to uniquely distinguish the argument value from adjacent values of type double. That is, suppose that x is the exact mathematical value represented by the decimal representation produced by this method for a finite nonzero argumentd. Then d must be the double value nearest to x; or if two double values are equally close to x, then d must be one of them and the least significant bit of the significand of d must be 0.                                                                                              

翻译：返回double参数的字符串表示形式。下面提到的所有字符都是ASCII字符。
如果参数是NaN，则结果是字符串“NaN”。
否则，结果是一个字符串，表示参数的符号和大小（绝对值）。如果符号为负数，则结果的第一个字符为' - '（'\ u002D'）;如果符号为正，则结果中不会出现符号字符。至于幅度m：
如果m是无穷大，则由字符“Infinity”表示;因此，正无穷大产生结果“无穷大”，负无穷大产生结果“无穷大”。
如果m为零，则用字符“0.0”表示;因此，负零产生结果“-0.0”，正零产生结果“0.0”。
如果m大于或等于10
-3
但不到10
7
，然后它表示为m的整数部分，十进制形式，没有前导零，后跟'。' （'\ u002E'），后跟一个或多个十进制数字，表示m的小数部分。
如果m小于10
-3
或大于或等于10
7
然后它以所谓的“计算机化科学记数法”表示。设n是唯一的整数，使得10
ñ
≤m<10
n + 1个
;然后让a成为m和10的数学上精确的商
ñ
因此，1≤a<10。然后，幅度表示为a的整数部分，作为单个十进制数字，后跟'。' （'\ u002E'），后跟表示a的小数部分的十进制数字，后跟字母'E'（'\ u0045'），后跟n表示十进制整数，由Integer方法生成。的toString（INT）。
m或a的小数部分必须打印多少位？必须至少有一个数字来表示小数部分，并且除此之外必须有多个，但只有多少，更多的数字才能唯一地将参数值与double类型的相邻值区分开来。也就是说，假设x是由此方法为有限非零参数生成的十进制表示所表示的精确数学值。那么d必须是最接近x的double值;或者如果两个double值同样接近x，则d必须是其中之一，d的有效位的最低有效位必须为0。

 

以上来自：@蓝色

首先预备知识：
什么是round-trip?
Any double-precision floating-point number can be identified with at most 17 significant decimal digits. This means that if you convert a floating-point number to a decimal string, round it (to nearest) to 17 digits, and then convert that back to floating-point, you will recover the original floating-point number. In other words, the conversion will round-trip.

解释:任何浮点数可以最多被17位十进制数字表示，这意味着如果你转换一个浮点数为十进制字符串需要保留17位数字，这样可以通过这17位数字转换恢复原来的浮点数，这种转换就是round-trip

我们知道了0.1,0.2...0.9，1在计算机保存中的真实值是

但是我们使用Java打印出来的0.1,0.2...0.9，1却是

咋一看，除了0.3打印的很奇怪，精确到小数点后17位，其他好像都是精确到小数点后16位，这就说明 Integer.toString(int)这个方法不是简单的四舍五入，而是所有round-trip字符串中最短的字符串~

为什么0.3不能和真实值round-trip，因为Java不一样，Java在程序中计算出的0.1,0.2...0.9，1是这样的

（ps：可以在Decimal to Floating-Point Converter中验证）
这并不是0.1,0.2...0.9，1的真正转化，这种计算的目的是保留到小数点后一位时仍然可以round-trip，比如0.3可以和0.299999999999999988897769753748434595763683319091796875相互转化，只有0.30000000000000004才能和真实值round-trip。

 

结论：
The floating-point numbers represented by the long strings are printed that way because no shorter strings (e.g., 0.3, 0.8, 0.9, and 1.0) will round-trip.

翻译：
被打印成长字符串的浮点数比如（0.3，0.8，0.9，1.0）是因为打印出的字符串
(如：0.30000000000000004）是满足round-trip字符串中最短的一个、

来自：@罗智勇