【编译原理】第八章 代码优化
第八章 代码优化
8.1 流图
在代码优化之前,需要先分析代码的控制流程,因此需要流图。
流程中每一个基本结点为基本块。
基本块(Basic Block)
基本块是满足下列条件的最大的连续三地址指令序列:
- 控制流只能从基本块的第一个指令进入该块。也就是说,没有跳转到基本块中间或末尾指令的转移指令。
- 除了基本块的最后一个指令,控制流在离开基本块之前不会跳转或者停机。
基本块划分算法
输入:
- 三地址指令序列
输出:
- 输入序列对应的基本块列表,其中每个指令恰好被分配给一个基本块
方法:
- 首先,确定指令序列中哪些指令是首指令(leaders),即某个基本块的第 一个指令
-
- 指令序列的第一个三地址指令是一个首指令
- 任意一个条件或无条件转移指令的目标指令是一个首指令
- 紧跟在一个条件或无条件转移指令之后的指令是一个首指令
-
- 然后,每个首指令对应的基本块包括了从它自己开始,直到下一个首指令(不含)或者指令序列结尾之间的所有指令
例如想下图中一段代码序列和对应基本块:

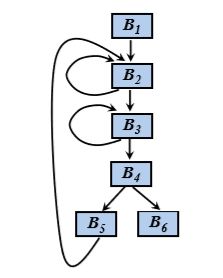
流图(Flow Graphs)
流图的结点是一些基本块 ,从基本块B到基本块C之间有一条边当且仅当基本块C的第一个指令可能紧跟在B的最后一条指令之后执行。
此时称B是C的前驱(predecessor) , C是B的后继(successor)
有两种方式可以确认这样的边:
- 有一个从B的结尾跳转到C的开头的条件或无条件跳 转语句
- 按照原来的三地址语句序列中的顺序,C紧跟在之B 后,且B的结尾不存在无条件跳转语句
8.2 常用代码的优化
本章主要针对机器无关的代码优化。
优化的分类:
机器无关优化
- 针对中间代码
机器相关优化
- 针对目标代码
局部代码优化
- 单个基本块范围内的优化
全局代码优化
- 面向多个基本块的优化
常用的优化方法
- 删除公共子表达式
- 删除无用代码
- 常量合并
- 代码移动
- 强度削弱
- 删除归纳变量
8.2.1 ① 删除公共子表达式
公共子表达式:如果表达式x op y先前已被计算过,并且从先前的计 算到现在,x op y中变量的值没有改变,那么x op y的 这次出现就称为公共子表达式(common subexpression)。
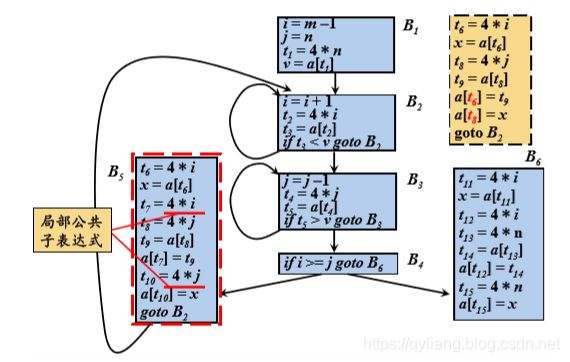
如上调图中的4*i 和4*j 都重复计算了,而中间没有出现i和j值的变化,所以是公共子表达式,需要进行优化,优化后B5变为:
t6 = 4 * i
x = a[t6]
t8 = 4 * j
t9 = a[t8]
a[t6] = t9
a[t8] = x
goto B2
在一个基本块中的代码出现重复称为局部公共子表达式
再进行分析发现表达式前4*i 的值已经被计算过了,而且顺着程序下来这个值并没有改变,所以4*i 为公共子表达式。同理4*j也是公共子表达式。所以t2=t6=4*i,最终用t2表示。
x = a[t2]
t9 = a[t4]
a[t2] = t9
a[t4] = x
goto B2
跨越了基本块都没有改变的称为全局公共子表达式
再分析发现 a[t2] 被计算过,a[t4] 也被计算过,所以x = t3, a[t2] = t5 ,最终B5可以表示为:
x = t3
a[t2] = t5
a[t4] = x
goto B2
分析B6也是可以简化的:
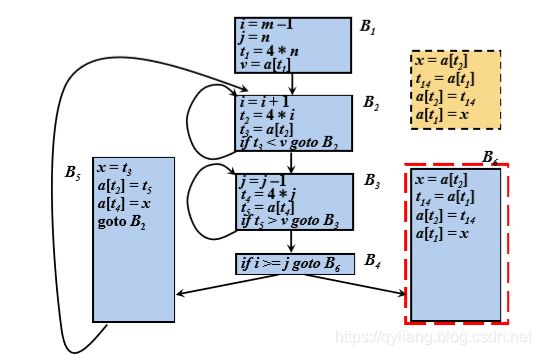
初步简化之后,发现 a[t2] 和a[t1] 也为公共子表达式,a[t2]可以换成t3,因为他和上面B2的t3相等,不管程序是否进入过B5,但只要进入B6,那里的a[t2]就和t3相等。
而a[t1]设计到B1,此时程序可能进入B5分支,也可能进入B6分支,如果替换a[t1]将会是不稳妥的。
虽然a[t2]涉及到分支,但分支在内部,就算B5改变了a[t2],那么改变后的也会传递到B6,;而B1在分支外部,B5的改变不会传递到B1,所以B6中的a[t1]可能无法感知到变化。
关键问题: 计算机如何自动识别公共子表达式
8.2.2 ②删除无用代码
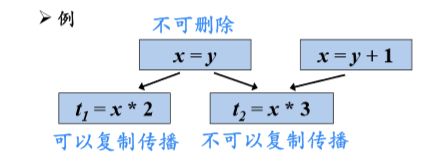
复制传播指常用的公共子表达式消除算法和其它一些优化算法会引入 一些复制语句(形如x = y的赋值语句)。
复制传播:在复制语句x = y之后尽可能地用y代替x
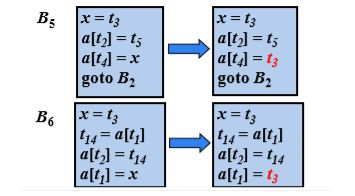
这样就可以删除x=t3的代码了。复制传播给删除无用代码带来机会。
无用代码(死代码Dead-Code ) :其计算结果永远不会被使用的语句。
关键问题是:如何自动识别无用代码。
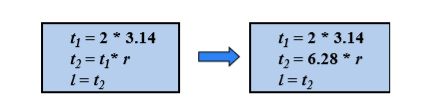
8.2.3 ③ 常量合并(Constant Folding)
如果在编译时刻推导出一个表达式的值是常量,就可以 使用该常量来替代这个表达式。该技术被称为常量合并
8.2.4 ④ 代码移动(Code Motion)
这个转换处理的是那些不管循环执行多少次都得到相同结果的表达式(即循环不变计算,loop-invariant computation) , 在进入循环之前就对它们求值。
如下列代码:
for( n=10; n<360; n++ )
{
S=1/360*pi*r*r*n;
printf( “Area is %f ”, S );
}
可以改为:
C= 1/360*pi*r*r;
for( n=10; n<360; n++ )
{
S=C*n;
printf( “Area is %f ”, S );
}
关键问题:如何自动识别循环不变计算?
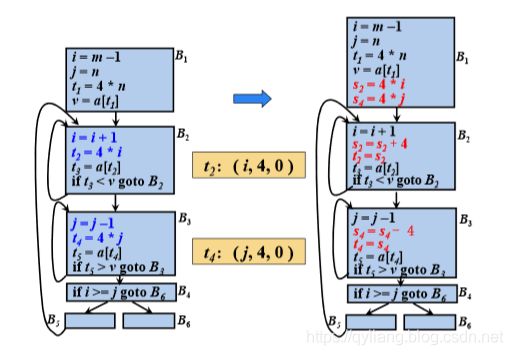
8.2.5 ⑤ 强度削弱(Strength Reduction)
强度削弱指的是用较快的操作代替较慢的操作,如用加代替乘。
归纳变量 :对于一个变量x ,如果存在一个正的或负的常数c使得每次x被赋值时它的值总增加c ,那么x就称为归纳 变量(Induction Variable)
归纳变量可以通过在每次循 环迭代中进行一次简单的增量运算(加法或减法)来计算:
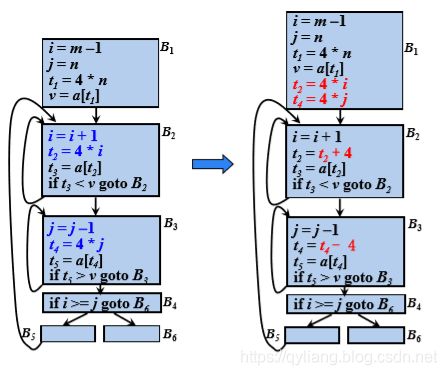
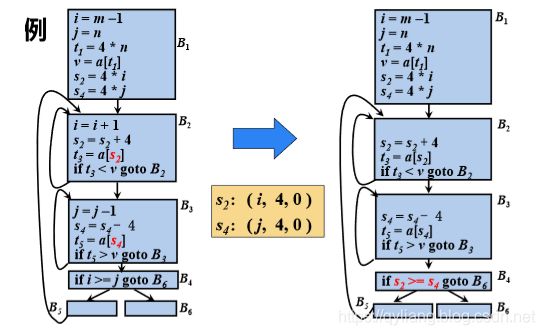
8.2.6 ⑥ 删除归纳变量
在沿着循环运行时,如果有 一组归纳变量的值的变化保持步调一致,常常可以将这 组变量删除为只剩一个
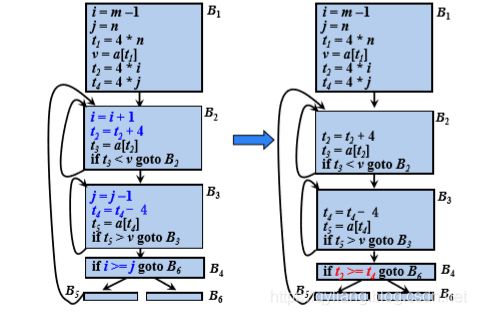
8.3 基本块的优化
基本块的优化也局部优化,基本块的优化针对每个基本块内部。
很多重要的局部优化技术首先把一个基本块转换成为 一个**无环有向图(directed acyclic graph, DAG) **
基本块的 DAG 表示
例
a = b + c
b = a - d
c = b + c
d = a - d
基本块中的每个语句s都对应一个内部结点N :
- 结点N的标号是s中的运算符;同时还有一个定值变量表被关联到N ,表示s是在此基本块内最晚对表中变量进行定值的语句。
- N的子结点是基本块中在s之前、最后一个对s所使用的运算分量进行定值的语句对应的结点。如果s的某个运算分量在基本块内没有在s之前被定值,则这个运算分量对应的子结点就是代表该运算分量初始值的叶结点(为区别起见, 叶节点的定值变量表中的变量加上下脚标0) 。
- 在为语句x=y+z构造结点N的时候,如果x已经在某结点M的定值变量表中,则从M的定值变量表中删除变量x。
对于形如x=y+z的三地址指令, 如果已经有一个结点表示y+z, 就不往DAG中增加新的结点, 而是给已经存在的结点附加定值变量x
上述程序中的DAG图如下所示:

基于基本块的 DAG 删除无用代码
从一个DAG上删除所有没有附加活跃变量(活跃变量是指其值可能会在以后被使用的变量)的根结点(即没有父 结点的结点) 。重复应用这样的处理过程就可以从DAG 中消除所有对应于无用代码的结点
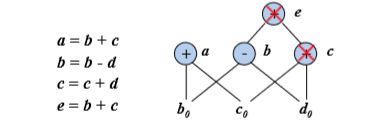
假设a和b是活跃变量,但c和e不是。
根据基本块的DAG可以获得一些非常有用的信息
确定哪些变量的值在该基本块中赋值前被引用过 :在DAG中创建了叶结点的那些变量 。
确定哪些语句计算的值可以在基本块外被引用 :在DAG构造过程中为语句s(该语句为变量x定值)创建的节点N,在DAG构造结束时x仍然是N的定值变量。
对每个具有若干定值变量的节点,构造一个三地址语句来计算其中某个变量的值 ,倾向于把计算得到的结果赋给一个在基本块出口处活跃的变 量(如果没有全局活跃变量的信息作为依据,就要假设所有变 量都在基本块出口处活跃,但是不包含编译器为处理表达式 而生成的临时变量) 。如果结点有多个附加的活跃变量,就必须引入复制语句, 以便给每一个变量都赋予正确的值。
举例:
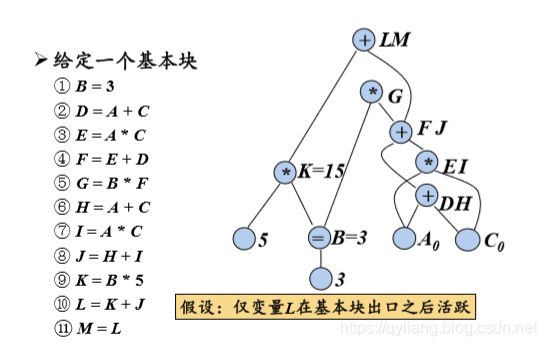
可以删除没有附加活跃变量的根节点M和G,删除冗余的J、I、H变量,并将B直接用3替代,K用15替代。最终11行代码可以简化为一下4句代码:
D = A + C
E = A * C
F = E + D
L = 15 + F
8.4 数据流分析
大部分全局优化都是基于数据流分析实现的,数据流分析是一组用来获取程序执行路径上的数据流信息的技术 ,其应用包括了:
- 到达-定值分析(Reaching-Definition Analysis)
- 活跃变量分析(Live-Variable Analysis)
- 可用表达式分析(Available-Expression Analysis)
在每一种数据流分析应用中,都会把每个程序点和 一个数据流值关联起来。
**语句的数据流模式 **
IN[s]:语句s之前的数据流值 -
OUT[s]:语句s之后的数据流值
f s f_s fs:语句s的传递函数(transfer function) :表示一个赋值语句s之前和之后的数据流值的关系
- 传递函数的两种风格
- 信息沿执行路径前向传播(前向数据流问题) : O U T [ s ] = f s ( I N [ s ] ) OUT[s] = f_s (IN[s]) OUT[s]=fs(IN[s])
- 信息沿执行路径逆向传播(逆向数据流问题) : I N [ s ] = f s ( O U T [ s ] ) IN[s]= f_s (OUT[s]) IN[s]=fs(OUT[s])
基本块中相邻两个语句之间的数据流值的关系 : I N [ s i + 1 ] = O U T [ s i ] i = 1 , 2 , … , n − 1 IN[s_{i+1}]= OUT[s_i] i=1, 2, … , n-1 IN[si+1]=OUT[si]i=1,2,…,n−1
即前一个语句的输出为后一个语句的输入。
基本块上的数据流模式
IN[B]:紧靠基本块B之前的数据流值
OUT[B]: 紧随基本块B之后的数据流值
设基本块B由语句s1,s2,…,sn顺序组成,则
- IN[B] = IN[s1]
- OUT[B] = OUT[sn]
fB:基本块B的传递函数 :
- 前向数据流问题:OUT[B]= fB(IN[B]) ,fB= fsn·…·fs2 ·fs1
- 逆向数据流问题:IN[B]= fB(OUT[B]) ,fB= fs1·fs2 · …·fsn
OUT[B]
= OUT[sn]
= fsn(IN[sn])
= fsn(OUT[sn-1])
= fsn·fs(n-1)(IN[sn-1])
= fsn·fs(n-1)(OUT[sn-2]) ……
= fsn·fs(n-1)·…·fs2(OUT[s1])
= fsn·fs(n-1)·…·fs2·fs1(IN[s1])
=fsn·fs(n-1)·…·fs2·fs1 (IN[B])
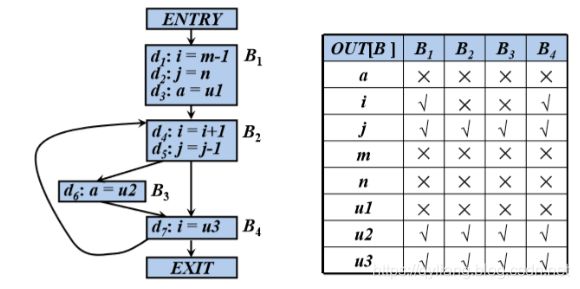
8.4.1 到达定值分析
定值(Definition):变量x的定值是(可能)将一个值赋给x的语句
到达定值(Reaching Definition) :如果存在一条从紧跟在定值d后面的点到达某一程序点p的路径, 而且在此路径上d没有被“杀死”(如果在此路径上有对变量x 的其它定值d′,则称变量x被这个定值d′“杀死”了) ,**则称定值d到达程序点p **
直观地讲,如果某个变量x的一个定值d到达点p,在点p处使用的x的值可能就是由d最后赋予的。
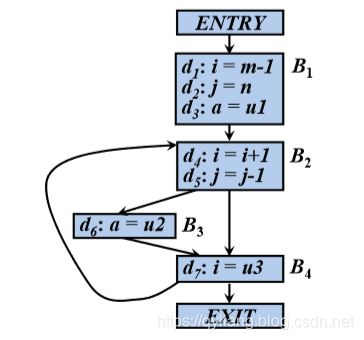
假设每个控制流图都有两个空基本块, 分别是表示流图的开始点的ENTRY结 点和结束点的EXIT结点(所有离开该 图的控制流都流向它)
则定值分析的结果为:
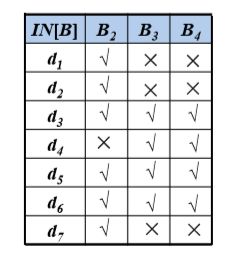
如d1,d2,d3都可以到达B2,d4不行,因为d4必须经过B4,而B4对i有修改,所以不能到达。
到达定值分析的主要用途
- 循环不变计算的检测
- 如果循环中含有赋值x=y+z,而y和z所有可能的定值都在循环 外面(包括y或z是常数的特殊情况) ,那么y+z就是循环不变计算
- 常量合并
- 如果对变量x的某次使用只有一个定值可以到达,并且该定值把一个常量赋给x ,那么可以简单地把x替换为该常量
- 判定变量x在p点上是否未经定值就被引用
“生成”与“杀死”定值
定值d: u= v+ w
该语句“生成”了一个对变量u的定值d,并“杀死” 了程序中其它对u的定值
到达定值的传递函数
f d f_d fd:定值d: u = v + w的传递函数
f ( x ) = g e n d ∪ ( x − k i l l d ) f_ (x) = gen_d ∪(x-kill_d ) f(x)=gend∪(x−killd)
f B f_B fB:基本块B的传递函数
f B ( x ) = g e n B ∪ ( x − k i l l B ) f_B (x) = gen_B ∪(x-kill_B ) fB(x)=genB∪(x−killB)
k i l l B = k i l l 1 ∪ k i l l 2 ∪ … ∪ k i l l n kill_B=kill_1 ∪kill_2 ∪… ∪kill_n killB=kill1∪kill2∪…∪killn,被基本块B中各个语句杀死的定值的集合
g e n B = g e n n ∪ ( g e n n − 1 – k i l l n ) ∪ ( g e n n − 2 – k i l l n − 1 – k i l l n ) ∪ … ∪ ( g e n 1 – k i l l 2 – k i l l 3 – … – k i l l n ) gen_B = genn ∪(gen_n-1 –kill_n ) ∪(gen_{n-2 }–kill_{n-1} –kill_n ) ∪… ∪ (gen_1 –kill_2 –kill_3 –…–kill_n ) genB=genn∪(genn−1–killn)∪(genn−2–killn−1–killn)∪…∪(gen1–kill2–kill3–…–killn)
基本块中没有被块中各语句“杀死”的定值的集合
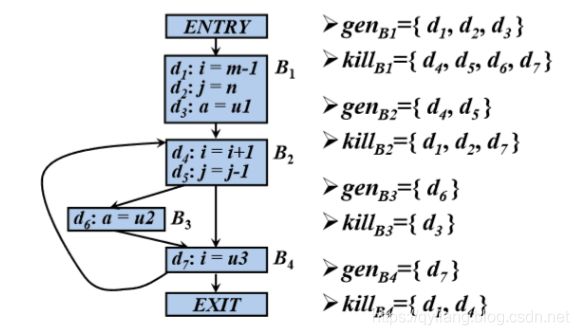
IN[B]:到达流图中基本块B的入口处的定值的集合
OUT[B]:到达流图中基本块B的出口处的定值的集合
方程 :
OUT[ENRTY]=Φ
OUT[B] = genB∪(IN[B]-killB)
O U T [ B ] = f B ( I N [ B ] ) ( B ≠ E N T R Y ) OUT[B]=f_B(IN[B])( B≠ENTRY) OUT[B]=fB(IN[B])(B̸=ENTRY)
f B ( x ) = g e n B ∪ ( x − k i l l B ) f_B(x) = gen_B∪(x-kill_B) fB(x)=genB∪(x−killB)
IN[B]= ∪P是B的一个前驱OUT[P] ( B≠ENTRY)
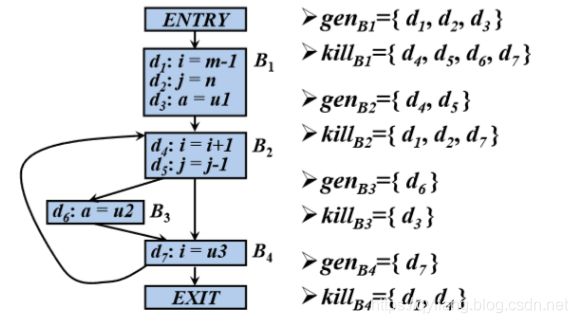
genB和killB的值可以直接从流图计算出来, 因此在方程中作为已知量
输入:流图G,其中每个基本块B的genB和killB都已计算出来
输出: IN[B]和OUT[B]
方法:
OUT[ENTRY] = Φ;
for (除ENTRY之外的每个基本块B) OUT[B] = Φ;
while (某个OUT值发生了改变)
for (除ENTRY之外的每个基本块B)
{
IN[B]= ∪P是B的一个前驱OUT[P];
OUT[B] = genB∪(IN[B]-killB)
}
迭代的过程如下:
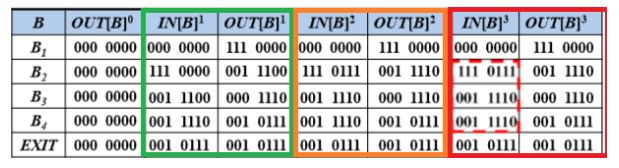
I N [ B ] 1 , O U T [ B ] 1 IN[B]^1,OUT[B]^1 IN[B]1,OUT[B]1表示第一次迭代,用绿色表示,
首先B1的IN为000 0000,B1的OUT为111 0000,表示b1,b2,b3进入B1;
B2的IN为111 000,OUT为001 1100因为B2杀死了d1,d2,生成了d4,d5;
B3的IN为001 1100,OUT为000 1110,因为B3杀死了d3,生成了d6;
B4的IN为001 1110,因为B4的前驱还有B2,所以IN[B4]包括了没有被B3杀死的d3,OUT为001 0111,因为B4杀死了d4,生成了d7。
I N [ B ] 2 , O U T [ B ] 2 IN[B]^2,OUT[B]^2 IN[B]2,OUT[B]2表示第二次迭代,用橙色表示,
B1保持不变
B2的IN值为B1和B4中OUT值得并集,即111 0111,B2的OUT值中先杀死了d1,d2,d7,然后生成了d4,d5,所以为001 1110;
B3的IN值为B2的OUT值001 1110,B3的OUT值中先杀死了d3,然后生成了d6,最终为000 1110;
B4的IN值为B2和B3OUT值得并集,为001 1110,B4的OUT值中先杀死了d1,d4,然,后生成了d7,最终为001 0111;
一直迭代至OUT不发生变化的时候结束。再迭代一次发现不再改变
最终结果和人工分析出来的结果相同:

引用-定值链(Use-Definition Chains)
引用-定值链(简称ud链)是一个列表,对于变量的每一次引 用,到达该引用的所有定值都在该列表中
- 如果块B中变量a的引用之前有a的定值, 那么只有a的最后一次定值会在该引用的 ud链中
- 如果块B中变量a的引用之前没有a的定值, 那么a的这次引用的ud链就是IN[B]中a的 定值的集合
8.4.2 活跃变量分析
活跃变量
对于变量x和程序点p,如果在流图中沿着从p开始的某条路径会引用变量x在p点的值,则称变量x在点p是活跃(live)的,否则称变量x在点p不活跃(dead)。
例:各基本块的出口处的活跃变量
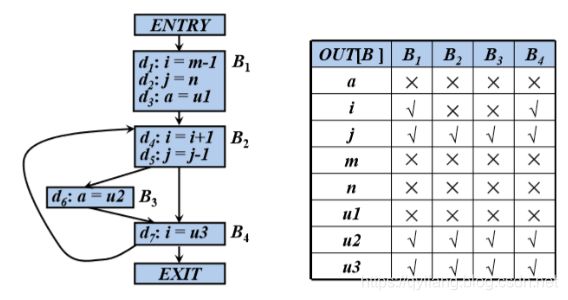
对a而言,没有基本块对a的值进行引用,所以在各个基本块中是不活跃的。
重点是有没有引用a的值,而对a的重新赋值并不能算是引用a原来的值。
对i而言,i在B1的出口处得到了B2的引用,所以在B1中是活跃的。从B4出来的i在B2中得到了引用,所以在B4处是活跃的。
被引用了,要看是从哪个程序点p出来的,则就是p处的活跃变量。
对j而言,首先在B1处活跃,而B2的循环路径中,没有对j的重新定值,但j被B2引用,所以j在B2,B3,B4中都是活跃的。
相对于i而言,它在循环中被重新定值了,所以只有在B4中是活跃的。简而言之,j在循环中不能“死”。
对m,n,u1而言,没有对他们的引用,所以不是活跃的。(冗余变量)
对u2而言,从各个基本块离开以后,都可以进入B3中,而B3中对u2引用且没有重新定值,所以都是活跃的。
活跃变量信息的主要用途
删除无用赋值
- 无用赋值:如果x在点p的定值在基本块内所有后继点都不被引用,且x在基本块出口之后又是不活跃的,那么x在点p的定值就 是无用的
为基本块分配寄存器
- 如果所有寄存器都被占用,并且还需要申请一个寄存器,则应该考虑使用已经存放了死亡值的寄存器,因为这个值不需要保 存到内存
- 如果一个值在基本块结尾处是死的就不必在结尾处保存这个值
活跃变量的传递函数
逆向数据流问题: I N [ B ] = f B ( O U T [ B ] ) IN[B]= f_B(OUT [B]) IN[B]=fB(OUT[B])
f B ( x ) = u s e B ∪ ( x − d e f B ) f_B (x) = use_B ∪(x-def_B ) fB(x)=useB∪(x−defB)
- d e f B def_B defB :在基本块B中定值,但是定值前在B中没有被引用的变量的集
- u s e B use_B useB :在基本块B中引用,但是引用前在B中没有被定值的变量集合
例如:各基本块B的useB 和defB
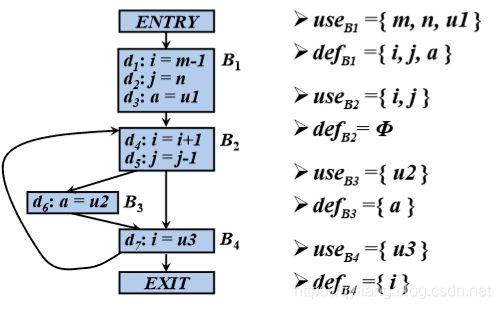
IN[B]:在基本块B的入口处的活跃变量集合
OUT[B]:在基本块B的出口处的活跃变量集合
方程 :
I N [ B ] = f B ( O U T [ B ] ) ( B ≠ E X I T ) IN[B] = f_B(OUT[B])( B≠EXIT) IN[B]=fB(OUT[B])(B̸=EXIT)
f B ( x ) = u s e B ∪ ( x − d e f B ) f_B(x) = use_B∪(x-def_B) fB(x)=useB∪(x−defB)
所以:
I N [ B ] = u s e B ∪ ( O U T [ B ] − d e f B ) IN[B] = use_B∪(OUT[B]-def_B) IN[B]=useB∪(OUT[B]−defB)
入口处活跃的变量为当前使用的,并上出口处活跃的减去定义的。
O U T [ B ] = ∪ S 是 B 的 一 个 后 继 I N [ S ] ( B ≠ E X I T ) OUT[B]= ∪_{S是B的一个后继}IN[S] ( B≠EXIT) OUT[B]=∪S是B的一个后继IN[S](B̸=EXIT)
出口处活跃的变量,为每一个后继入口处活跃的变量的集合。
计算活跃变量的迭代算法
输入:流图G,其中每个基本块B的useB 和defB都已计算出来
输出:IN[B]和OUT[B]
方法:
IN[EXIT] = Φ;
for(除EXIT之外的每个基本块B) IN[B] = Φ;
while(某个IN值发生了改变)
for(除EXIT之外的每个基本块B)
{
OUT[B] = ∪S是B的一个后继IN[S];
IN[B] = useB∪(OUT[B] -defB);
}
对下图的迭代分析结果如图所示:
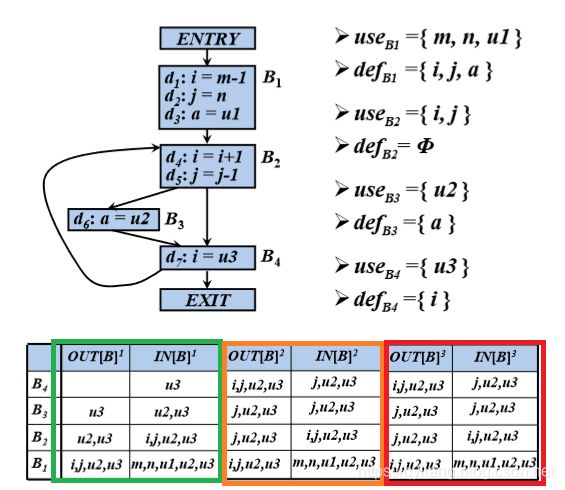
活跃变量的分析时逆向数据流分析,所以是沿着反方向计算的。
第一次迭代中:
B4中OUT为空,IN值为u3;
B3中OUT为B4的IN值,为u3,IN值为u2+(u3-a)=u2,u3;
B2中的OUT值为B3和B4中的IN值,为u2、u3,B2的IN值为i,j+({u2,u3})=i,j,u2,u3。
B1中的OUT值为B2中的IN值,为i,j,u2,u3,IN值为m,n,u1+({i,j,u2,u3}-{i,j,a})=m,n,u1,u2,u3。
第二次迭代中:
B4中OUT为B2的IN值i,j,u2,u3,IN值为u3+({i,j,u2,u3}-i)=j,u2,u3;
B3中OUT为B4的IN值j,u2,u3,IN值为u2+({j,u2,u3}-a)=j,u2,u3
B2中的OUT值为B3和B4中的IN值j,u2,u3,IN值为i,j+({j,u2,u3})=i,j,u2,u3
B1中的OUT值为B2中的IN值i,j,u2,u3,IN值为m,n,u1+({i,j,u2,u3}-{i,j,a})=m,n,u1,u2,u3。
再迭代一次发现IN值不再变化。
定值-引用链:设变量x有一个定值d,该定值所有能够到达的引 用u的集合称为x在d处的定值-引用链,简称du。
如果在求解活跃变量数据流方程中的OUT[B]时,将OUT[B]表示 成从B的末尾处能够到达的引用的集合,那么,可以直接利用这 些信息计算基本块B中每个变量x在其定值处的du链
- 如果B中x的定值d之后有x的第一个定值d′, 则d和d′之间x的所有引用构成d的du链
- 如果B中x的定值d之后没有x的新的定值, 则B中d之后x的所有引用以及OUT[B]中x的 所有引用构成d的du链
8.4.3 可用表达式分析
可用表达式,即可以直接使用的表达式,不需要在设置一个重复的表达式。
如果从流图的首节点到达程序点p的每条路径都对表达式x op y进行计算,并且从最后一个这样的计算到点p之间没有再次对x或y定值,那么表达式x op y在点p是可用的(available)。
在点p上,x op y已经在之前被计算过,不需要重新计算
可用表达式的传递函数
对于可用表达式数据流模式而言,如果基本块B对x或者y进行了 (或可能进行)定值,且以后没有重新计算x op y,则称B杀死表达 式x op y。如果基本块B对x op y进行计算,并且之后没有重新定值x或y,则称B生成表达式x op y.
f B ( x ) = e _ g e n B ∪ ( x − e _ k i l l B ) f_B(x)= e\_gen_B∪(x-e\_kill_B) fB(x)=e_genB∪(x−e_killB)
-
e_genB:基本块B所生成的可用表达式的集合
-
e_killB:基本块B所杀死的U中的可用表达式的集合
U:所有出现在程序中一个或多个语句的右部的表达式的全集
e_genB的计算
初始化:e_genB= Φ
顺序扫描基本块的每个语句:z= xop y
- 把x op y加入e_genB
- 从e_genB中删除和z相关的表达式
上述两步顺序不能颠倒
1.首先为 Φ
2.将{b+c}加入到可用表达式中,并删除所有与a有关的表达式,剩余{b+c}
3.将{a-d}加入到可用表达式中,目前{b+c,a-d},并删除所有与b有关的表达式,剩余{a-d}
4.将{b+c}加入到可用表达式中,目前{a-d,b+c},并删除所有与c有关的表达式,剩余{a-d}
5.将{a-d}加入到可用表达式中,目前{a-d},并删除所有与d有关的表达式,剩余 Φ
e_killB的计算
初始化:e_killB=Φ
顺序扫描基本块的每个语句:z= x op y
- 从e_killB中删除表达式x op y
- 把所有和z相关的表达式加入到e_killB中
可用表达式的数据流方程
IN[B]:在B的入口处可用的U中的表达式集合
OUT[B]:在B的出口处可用的U中的表达式集合
方程:
OUT[ENTRY]= Φ
OUT[B]=fB (IN[B])
fB(x)= e_genB∪(x-e_killB)
I N [ B ] = ∩ P 是 B 的 一 个 前 驱 O U T [ P ] IN[B]= ∩_{P是B的一个前驱}OUT[P] IN[B]=∩P是B的一个前驱OUT[P]
e_genB 和e_killB 的值可以直接从流图计算出来, 因此在方程中作为已知量
计算可用表达式的迭代算法
输入:流图G,其中每个基本块B的e_genB和e_killB都已计算出来
输出:IN[B]和OUT[B]
方法:
OUT[ENTRY] = Φ;
for(除ENTRY之外的每个基本块B) OUT[B] = U;
while(某个OUT值发生了改变)
for (除ENTRY之外的每个基本块B)
{
IN[B]=∩P是B的一个前驱OUT[P]
OUT[B]= e_genB∪(IN[B]-e_killB);
}
为什么将OUT[B]集合初始化为U?
将OUT集合初始化为Φ局限性太大
8.5 内部优化中的循环优化
8.5.1 支配节点和回边
内部优化中的循环优化需要识别支配节点和回边。
如果从流图的入口结点到结点n的每条路径都经过结点d,则称结点d支配(dominate)结点n,记为d dom n 。
每个结点都支配它自己
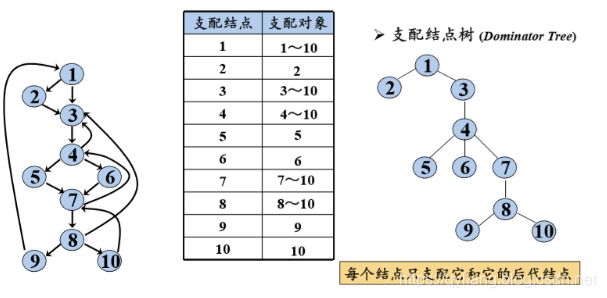
如到达每一个节点都需要经过节点1,所以结点1支配1~10号结点;
继续访问程序可以通过节点2,也可以直接经过结点3,所以结点2支配它自己;
生成的支配结点树如右图所示。
寻找支配结点
支配结点的数据流方程 :
IN[B]:在基本块B入口处的支配结点集合
OUT[B]:在基本块B出口处的支配结点集合
方程:
O U T [ E N T R Y ] = E N T R Y OUT[ENTRY] ={ ENTRY} OUT[ENTRY]=ENTRY
O U T [ B ] = I N [ B ] ∪ B ( B ≠ E N T R Y ) OUT[B] = IN[B]∪{B} ( B≠ENTRY) OUT[B]=IN[B]∪B(B̸=ENTRY)
I N [ B ] = ∩ P 是 B 的 一 个 前 驱 O U T [ P ] ( B ≠ E N T R Y ) IN[B] = ∩_{P是B的一个前驱}OUT[P] ( B≠ENTRY) IN[B]=∩P是B的一个前驱OUT[P](B̸=ENTRY)
计算支配结点的迭代算法
输入:流图G,G的结点集是N,边集是E,入口结点是ENTRY
输出:对于N中的各个结点n,给出D(n),即支配n的所有结点的集合
方法:
OUT[ENTRY]={ENTRY}
for(除ENTRY之外的每个基本块B)
OUT[B]=N
while(某个OUT值发生了改变)
for(除ENTRY之外的每个基本块B)
{
IN[B]=∩P是B的一个前驱OUT[P]
OUT[B]=IN[B]∪{B}
}
例:
回边(Back Edges)
假定流图中存在两个结点d和n满足ddom n。如果存在从结点 n到d的有向边n→d,那么这条边称为回边

8.5.2 自然循环及其识别
有了回边的概念,就可以进行循环的识别了。
从程序分析的角度来看,循环在代码中以什么形式出现并不重要,重要的是它是**否具有易于优化的性质 **
自然循环是满足以下性质的循环 :
- 有唯一的入口结点,称为首结点(header)。首结点支配循环中的所有结点,否则,它就不会成为循环的唯一入口。
- 循环中至少有一条返回首结点的路径,否则,控制就不可能从 “循环”中直接回到循环头,也就无法构成循环
非自然循环的例子:
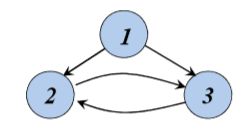
2,3构成一个循环,但它们之间不存在支配关系,所以循环既可以从2进入,也可以从3进入,即入口节点不唯一。
自然循环是一种适合于优化的循环
自然循环的识别:
给定一个回边n → d,该回边的自然循环为:d,以及所有可以不经过d而到达n的结点。d为该循环的首结点。
d支配n
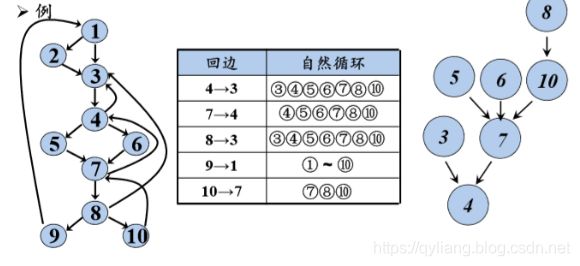
回边4 → 3中,3支配4,除了3以外,7可以到达4,而5,6,10能到达7,8能到达10,所以自然循环包括③④⑤⑥⑦⑧⑩。
自然循环的一个重要性质
除非两个自然循环的首结点相同,否则,它们或者互不相交, 或者一个完全包含(嵌入)在另外一个里面。
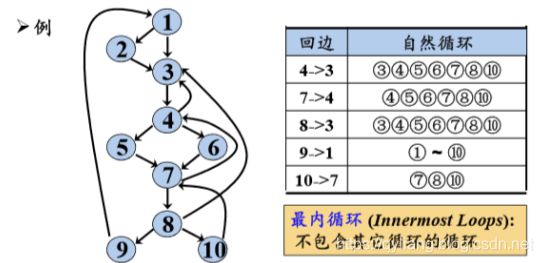
如果两个循环具有相同的首结点,那么很难说哪个是 最内循环。此时把两个循环合并。
8.7 全局优化的具体实现方法
8.7.1 全局公共子表达式和赋值语句的删除
可用表达式的数据流问题可以帮助确定位于流图中p点的表达式是否为**全局公共子表达式 **。

如上图所示,全局公共子表达式x*y可以被删除,删除后复制给u,最终将u传递下来。
具体的算法形式为:
输入:带有可用表达式信息的流图
输出:修正后的流图
方法:
对于语句s:z=xop y,如果xop y在s之前可用,那么执行如下步骤:
- ①从 s开始逆向搜索,但不穿过任何计算了xopy的块,找到所有离 s最近的计算了xop y的语句
- ②建立新的临时变量u
- ③把步骤①中找到的语句w = xop y用下列语句代替: u= x op y ; w= u
- 用z = u替代s
删除复制语句
对于复制语句s:x=y,如果在x的所有引用点都可以用对y的 引用代替对x的引用(复制传播),那么可以删除复制语句x=y
在x的引用点u用y代替x(复制传播)的条件 :复制语句s:x=y在u点“可用”
8.7.2 代码移动
对于循环不变计算,我们可以把它们移到外面去。
代码移动需要做2件事:
- 循环不变计算的检测
- 代码外提
循环不变计算检测算法
输入:循环L,每个三地址指令的ud链
输出:L的循环不变计算语句
方法 :
-
将下面这样的语句标记为“不变”:语句的运算分量或者是常数, 或者其**所有定值点都在循环L外部 **
-
重复执行步骤(3),直到某次没有新的语句可标记为“不变”为止
-
将下面这样的语句标记为“不变”:先前没有被标记过,且所有运算分量或者是常数,或者其所有定值点都在循环L外部,或者只有一 个到达定值,该定值是循环中已经被标记为“不变”的语句。
代码外提
循环不变计算将被移至首结点之前,为此创建一个称为前置 首结点的新块。前置首结点的唯一后继是首结点,并且原来 从循环L外到达L首结点的边都改成进入前置首结点。从循环 L里面到达首结点的边不变
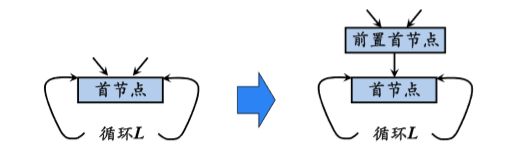
循环不变计算语句s :x = y + z 移动的条件
(1) s所在的基本块是循环所有出口结点(有后继结点在循 环外的结点)的支配结点。
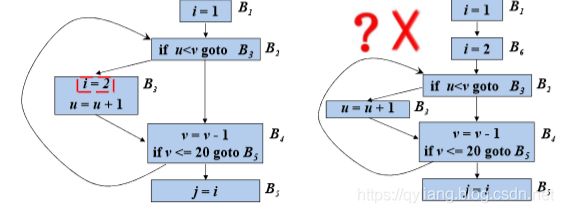
B4是循环出口节点,B3不是B4的支配节点,所以不能移动。
(2) 循环中没有其它语句对x赋值

B2中的i=3不能移动,因为B3中有重新赋值。
(3)循环中对x的引用仅由s到达
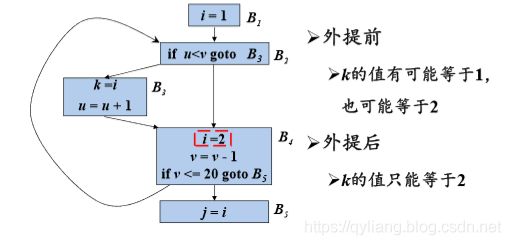
B4中i的引用可以由B1到达,所以不行。
代码移动算法
输入:循环L、ud链、支配结点信息
输出:修改后的循环
方法:
1.寻找循环不变计算
2.对于步骤(1)中找到的每个循环不变计算,检查是否满足上面的**三个条件 **
3.按照循环不变计算找出的次序,把所找到的满足上述条件的循环不 变计算外提到前置首结点中。如果循环不变计算有分量在循环中定值,只有将定值点外提后,该循环不变计算才可以外提。
8.7.3 作用于归纳变量的强度削弱
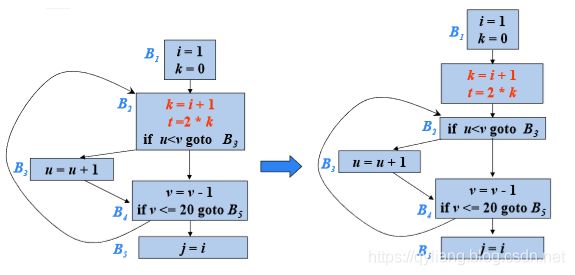
对于一个变量x ,如果存在一个正的或负的常量c ,使得每次 x被赋值时,它的值总是增加c,则称x为归纳变量 。
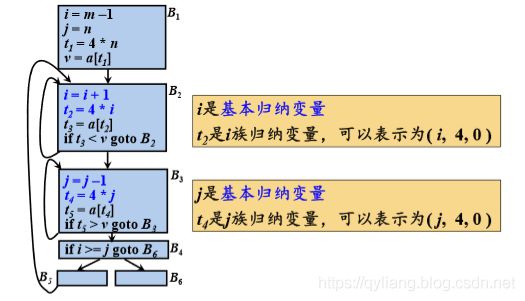
如果循环L中的变量i只有形如i=i+c的定值(c是常量),则称i 为循环L的基本归纳变量 。
如果j = c×i+d,其中i是基本归纳变量,c和d是常量,则j也是 一个归纳变量,称j属于i族 。
基本归纳变量i属于它自己的族
每个归纳变量都关联一个三元组。如果j = c×i+d,其中i是基 本归纳变量,c和d是常量,则与j相关联的三元组是( i, c, d )。
归纳变量检测算法
输入:带有循环不变计算信息和到达定值信息的循环L
输出:一组归纳变量
方法:
-
1.扫描L的语句,找出所有基本归纳变量。在此要用到 循环不变计算信息。与每个基本归纳变量i相关联的 三元组是(i,1, 0)
-
2:寻找L中只有一次定值的变量k,它具有下面的形式:k=c′×j+d′。其中c′和d′是常量,j是基本的或非基本的归纳变量 。
-
如果j是基本归纳变量,那么k属于j族。k对应的三元组可 以通过其定值语句确定
-
如果j不是基本归纳变量,假设其属于i族,k的三元组可 以通过j的三元组和k的定值语句来计算,此时我们还要求:
-
循环L中对j的唯一定值和对k的定值之间没有对i的定值
-
循环L外没有j的定值可以到达k
这两个条件是为了保证对k进行赋值的时候, j当时的值一定等于c*(i当时的值)+d
-
-
-
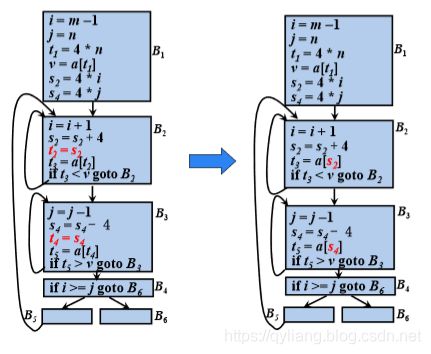
3.在L中紧跟定值i=i+n之后,添加t=t+c*n。将t放入i族,其三元组为(i, c, d)
-
4.在前置节点的末尾,添加语句t=c*i和t=t+d,使得在循环开始的时候 t=c*i+d=j
例如:
8.7.4 归纳变量的删除
对于在强度削弱算法中引入的复制语句j=t,如果在归纳变量j的所有引用点都可以用对t的引用代替对j的引用, 并且j在循环的出口处不活跃,则可以删除复制语句j=t 。
强度削弱后,有些归纳变量的作用只是用于测试。如果 可以用对其它归纳变量的测试代替对这种归纳变量的测 试,那么可以删除这种归纳变量。
删除仅用于测试的归纳变量
对于仅用于测试的基本归纳变量i,取i族的某个归纳变量j (尽量使得c、d简单,即c=1或d=0的情况)。把每个对i的测 试替换成为对j的测试 。
-
( relop i x B )替换为( relop j c*x+d B ),其中x不是归纳变 量,并假设c>0
-
( relop i1 i2 B ),如果能够找到三元组j1 ( i1, c, d )和j2 ( i2, c, d ), 那么可以将其替换为( relop j1 j2 B ) (假设c>0)。否则,测试 的替换可能是没有价值的 。