编译原理--03 语法制导翻译和中间代码生成复习(清华大学出版社第3版)

前言

目录
01 文法和语言、词法分析复习
02 自顶向下、自底向上的LR分析复习
03 语法制导翻译和中间代码生成复习
04 符号表、运行时存储组织和代码优化复习

第7章 语法制导的语义计算

语义分析是上下文有关的，目前较为常见的是用属性文法来描述程序语言语义，并采用语法制导翻译的方法完成对语法成分的翻译工作。

属性文法

属性 描述文法符号的类型、值等有关的一些信息，它可以被计算或传递。

语义动作 指产生式相关联的指定操作

条件谓词 指产生式关联的接受条件，或者根据该条件谓词决定做什么语义动作

语义规则集 通常是产生式关联的一组语义规则，每个语义规则可以是一个语义动作或条件谓词。

属性\(att\)可以与某个文法符号\(a\)关联，用\(a.att\)来表示这种关联

现有一文法：
\(E\rightarrow T_1 + T_2\mid T_1 \&\& T_2\)
\(T\rightarrow num\mid true\mid false\)

将上面的文法描述为类型检查的属性文法：
\(E\rightarrow T_1 + T_2 \quad \{T_1.type=int\quad\&\&\quad T_2.type=int\}\)
\(E\rightarrow T_1 \&\& T_2\quad\{T_1.type=bool\quad\&\&\quad T_2.type=bool\}\)
\(T\rightarrow num\quad\{T.type=int\}\)
\(T\rightarrow true\quad\{T.type=bool\}\)
\(T\rightarrow false\quad\{T.type=bool\}\)

综合属性和继承属性

对关联于产生式\(A\rightarrow \alpha\)的语义动作\(b:=f(c_1, c_2, ..., c_k)\)，如果\(b\)是A的某个属性，则b是A的一个综合属性。综合属性是自底向上传递信息。

对关联于产生式\(A\rightarrow \alpha\)的语义动作\(b:=f(c_1, c_2, ..., c_k)\)，如果\(b\)是产生式右边某个文法符号X的某个属性，则b是A的一个继承属性。继承属性是自顶向下传递信息。

带标注语法分析树，即在语法树的基础上，将原来的非终结符结点修改为综合属性的赋值。

下面是一个简单表达式文法G[S]的一个仅含综合属性的属性文法(开始符号为S)
\(S\rightarrow E\quad\{print(E.val)\}\)
\(E\rightarrow E_1+T\quad\{E.val:=E_1.val+T.val\}\)
\(E\rightarrow T\quad\{E.val:=T.val\}\)
\(T\rightarrow T_1*F\quad\{T.val:=T_1.val\times F.val\}\)
\(T\rightarrow F\quad\{T.val:=F.val\}\)
\(F\rightarrow (E)\quad\{F.val:=E.val\}\)
\(F\rightarrow d\quad\{F.val:=d.lexval\}\)

其中\(d.lexval\)表示数值，\(E.val, T.val, F.val\)都为综合属性
现在要给表达式\(3*(5+4)\)构造语法树和带标注语法分析树：

下面则是一个包含综合属性、继承属性的属性文法：
\(E\rightarrow TR\quad\{R.in:=T.val;\quad E.val:=R.val\}\)
\(R\rightarrow +TR_1\quad\{R_1.in:=R.in+T.val;\quad R.val:=R_1.val\}\)
\(R\rightarrow -TR_1\quad\{R_1.in:=R.in-T.val;\quad R.val:=R_1.val\}\)
\(R\rightarrow \varepsilon\quad\{R.val := R.in\}\)
\(T\rightarrow num\quad\{T.val := lexval(num)\}\)
其中\(lexval(num)\)表示从词法分析程序得到的常数值。
可见\(E.val, T.val, R.val\)都为综合属性，\(R.in\)为继承属性
现在要给表达式\(3+4-5\)构造语法树和带标注语法分析树：

这一章可能的考点

1. 了解综合属性和继承属性。已知属性文法和输入符号串，构建语法树和带标注语法分析树。

第8章 静态语义分析和中间代码生成

中间代码生成

中间代码 一种介于源语言和目标语言的中间语言形式，有：

1. 逆波兰表示
2. 三元式表示
3. 四元式表示
4. 树形表示

逆波兰表示

逆波兰表示法即为后缀表示法，而默认我们使用的表达式是中缀表示法

程序设计语言中的表示	逆波兰表示
\(a+b\)	\(ab+\)
\(-a\)	\(a@\)
\(a+b*c\)	\(abc*+\)
\((a+b)*c\)	\(ab+c*\)
\(a:=b*c+b*d\)	\(abc*bd*+:=\)
\(a:=b*(c+b)*(-d)\)	\(bcb+*d@*:=\)

逆波兰式的使用：需使用额外的标识符栈。顺序扫描逆波兰表达式的时候，遇到标识符直接入栈。

遇到运算符时：

1. 根据运算符目数，从栈顶取出相应数目的标识符做运算，并把运算结果压栈
2. 运算结束时，标识符栈应该只剩下一个元素，且为运算结果

三元式表示

三元式\((op, A_1, A_2)\)

\(op\)为运算符
\(A_1\)为第一运算对象
\(A_2\)为第二运算对象

例如\(a:=b*c+b*d\)表示为：
\((1)\quad(*,b,c)\)
\((2)\quad(*,b,d)\)
\((3)\quad(+,(1),(2))\quad\) 这里用(1)和(2)来表示中间计算结果的显式引用
\((4)\quad(:=,(3),a)\quad\) 这里相当于\(a:=(3)\)

而单目运算的\(-b\)可以表示成\((-,b,/)\)

树形表示

树形表示和三元式表示非常相似，如\(a:=b*c+b*d\)表示为：

注意赋值表达式中被赋值对象在树的左孩子节点位置

单目运算\(-T_1\)直接表示成：

四元式(三地址码)表示

四元式\((op, A_1, A_2,R)\)

\(op\)为运算符
\(A_1\)为第一运算对象
\(A_2\)为第二运算对象
\(R\)为运算结果

例如\(a:=b*c+b*d\)的四元式表示：
\((1)\quad(*,b,c,t_1)\)
\((2)\quad(*,b,d,t_2)\)
\((3)\quad(+,t_1,t_2,t_3)\)
\((4)\quad(:=,t_3,-,a)\)

和三元式的差别在于，四元式对中间结果的引用必须通过给定的名字(临时变量)

它的三地址码写法为：
\(t_1:=b*c\)
\(t_2:=b*d\)
\(t_3:=t_1*t_2\)
\(a:=t_3\)

翻译

布尔表达式的翻译

布尔表达式在程序设计语言中有两个作用：

1. 计算逻辑值
2. 用于改变控制流语句中的条件表达式

控制流语句包含循环、分支两大类。

通常我们只考虑如下文法生成的布尔表达式：
\(E\rightarrow E\; and\; E\mid E\; or\; E\mid not\; E\mid id\; rop\; id\mid id\mid true\mid false\)
其中\(rop\)是关系符，如\(<=, <, =, >, >=\)等
布尔运算符的优先顺序为\(not>and>or\)
并且\(and\)和\(not\)服从左结合

布尔表达式的计算有两种方法：

1. 计算各部分的真假值，最后计算出整个表达式的值
   \((1\;and\;0)\;and\;(0\;or\;1)=0\;and\;1=0\)
2. 短路法：\(A\;and\;B\)如果\(A=0\)则直接得到\(0\)；\(A\;or\;B\)如果\(A=1\)则直接得到1。这种方式若\(B\)为一个带返回值的过程调用会引发副作用

布尔表达式翻译成四元式序列，如\(a\; or\; b\; and\; not\; c\)的翻译结果为：
\((1)\quad t_1 :=\;not\;c\)
\((2)\quad t_2 :=b\;and\;t_1\)
\((3)\quad t_3 :=a\;or\;t_2\)

条件语句中布尔表达式的翻译

现在有文法：
\(S\rightarrow if\;E\;then\;S1\mid if\;E\;then\;S1\;else\;S2\mid while\;E\;do\;S1\)

翻译这部分的题目主要是以给定四元式序列，然后填空。

对布尔表达式\(E = a\; rop\; b\)，可以翻译成：
\((1)\quad if\;a\;rop\;b\;goto\; E.true\)
\((2)\quad goto\;E.false\)

但此时\(E.true\)和\(E.false\)的值仍不能被确定。例如：
\(S\rightarrow if\;E\;then\;S1\;else\;S2\)

\(E.true\)的值为\(S1\)的第一条四元式的地址
\(E.false\)的值为\(S2\)的第一条四元式的地址

\(if\;af\;then\;S1\;else\;S2\)的四元式序列：

\((1)\quad if\;a
\((2)\quad goto\; \underline{(3)}\)
\((3)\quad if\;c
\((4)\quad goto\; \underline{E.false}\)
\((5)\quad if\;e>f\;goto\; \underline{E.true}\)
\((6)\quad goto\;\underline{E.false}\)
\((7)\quad S1\;begin...\)
\(...\)
\((p-1)\quad ...S1\;end\)
\((p)\quad goto \;\underline{q}\)
\((p+1)\quad S2\;begin...\)
\(...\)
\((q-1)\quad ...S2\;end\)
\((q)\quad ...\)

在产生出S1和S2的状态块后，才能进行地址回填。上面的\(E.true\)应填\((7)\)，而\(E.false\)应填\((p+1)\)。

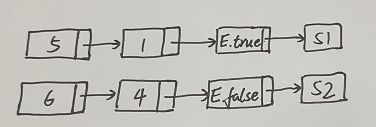
为了解决地址回填的问题，需要采用拉链法，把需要回填\(E.true\)的所有四元式构造并维护一条真链的链表，把需要回填\(E.false\)的所有四元式构造一条假链的链表

对于上面的例子，真链和假链如下图：

其中(5)为真链的链首，(6)为假链的链首。一旦确定S1和S2的地址，就可以沿着链作地址回填

但还有3种情况会使得四元式序列变得十分复杂，这里不讨论：

1. 连续的\(or\)或连续的\(and\)
2. 连续的\(if-else\;if-else\;if...\)
3. 嵌套条件语句

循环语句中布尔表达式翻译

现需要翻译语句：\(while\;a

\(100:\quad if\;a
\(101:\quad goto\; \underline{E.false}\)
\(102:\quad if\;c
\(103:\quad goto\; \underline{106}\)
\(104:\quad t1:=Y+Z\)
\(105:\quad X:=t1\)
\(106:\quad goto\;\underline{100}\)
\(107: \quad...\)

分析到状态块的开始就可以确认\(E.true=102\)，而分析完状态块的结束之后就可以确认\(E.false=107\)

for循环语句翻译

现需要翻译语句：\(for\;I\;:=\;1\;step\;1\;until\;Y\;do\;X:=X+1\)
等价于C语言的：\(for(I=1;I<=Y;++I) X=X+1;\)

\(100:\quad I:=1\)
\(101:\quad goto\;\underline{103}\)
\(102:\quad I:=I+1\)
\(103:\quad if\;I<=Y\;goto\; \underline{105}\)
\(104:\quad goto\; \underline{108}\)
\(105:\quad T:=X+1\)
\(106:\quad X:=T\)
\(107:\quad goto\; \underline{102}\)
\(108: \quad...\)

数组的翻译

对于一个静态的n维数组，要访问其中一个元素，可以使用下标法：
\[A[i_1,i_2,...,i_n]\]

由于内存是一维连续空间，对于行主数组，比如一个\(2\times3\)的二维数组，在内存中的布局为：
\[A[1,1]\;A[1,2]\;A[1,3]\;A[2,1]\;A[2,2]\;A[2,3]\]

现知道数组\(A\)的地址为\(a\)，那\(A[i,j]\)的地址为：
\[a+(i-1)\times 3+(j-1)\]

设\(B\)为n维数组\(B[l_1:u_1,l_2:u_2,...,l_n:u_n]\)

显然\(d_i=u_i-l_i+1\)。令\(b\)是数组首元素地址，那么行主数组下\(B[i_1,i_2,...,i_n]\)的地址\(D\)为：
\[D=b+(i_1-l_1)d_2d_3...d_n+(i_2-l_2)d_3...d_n+(i_{n-1}-l_{n-1})d_n+(i_n-l_n)\]

对式子展开可以提取出式子中的固定部分和变化部分：
\(D=constPart+varPart\)
\(constPart=b-C\)
\(C=l_1d_2d_3...d_n+l_2d_3...d_n+...+l_{n-1}d_{n-1}+l_nd_n\)
\(varPart=i_1d_2d_3...d_n+i_2d_3...d_n+...+i_{n-1}d_{n-1}+i_nd_n\)

访问数组元素\(A[i_1,i_2,...,i_n]\)需要产生两组计算数组的四元式：

1. 一组计算\(varPart\)，存放结果到临时单元\(T\)中
2. 一组计算\(constPart\)，存放结果到另一个临时单元\(T1\)中

用\(T1[T]\)表示数组元素的地址

变址取数的四元式：\((=[],T1[T],-,X)\),相当于\(X:=T1[T]\)
变址存数的四元式：\(([]=,X1,-,T1[T])\),相当于\(T1[T]:=X\)

现在有一个10*20的数组A，即\(d1=10, d2=20\)。则\(X:=A[I,J]\)的四元式序列为：
\((*,I,20,T1)\)
\((+,T1,J,T1)\)
\((-,A,21,T2)\)
\((=[], T2[T1], -, T3)\)
\((:=,T3,-,X)\)

对应：
\(varPart=20*I+J\)
\(constPart=A-(1*20+1)=A-21\)

这一章可能的考点

1. 中间代码的逆波兰表示、树形表示、三元式表示、四元式表示
2. 翻译相关，可能会给出代码进行填空

转载于:https://www.cnblogs.com/X-Jun/p/11040249.html