图解B树
引言
今天去面试
面试官:mysql数据库索引这么快,知道是通过什么实现的吗?
我(一脸懵逼):不知道
面试官淡淡的说:你心里有没有点B数概念?
我:(擦,不就是不知道吗,用得着骂人吗)
当场站起来走了,回去搜了一下,才知道面试官问我知不知道B-树。
今天我们要介绍的就是B树,看完这篇文章之后,我相信你心里一定有B树了。
B树也称B-树,它是一颗平衡的多路搜索树。我们描述一颗B树时需要指定它的阶数,阶数表示一个节点最多有多少个孩子节点,一般用字母m表示阶数。当m取2时,就是我们常见的二叉搜索树。
有时也称M路B树,即有M个分支的B树
多级存储系统中使用B-树,可针对外部查找,大大减少I/O次数。
![]()
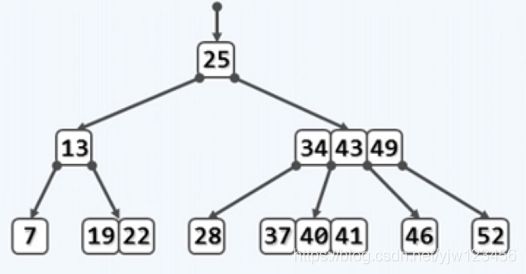
上图就是一颗典型的B树。
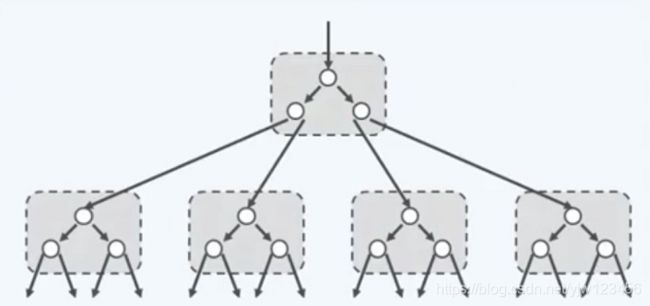
B树的本质是二叉搜索树,如果把B树中的节点称为超级节点的话,那么每个超级节点可以看成是若干个二叉节点经过适当的合并得到的。比如上图,每两代二叉节点合并成一个超级节点,每个超级节点中有3个关键码,有4条分支。
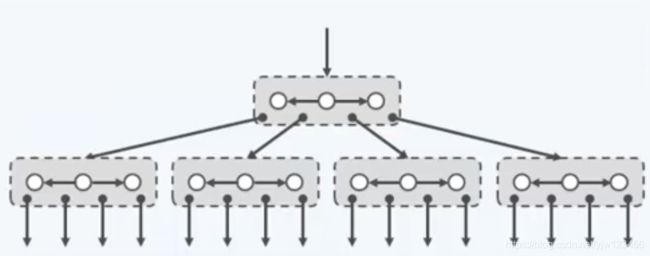
合并后的结果如图所示,这就是一颗4路B树,也可称为(2,4)树
特性
一颗m阶的B树特性如下:
- 内部各节点有:
- 不超过m-1个关键码: K 1 < K 2 < . . . < K n K_1 < K_2 < ... < K_n K1<K2<...<Kn, n个
- 不超过m个分支: A 0 , A 1 , A 2 , . . . , A n A_0,A_1,A_2,...,A_n A0,A1,A2,...,An, n+1个
- 内部节点的分支数n+1有:
- 树根: n + 1 ≥ 2 n+1\geq2 n+1≥2(注:树根也有可能没有任何分支)
- 其他节点: n + 1 ≥ ⌈ m / 2 ⌉ n + 1\geq ⌈m/2⌉ n+1≥⌈m/2⌉ ( ⌈m/2⌉表示向上取整,比如3/2=2,java中可以简单的通过
(3+1)/2来实现)
- 所有叶子节点位于同一层(所有叶子节点深度相等);
完整的表示一颗B树如下:
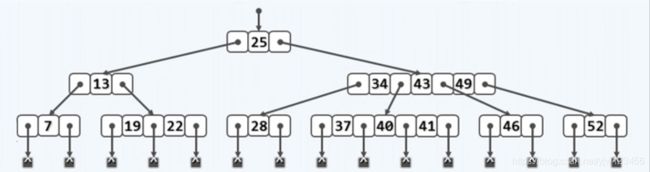
为了简便,我们省略外部节点与引用节点,如下这样描述一颗B树:
实现
结构
我们来观察某一个节点的结构,可以发现,其中有n个关键码以及n+1个分支,m=n+1。
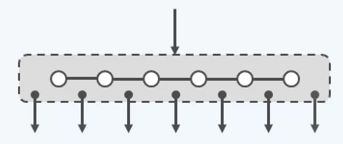
因此,不难理解用两个类似列表的结构就可以表示它们。这么我们用自定义数据结构Vector来表示它们。它的实现在本文末尾。
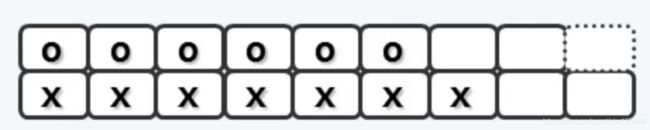
○表示关键码,×表示孩子节点
private class Node implements Comparable<Node> {
Node parent;
//关键字集合
Vector<E> keys = new Vector<>(m);//不超过m-1个关键码,这里没设置成m-1,因为当vector.size() == m时说明上(下)溢了
//分支集合
Vector<Node> children = new Vector<>(m);//不超过m个分支
Node() {
//用来判断是否为叶子节点
children.insert(0, null);
}
E getKey(int index) {
return keys.get(index);
}
void setKey(int index, E e) {
keys.set(index, e);
}
Node getChild(int index) {
return children.get(index);
}
void setChild(int index, Node node) {
children.set(index, node);
}
/**
* 返回当前节点是否为叶子节点
*
* @return
*/
boolean isLeaf() {
return this.children.get(0) == null;
}
/**
* 为该节点在rightRank处插入一个关键码和分支
*
* @param rightRank 要插入的关键码的位置
* @param e 关键码
* @param rightChild 分支
*/
void insertNode(int rightRank, E e, Node rightChild) {
this.keys.insert(rightRank, e);
this.children.insert(rightRank + 1, rightChild);
if (rightChild != null) {
rightChild.parent = this;
}
}
Node(E e, Node lc, Node rc) {
keys.insert(0, e);
children.insert(0, lc);
children.insert(1, rc);
if (lc != null) {
lc.parent = this;
}
if (rc != null) {
rc.parent = this;
}
}
@Override
public int compareTo(Node other) {
//比较当前节点和other的最大值
return this.keys.getLast().compareTo(other.keys.getLast());
}
}
下面我们先来一起探讨下B树中最简单也是最重要的操作——查找是如何进行的
查找
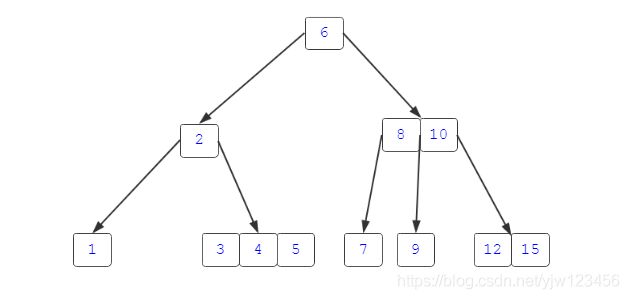
给定一颗B树,我们如何进行查找呢?比如,我们要查找关键码5。
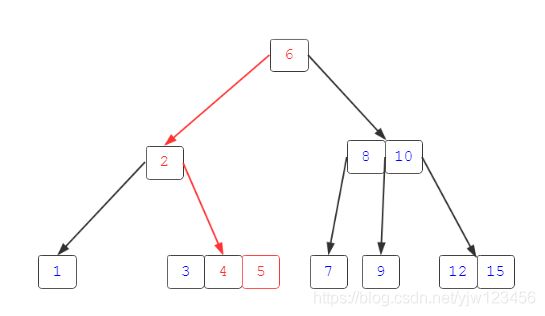
首先,访问根节点6,然后查找小于它的做孩子节点2,它只有一个关键码,但是仍然不是我们要找的值,因为5比2大,继续沿着它的右孩子[3,4,5],此时,有不止一个关键码,我们可以顺序比较,也可以二分比较。假设这里我们二分比较,首先比较关键码4,向右比较关键码5,bingo,就是它。存在,说明找到了。
那么,如果查找一个不存在的关键码,比如11,会怎样呢?
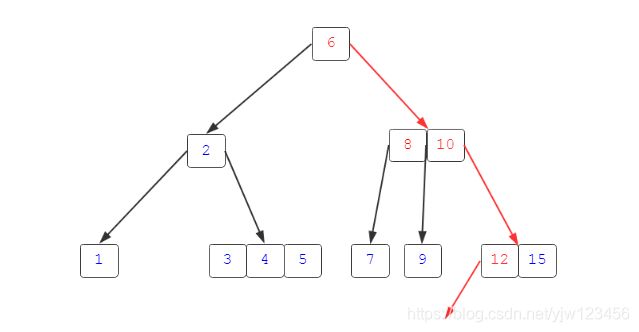
我就不逐步描述了,通过上图也不难理解,注意,最后访问到了关键码12的做孩子,它指向了null,因此说明查找失败。
有时,这并不是查找失败,而是加载外部节点到内存中,继续查找。这里为了简单,我们就不考虑这种情况。
private Node search(E e) {
Node p = root;//通过p遍历整棵树
lastReachedNode = null;//用于记录最后一个访问的节点,可用于插入
while (p != null) {//p不为空就一直进行下去
int rank = p.keys.search(e);//rank表示关键码列表中<=e的元素的最大值的索引
if (rank >= 0 && e.compareTo(p.getKey(rank)) == 0) { //若结果>=0,不一定表示找到了,还可能指向的是小于该关键码的最大值索引
//一定是在p.keys[rank] == e的情况下才能说明找到了
return p;
}
lastReachedNode = p;//缓存最后访问的节点p
//继续查找失败节点的右孩子,因为之前返回的是小于e的节点,因此应该向它的右分支查找
p = p.getChild(rank + 1);
}
return null;
}
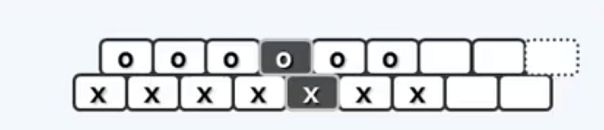
我们将关键码列表和分支列表错位,可以更容易看出每个关键码和其左右分支的关系。
插入
嘿嘿,第二个介绍插入实现是因为它依赖于查找,同时查找是最简单的所以最先介绍。
public boolean insert(E e) {
Node node = search(e);//调用B树的查找算法
if (node != null) {
//已经存在
return false;
}
//在最后访问的节点中得到要插入的位置(不大于目标关键码的最大关键码的位置)
int rank = lastReachedNode.keys.search(e); //该lastReachedNode必为叶节点(它的分支都为空),不然还会继续查找下去
//将其插入该位置之后
lastReachedNode.keys.insert(rank + 1, e);
//同时,多插入一个空右分支
lastReachedNode.children.insert(rank + 2, null);
size++;
//可能发生上溢:分支数超过阶次m,通过拆分(split)来处理上溢
split(lastReachedNode);
return true;
}
如果不考虑上溢的情况,其实插入实现也很简单。只要找到待拆入位置,插入即可。
但是,世界是复杂的。插入时由于多加了一个关键码和一个分支,可能导致节点的分支数超过m(称这种情况为上溢),此时不满足B树的定义了,因此需要处理这种情况。我们通过分裂来处理。
分裂
分裂从字面意思来看,就是将一个节点分裂成两个,那么是如何分的呢?
- 我们将上溢节点中的关键码记为: k 0 , . . . , k m − 1 k_0,...,k_{m-1} k0,...,km−1 (从0开始哦,有m个了)
- 取中位数s = ⌊m/2⌋(表示向下取整,java中的
/就是向下取整),以关键码 K s K_s Ks为界分为: k 0 , . . . , k s − 1 k_0,...,k_{s-1} k0,...,ks−1 , K s K_s Ks , k s + 1 , . . . , k m − 1 k_{s+1},...,k_{m-1} ks+1,...,km−1 - 关键码 k s k_s ks提升至父节点(有的话)
- 以分裂所得的两个节点作为 k s k_s ks的左右孩子(分支)
还是通过图示来理解这个过程吧,假设在一颗6阶B树(节点最多5个关键码,或者说最多有6个分支)中插入关键码37:
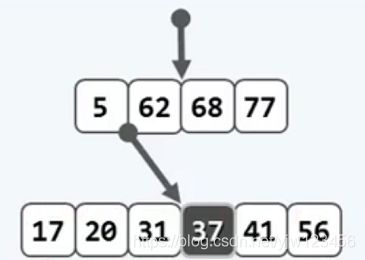
导致发生了上溢,我们在这6个关键码中选取中位数:6/2=3(m/2),指向的关键码为37。
我们将该节点以37为界进行分裂,分裂为两个节点[17,20,31]与[41,56],并将37提升到父节点中,这两个节点作为它的左右孩子。
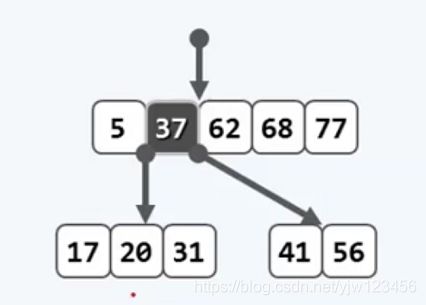
尽管这两个分裂出来的节点关键码数量比分裂前几乎少了一半,但还是会满足B树关于关键码所设的下限。
我们回顾下B树的定义,分支数m = 关键码数n+ 1
m >= ⌈M/2⌉ ,M为B树的阶数
n+1 >= ⌈M/2⌉
得关键码数n >= ⌈M/2⌉ - 1
这里M=6,关键码数的下限为3-1=2,因此可以看出,为啥有分支数 >= ⌈阶数/2⌉ 这个定义
虽然被分裂的节点不会再上溢了,但是因为提升了一个关键码到父节点,父节点也是有可能发生上溢的,此时,重复这个过程即可…直到根节点发生上溢(也就是说,它的父节点为空)
如果根节点也发生了上溢,同样取出中位数关键码,将提升后的关键码成为新的根节点。同时整颗树的高度提升1。根节点只有1个关键码也是符合定义的。回顾树根的分支数下限定义: n + 1 ≥ 2 n+1\geq2 n+1≥2 → n ≥ 1 n\geq1 n≥1,即树根关键码数只要大于等于1即可。同样可以看出这样设计的奥妙所在。同时该新根节点的分支数也满足大于等于2的条件。

如上图左所示,假设[17,20,31,37,41,56]为根节点,发生了上溢,处理后结果如上图右所示。
从如上过程可以看出,最多分裂树高h次,因此,整个插入算法的时间复杂度为 O ( h ) O(h) O(h)
/**
* 分裂,解决上溢
*
* @param node
*/
private void split(Node node) {
//判断是否需要分裂
if (node.children.size() <= m) {
return;
}
int s = m / 2; //取中位数s,以关键字k_s为界划分为: k_0,...,k_(s-1), k_s ,k_(s+1),...,k_(m_1)
Node newNode = new Node();//新节点已有一个空分支
for (int i = 0; i < m - s - 1; i++) {
//将s+1到m-1的元素(包括关键码和分支)逐个移到newNode中 ,共有 m-1-(s+1)+1 = m-s-1个 即endIndex-startIndex+1
newNode.children.insert(i, node.children.remove(s + 1));//移动分支
newNode.keys.insert(i, node.keys.remove(s + 1));//移动关键码
}
//移动node的最后一个分支到newNode中,此时node的关键码数和分支数相同,那是因为中位数关键码还未提升
newNode.setChild(m - s - 1, node.children.remove(s + 1));
if (!newNode.isLeaf()) {
//如果新节点不是叶子节点,新节点有m-s个分支,设置其分支的父节点指向它
for (int i = 0; i < m - s; i++) { //设置父节点
newNode.getChild(i).parent = newNode;
}
}
Node p = node.parent;//获取node当前的父节点p,若p不为空,它的左孩子已经指向node了,不需要修改,只要让其右孩子指向newNode
if (p == null) { //如果分裂的是根节点
p = new Node();
root = p;
p.setChild(0, node);//node作为新父节点的左孩子,后面有newNode作为它的右孩子
node.parent = p;
}
//得到中位数关键码在p节点中的合适位置
//不大于中位数的最大元素的位置 + 1,注意这种处理手法,多次出现
int rank = 1 + p.keys.search(node.getKey(0));
//中位数对应关键码上升,newNode作为它的右孩子
p.insertNode(rank, node.keys.remove(s), newNode);
//上升一层,可能需要继续分裂
split(p);
}
我们构造一颗(2,3)树,并通过图示来分析一下它的插入过程
public static void main(String[] args) {
BTree<Integer> tree = new BTree<>(3);
int[] values = {8, 3, 2, 1, 6, 7, 9, 12, 15};
for (int value : values) {
tree.insert(value);
}
System.out.println(tree.size());
}
我们一步一步来构造这颗阶数为3的2-3树
插入8
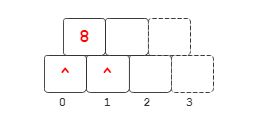
此时这是一颗最简单的B树,^ 代表null, 红 色 \color{red}{红色} 红色代表最近插入的关键码或分支,此时根节点无分支,或者说有两个空分支。
插入3
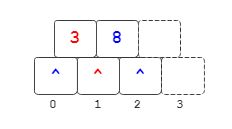
3是插入到关键码8前面,它的又分支也是一样,插入操作会将已存在的元素向右移动,这里 蓝 色 \color{blue}{蓝色} 蓝色表示原来的关键码或分支。
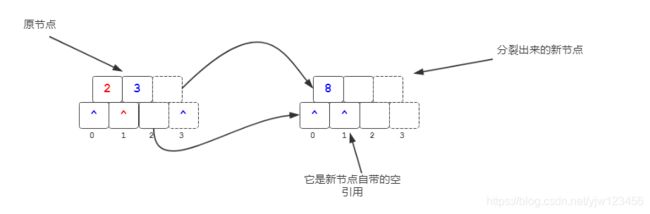
插入2
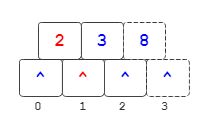
插入完2的节点上所示,注意,此时不是最终状态。每次插入完之后会判断是否上溢,此时有4个分支,超过了阶数3,发生了上溢。我们要对该节点进行分裂操作:
取中位数(3/2=1)对应的关键码3,将该节点分裂为两个节点,3右边的关键码全部移到新节点上去。
同时将关键码对应的左分支移动到新节点上,就是上图左边分支列表索引2处的元素移到到了右边0处。移动完之后,分支索引3处的元素会左移一位,然后将它移动新阶段关键码8的右孩子分支处。
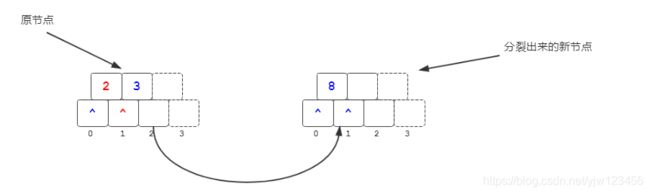
也就是将中位数元素后的所有关键码和分支(分支会比关键码数量多1)全部移动到新分支上。
细心的同学会发现,此时上图左边的节点有两个关键码和两个分支,似乎多了一个分支。别急,还有一个步骤,将中位数上的关键码(也就是3)向上提升到父节点(可能没有,这里就没有)
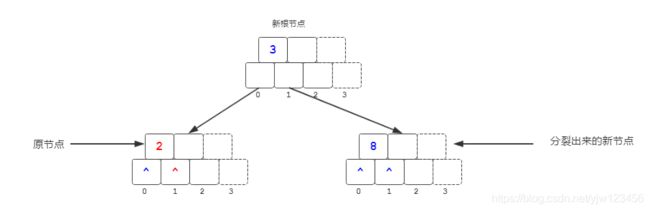
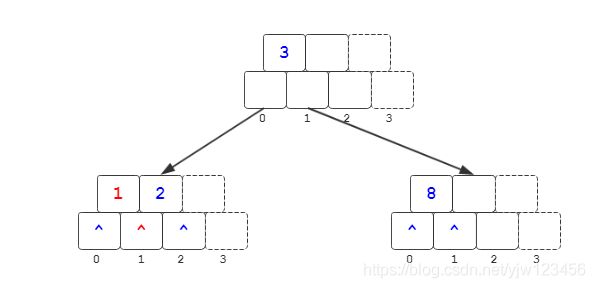
因为此时分裂的就是根节点,因此直接构造出一个新节点作为根节点,将它的左右孩子分别指向原节点和分裂出来的新节点。同时更新孩子的父节点引用。(这里没有画出来父节点引用) 至此,才是一个完整的插入并分裂结果。
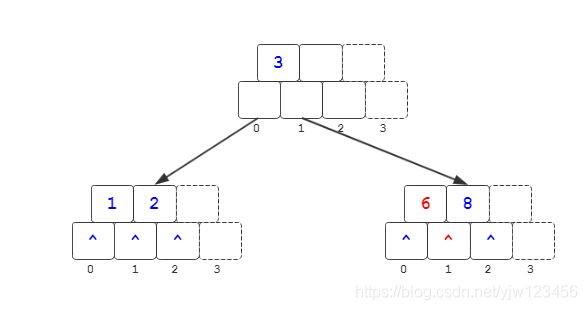
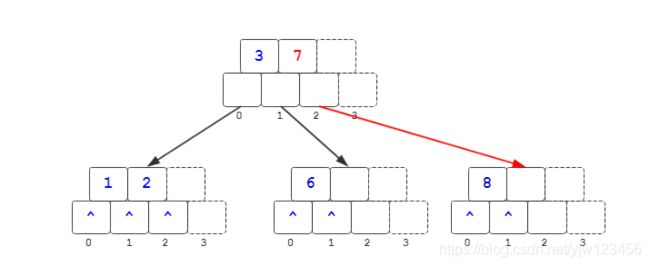
插入6
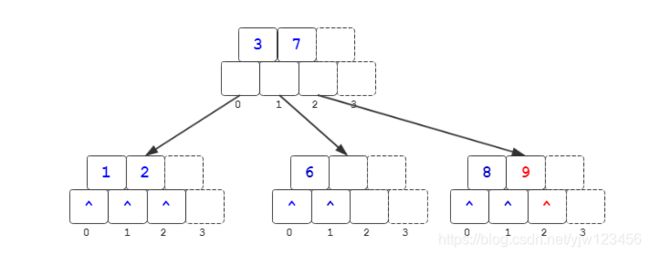
插入7
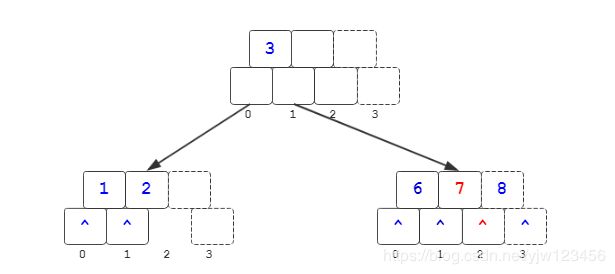
我们进行查询操作后,得到最后访问的关键码为6,因此在其后插入关键码7。此时也发生了上溢,过程和我们前面分析的一样,就不展开分析了。
最终结果为:
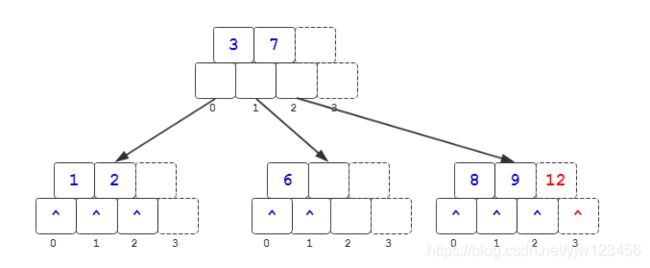
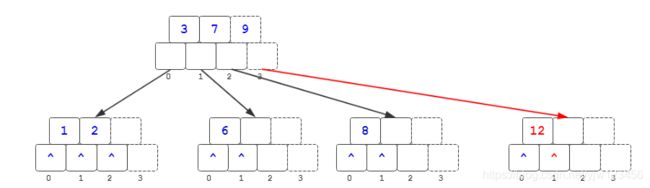
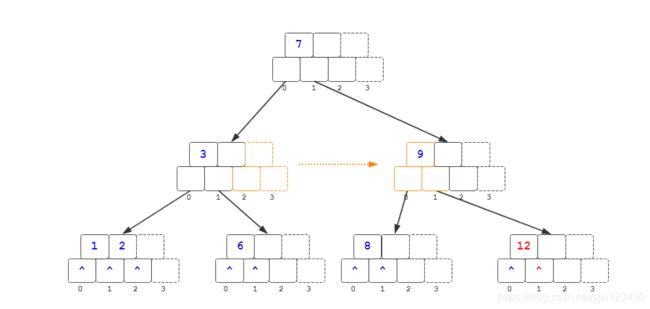
首先是插入到[8,9]节点上,插入了关键字12后,导致上溢,将[8,9,12]分裂后:
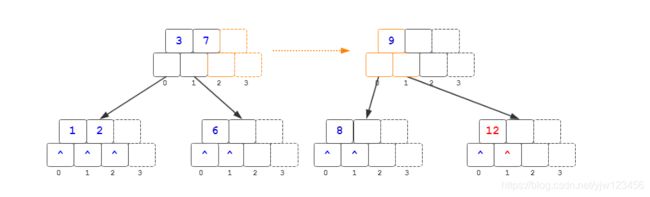
将父节点的9关键码分裂出来后的快照如上,此时中位关键码7还未提升,可以从图中看出,相当于是将关键码9的左孩子以及最后一个节点(这里也是9,但要知道可能不止移动一个关键码)的右孩子移动到分裂出的节点。
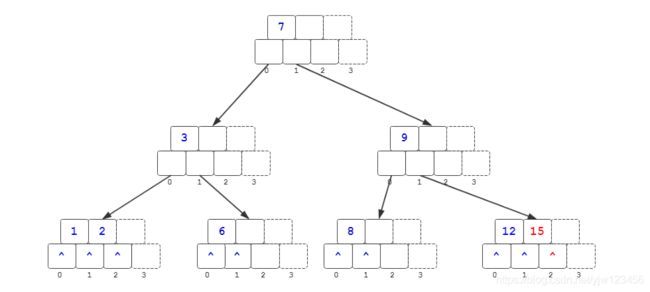
插入15
删除
几乎所有的树中,删除算法是最复杂的。B树叶不例外,但是还是可以弄明白的。
public boolean remove(E e) {
//首先还是先查询是否存在
Node node = search(e);
if (node == null) {
return false;
}
int rank = node.keys.search(e);//得到e在节点中的位置
if (!node.isLeaf()) {//如果非叶子,则找到后继节点
Node p = node.children.get(rank + 1);//右子树中一直向左
//找到node的后继节点
while (!p.isLeaf()) {
p = p.children.get(0);
}
//将node与后继节点交换位置
node.keys.set(rank, p.getKey(0));
node = p;
rank = 0;
}
//此时node位于最底层,其中第rank个关键码就是待删除者
//除了要删除关键码,还要删除该关键码的右分支
node.keys.remove(rank);
node.children.remove(rank + 1);
size--;
//解决下溢问题
solveUnderflow(node);
return true;
}
删除算法的主线和BST差不多,但是由于删除节点后可能会导致某个节点的分支数少于限定值,这种情况称为下溢,下面重点来分析下该问题如何解决。
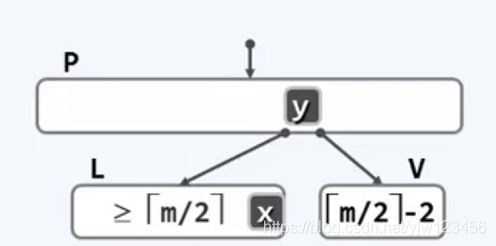
若节点V下溢时,它必然比最小关键码限定少一个关键码,即:⌈m/2⌉ - 2个关键码和⌈m/2⌉ - 1个分支。
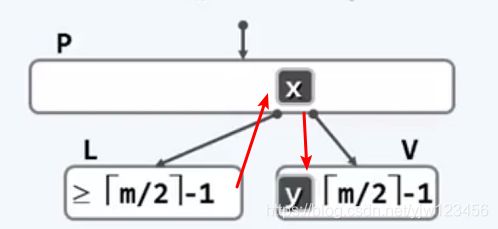
- 若V节点的兄弟节点(左或右)的关键码足够多(>= ⌈m/2⌉ )关键码,假设它的左兄弟满足这种情况,此时可以从左兄弟(右兄弟同理)借一个(当然是不会还的哈哈)关键码到节点V。这里需要注意到,不能直接把做兄弟的最后一个孩子移到V中,因为这样不能符合中序遍历上的顺序性(父节点关键码大于左分支关键码小于右分支关键码),因此实际上的做法是将x移到父节点,同时将父节点关键码y移动V节点。、
- 若V的左兄弟L和右兄弟R或不存在,或所包含的关键码数不足 ⌈m/2⌉ 个(那就是刚好 ⌈m/2⌉ -1个),但是左右兄弟必有一个存在(因为所有的叶子节点都在同一层上,极端情况是最左边的节点只有右兄弟,而最右边的节点只有左兄弟),这里假设左兄弟L存在。此时,假设将L和V以及父节点关键y合并成一个新节点,该新节点的关键码数为: ⌈m/2⌉ - 1 + 1 + ⌈m/2⌉ - 2 (L的关键码数 +父节点一个关键码 + V节点关键数 ) = m - 2 ,注意该值小于关键码数的上限(m-1)。
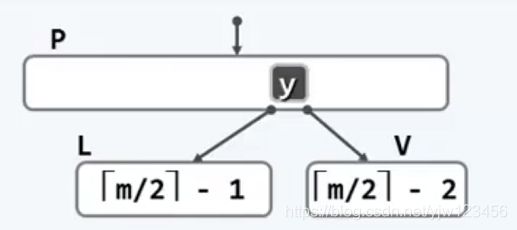
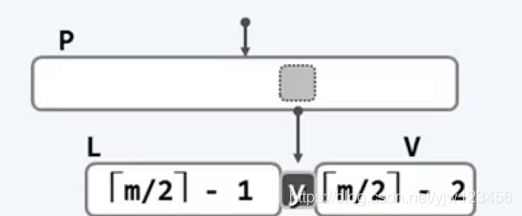
注意,由于从父节点拉了一个关键码下来,可能导致父节点也发生下溢,重复整个处理下溢过程即可。
整个修复下溢过程迭代数不超过 O ( h ) O(h) O(h)。
/**
* 解决下溢问题:删除后关键码数量不满足B树定义:不小于ceil(m/2)
*
* @param node
*/
private void solveUnderflow(Node node) {
//并未下溢
if (node.children.size() >= ceilHalfM) {
return;
}
Node p = node.parent;
if (p == null) {
//已经到了根节点,没有分支的下限
if (node.keys.size() == 0 && node.getChild(0) != null) {
//树根已不含有关键码,却有唯一的非空孩子,将它作为新根,这是整颗树高度下降的唯一场景
root = node.getChild(0);
root.parent = null;
node.setChild(0, null);//node对应的引用可被回收了
}
return;
}
//还未达到根节点
//确定node是p的第rank个孩子,此时p可能不含关键码,不能通过关键码查找
int rank = 0;
while (node.compareTo(p.getChild(rank)) != 0) {
rank++;
}
//向左兄弟借关键码
if (rank > 0) {
//若node不是p的第一个孩子,必存在左兄弟
Node ls = p.getChild(rank - 1);//left sibling : ls
if (ls.children.size() > ceilHalfM) {//若左兄弟的关键码足够
//rank - 1关键码处的右孩子是rank
node.keys.insert(0, p.getKey(rank - 1));//这里借的是对应的父节点的关键码
p.setKey(rank - 1, ls.keys.remove(rank - 1));//将左兄弟最大的关键码提升到父节点位置
//将左兄弟最右侧的孩子给node
node.children.insert(0, ls.children.remove(ls.children.size() - 1));
if (!node.isLeaf()) {
//如果该孩子不是空还需要修改parent引用
node.children.get(0).parent = node;
}
return;
}
//若左兄弟关键码不够
}
//代码到了这里说明 左兄弟为空或 左兄弟关键码数不够
//若有右兄弟,向右兄弟借关键码,和向左兄弟借关键码是一个镜像操作
if (p.children.size() - 1 > rank) {
Node rs = p.getChild(rank + 1);
//若右兄弟关键码数足够
if (rs.children.size() > ceilHalfM) {
//p借出一个关键码给node,作为最大者
node.keys.insert(node.keys.size(), p.getKey(rank));
p.setKey(rank, rs.keys.remove(0));//右兄弟最小关键码提升
node.children.insert(node.children.size(), rs.children.remove(0));
if (node.getChild(node.children.size() - 1) != null) {
node.getChild(node.children.size() - 1).parent = node;
}
return;
}
}
//代码执行到此,说明左,右兄弟要么为空(左右兄弟至少有一个不为空),要么关键码数不够
if (rank > 0) { //说明左兄弟不为空,合并到左兄弟
Node ls = p.getChild(rank - 1);
//首先将父节点rank-1处关键码下移到左兄弟
ls.keys.insert(ls.keys.size(), p.keys.remove(rank - 1));
p.children.remove(rank);//下移后指向node的分支删除掉
//node的最左侧孩子过继给ls做最右侧孩子
ls.children.insert(ls.children.size(), node.children.remove(0));
if (ls.getChild(ls.children.size() - 1) != null) {
ls.getChild(ls.children.size() - 1).parent = ls;
}
//将node剩余的关键码和孩子移动到ls
while (!node.keys.isEmpty()) {
ls.keys.insert(ls.keys.size(), node.keys.remove(0));
ls.children.insert(ls.children.size(), node.children.remove(0));
if (ls.getChild(ls.children.size() - 1) != null) {
ls.getChild(ls.children.size() - 1).parent = ls;
}
}
} else {
//与右兄弟合并
Node rs = p.getChild(rank + 1);
rs.keys.insert(0, p.keys.remove(rank));
p.children.remove(rank);
rs.children.insert(0, node.children.remove(node.children.size() - 1));
if (rs.getChild(0) != null) {
rs.getChild(0).parent = rs;
}
while (!node.keys.isEmpty()) {
rs.keys.insert(0, node.keys.remove(node.keys.size() - 1));
if (rs.getChild(0) != null) {
rs.getChild(0).parent = rs;
}
}
}
//可能父节点p也下溢了
solveUnderflow(p);
}
完整代码
BTree:
package com.algorithms.tree;
import com.algorithms.list.Vector;
/**
* m路B树,路就是分支的意思,说明有m个分支,相应的就有m-1个关键码
* 不超过m-1个关键码(key),关键码按递增次序排列,不超过m个分支(孩子)
* 树根的分支数 >=2(或者仅存在合法的根节点,无分支)
* 其他节点的分支数至少为ceil(m/2)
* 每个节点最多含有m个分支
*
* @author yjw
* @date 2019/7/1/001
*/
public class BTree<E extends Comparable<? super E>> {
private static final int DEFAULT_M = 3;//(2,3)树
private int size;
private Node root;
private final int m; //阶数
private Node lastReachedNode;
private final int ceilHalfM;//ceil(m/2)
public BTree(int m) {
//必须是大于2
if (m <= 2) {
throw new IllegalArgumentException("m mast be greater than 2");
}
this.m = m;
size = 0;
root = new Node();
this.ceilHalfM = (m + 1) / 2;//(m+1)/2 就是ceil(m/2) ceil是天花板,取上限的意思
}
public BTree() {
this(DEFAULT_M);
}
public int size() {
return size;
}
private Node search(E e) {
Node p = root;
lastReachedNode = null;
while (p != null) {
int rank = p.keys.search(e);
if (rank >= 0 && e.compareTo(p.keys.get(rank)) == 0) {
//找到了
return p;
}
lastReachedNode = p;
p = p.children.get(rank + 1);
}
return null;
}
public boolean insert(E e) {
Node node = search(e);
if (node != null) {
//已经存在
return false;
}
//在lastReachedNode中确定插入位置,lastReachedNode必然是叶子节点
int rank = lastReachedNode.keys.search(e);
lastReachedNode.insertNode(rank + 1, e, null);
size++;
split(lastReachedNode);
return true;
}
/**
* 分裂,解决上溢
*
* @param node
*/
private void split(Node node) {
//判断是否需要分裂
if (node.children.size() <= m) {
return;
}
int s = m / 2; //取中位数s,以关键字k_s为界划分为: k_0,...,k_(s-1), k_s ,k_(s+1),...,k_(m_1)
Node newNode = new Node();//新节点已有一个空分支
for (int i = 0; i < m - s - 1; i++) {
//将s+1到m-1的元素(包括关键码和分支)逐个移到newNode中 ,共有 m-1-(s+1)+1 = m-s-1个 即endIndex-startIndex+1
newNode.children.insert(i, node.children.remove(s + 1));//移动分支
newNode.keys.insert(i, node.keys.remove(s + 1));//移动关键码
}
//移动node的最后一个分支到newNode中,此时node的关键码数和分支数相同,那是因为中位数关键码还未提升
newNode.setChild(m - s - 1, node.children.remove(s + 1));
if (!newNode.isLeaf()) {
//如果新节点不是叶子节点,新节点有m-s个分支,设置其分支的父节点指向它
for (int i = 0; i < m - s; i++) { //设置父节点
newNode.getChild(i).parent = newNode;
}
}
Node p = node.parent;//获取node当前的父节点p,若p不为空,它的左孩子已经指向node了,不需要修改,只要让其右孩子指向newNode
if (p == null) { //如果分裂的是根节点
p = new Node();
root = p;
p.setChild(0, node);//node作为新父节点的左孩子,后面有newNode作为它的右孩子
node.parent = p;
}
//得到中位数关键码在p节点中的合适位置
//不大于中位数的最大元素的位置 + 1,注意这种处理手法,多次出现
int rank = 1 + p.keys.search(node.getKey(0));
//中位数对应关键码上升,newNode作为它的右孩子
p.insertNode(rank, node.keys.remove(s), newNode);
//上升一层,可能需要继续分裂
split(p);
}
public boolean remove(E e) {
//首先还是先查询是否存在
Node node = search(e);
if (node == null) {
return false;
}
int rank = node.keys.search(e);//得到e在节点中的位置
if (!node.isLeaf()) {//如果非叶子,则找到后继节点
Node p = node.children.get(rank + 1);//右子树中一直向左
//找到node的后继节点
while (!p.isLeaf()) {
p = p.children.get(0);
}
//将node与后继节点交换位置
node.keys.set(rank, p.getKey(0));
node = p;
rank = 0;
}
//此时node位于最底层,其中第rank个关键码就是待删除者
//除了要删除关键码,还要删除该关键码的右分支
node.keys.remove(rank);
node.children.remove(rank + 1);
size--;
//解决下溢问题
solveUnderflow(node);
return true;
}
/**
* 解决下溢问题:删除后关键码数量不满足B树定义:不小于ceil(m/2)
*
* @param node
*/
private void solveUnderflow(Node node) {
//并未下溢
if (node.children.size() >= ceilHalfM) {
return;
}
Node p = node.parent;
if (p == null) {
//已经到了根节点,没有分支的下限
if (node.keys.size() == 0 && node.getChild(0) != null) {
//树根已不含有关键码,却有唯一的非空孩子,将它作为新根,这是整颗树高度下降的唯一场景
root = node.getChild(0);
root.parent = null;
node.setChild(0, null);//node对应的引用可被回收了
}
return;
}
//还未达到根节点
//确定node是p的第rank个孩子,此时p可能不含关键码,不能通过关键码查找
int rank = 0;
while (node.compareTo(p.getChild(rank)) != 0) {
rank++;
}
//向左兄弟借关键码
if (rank > 0) {
//若node不是p的第一个孩子,必存在左兄弟
Node ls = p.getChild(rank - 1);//left sibling : ls
if (ls.children.size() > ceilHalfM) {//若左兄弟的关键码足够
//rank - 1关键码处的右孩子是rank
node.keys.insert(0, p.getKey(rank - 1));//这里借的是对应的父节点的关键码
p.setKey(rank - 1, ls.keys.remove(rank - 1));//将左兄弟最大的关键码提升到父节点位置
//将左兄弟最右侧的孩子给node
node.children.insert(0, ls.children.remove(ls.children.size() - 1));
if (!node.isLeaf()) {
//如果该孩子不是空还需要修改parent引用
node.children.get(0).parent = node;
}
return;
}
//若左兄弟关键码不够
}
//代码到了这里说明 左兄弟为空或 左兄弟关键码数不够
//若有右兄弟,向右兄弟借关键码,和向左兄弟借关键码是一个镜像操作
if (p.children.size() - 1 > rank) {
Node rs = p.getChild(rank + 1);
//若右兄弟关键码数足够
if (rs.children.size() > ceilHalfM) {
//p借出一个关键码给node,作为最大者
node.keys.insert(node.keys.size(), p.getKey(rank));
p.setKey(rank, rs.keys.remove(0));//右兄弟最小关键码提升
node.children.insert(node.children.size(), rs.children.remove(0));
if (node.getChild(node.children.size() - 1) != null) {
node.getChild(node.children.size() - 1).parent = node;
}
return;
}
}
//代码执行到此,说明左,右兄弟要么为空(左右兄弟至少有一个不为空),要么关键码数不够
if (rank > 0) { //说明左兄弟不为空,合并到左兄弟
Node ls = p.getChild(rank - 1);
//首先将父节点rank-1处关键码下移到左兄弟
ls.keys.insert(ls.keys.size(), p.keys.remove(rank - 1));
p.children.remove(rank);//下移后指向node的分支删除掉
//node的最左侧孩子过继给ls做最右侧孩子
ls.children.insert(ls.children.size(), node.children.remove(0));
if (ls.getChild(ls.children.size() - 1) != null) {
ls.getChild(ls.children.size() - 1).parent = ls;
}
//将node剩余的关键码和孩子移动到ls
while (!node.keys.isEmpty()) {
ls.keys.insert(ls.keys.size(), node.keys.remove(0));
ls.children.insert(ls.children.size(), node.children.remove(0));
if (ls.getChild(ls.children.size() - 1) != null) {
ls.getChild(ls.children.size() - 1).parent = ls;
}
}
} else {
//与右兄弟合并
Node rs = p.getChild(rank + 1);
rs.keys.insert(0, p.keys.remove(rank));
p.children.remove(rank);
rs.children.insert(0, node.children.remove(node.children.size() - 1));
if (rs.getChild(0) != null) {
rs.getChild(0).parent = rs;
}
while (!node.keys.isEmpty()) {
rs.keys.insert(0, node.keys.remove(node.keys.size() - 1));
if (rs.getChild(0) != null) {
rs.getChild(0).parent = rs;
}
}
}
//可能父节点p也下溢了
solveUnderflow(p);
}
/**
* 此处Node定义为内部类,非静态类(有static关键字),因此可以访问其关联类的属性(m)和类型参数E
*
* @param
*/
private class Node implements Comparable<Node> {
Node parent;
//关键字集合
Vector<E> keys = new Vector<>(m);//不超过m-1个关键码,这里没设置成m-1,因为当vector.size() == m时说明上(下)溢了
//分支集合
Vector<Node> children = new Vector<>(m);//不超过m个分支
Node() {
//用来判断是否为叶子节点
children.insert(0, null);
}
E getKey(int index) {
return keys.get(index);
}
void setKey(int index, E e) {
keys.set(index, e);
}
Node getChild(int index) {
return children.get(index);
}
void setChild(int index, Node node) {
children.set(index, node);
}
/**
* 返回当前节点是否为叶子节点
*
* @return
*/
boolean isLeaf() {
return this.children.get(0) == null;
}
/**
* 为该节点在rightRank处插入一个关键码和分支
*
* @param rightRank 要插入的关键码的位置
* @param e 关键码
* @param rightChild 分支
*/
void insertNode(int rightRank, E e, Node rightChild) {
this.keys.insert(rightRank, e);
this.children.insert(rightRank + 1, rightChild);
if (rightChild != null) {
rightChild.parent = this;
}
}
Node(E e, Node lc, Node rc) {
keys.insert(0, e);
children.insert(0, lc);
children.insert(1, rc);
if (lc != null) {
lc.parent = this;
}
if (rc != null) {
rc.parent = this;
}
}
@Override
public int compareTo(Node other) {
//比较当前节点和other的最大值
return this.keys.getLast().compareTo(other.keys.getLast());
}
}
public static void main(String[] args) {
BTree<Integer> tree = new BTree<>(3);
int[] values = {8, 3, 2, 1, 6, 7, 9, 12, 15};
for (int value : values) {
tree.insert(value);
}
System.out.println(tree.size());
tree.remove(1);
System.out.println(tree.size);
}
}
Vector:
package com.algorithms.list;
import java.util.Arrays;
import java.util.NoSuchElementException;
/**
* 向量
*
* @author yjw
* @date 2019/6/27/027
*/
public class Vector<E extends Comparable<? super E>> {
private static final int DEFAULT_CAPACITY = 10;
private static final Comparable[] EMPTY_ELEMENT_DATA = {};
/**
* 向量的容量
*/
private int capacity;
/**
* 向量中元素个数
*/
private int size;
//这里设置成泛型数组 参考https://blog.csdn.net/yjw123456/article/details/93666945
private E[] items;
@SuppressWarnings("unchecked")
public Vector(int capacity) {
if (capacity < 0) {
throw new IllegalArgumentException("Negative capacity");
} else if (capacity == 0) {
items = (E[]) EMPTY_ELEMENT_DATA;
} else {
items = (E[]) new Comparable[capacity];
}
this.capacity = capacity;
this.size = 0;
}
public Vector() {
this(DEFAULT_CAPACITY);
}
/**
* 得到索引index处的值
*
* @param index
* @return
*/
public E get(int index) {
checkIndex(index);
return items[index];
}
/**
* 替换索引index处的值
*
* @param index
* @param e
* @return 旧值
*/
public E set(int index, E e) {
checkIndex(index);
E old = items[index];
items[index] = e;
return old;
}
public int size() {
return size;
}
public E getLast() {
if (isEmpty()) {
throw new NoSuchElementException();
}
return items[size - 1];
}
/**
* 在索引index处插入元素e
*
* @param index
* @param e
* @return
*/
public void insert(int index, E e) {
checkIndex(index);
ensureCapacity(size + 1);
//将index及index之后的元素后移
for (int i = size - 1; i >= index; i--) {
items[i + 1] = items[i];
}
items[index] = e;
size++;
}
public boolean isEmpty() {
return size == 0;
}
/**
* @param e
* @return index: 不大于(<=)该项e的元素的最大值的索引
*/
public int search(E e) {
if (isEmpty()) {
return -1;
}
//基于items是有序的
return search(e, 0, size);
}
/**
* [low,high)
*
* @param e
* @param low
* @param high
* @return
*/
private int search(E e, int low, int high) {
while (low < high) {
int mid = low + (high - low) / 2;
int cmp = e.compareTo(items[mid]);
if (cmp < 0) {
high = mid;
} else if (cmp > 0) {
low = mid + 1;
} else {
return mid;
}
}
return low - 1;
}
public void add(E e) {
ensureCapacity(size + 1);
items[size++] = e;
}
public E remove(int index) {
checkIndex(index);
E removed = items[index];
for (int i = index; i < size - 1; i++) {
items[i] = items[i + 1];
}
size--;
return removed;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder("[");
for (int i = 0; i < size; i++) {
sb.append(items[i]);
if (i >= size - 1) {
return sb.append("]").toString();
}
sb.append(", ");
}
return sb.append("]").toString();
}
/**
* 对向量中元素进行排序
*/
public void sort() {
//通过归并排序的方式
mergeSort(items, 0, size);
}
private void checkIndex(int index) {
if (index < 0) {
throw new IndexOutOfBoundsException("index :" + index);
}
}
private void ensureCapacity(int minCapacity) {
if (items == EMPTY_ELEMENT_DATA) {
minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity);
}
if (minCapacity - capacity > 0) {
capacity = minCapacity * 2;
items = Arrays.copyOf(items, capacity);
}
}
private void mergeSort(E[] array, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
/**
* mid属于左边的数组,mid+1属于右边的数组
*/
mergeSort(array, left, mid);//对前半段排序
mergeSort(array, mid + 1, right);//对右半段排序
//优化:如果array[mid]小于array[mid+1],则不需要进行归并了
if (array[mid].compareTo(array[mid + 1]) < 0) {
return;
}
// 归并
// 注意,传入的是mid+1
merge(array, left, mid + 1, right);
}
}
/**
* @param array
* @param left 指向左边数组,左边数组开始位置
* @param right 指向右边数组,右边数组开始位置
* @param rightEnd 右边数组最后一个元素位置
*/
private void merge(E[] array, int left, int right, int rightEnd) {
@SuppressWarnings("unchecked")
E[] aux = (E[]) new Comparable[array.length];//辅助数组
int leftEnd = right - 1;//左边数组最后位置
int auxIndex = left;//辅助数组开始位置
int num = rightEnd - left + 1;//元素总数
while (left <= leftEnd && right <= rightEnd) {
if (array[left].compareTo(array[right]) < 0) {
aux[auxIndex++] = array[left++];
} else {
aux[auxIndex++] = array[right++];
}
}
/**
* 拷贝剩下的元素
* 以下两个while循环,只有一个会执行
*/
while (left <= leftEnd) {
aux[auxIndex++] = array[left++];
}
while (right <= rightEnd) {
aux[auxIndex++] = array[right++];
}
//将辅助数组拷贝回原数组
for (int i = 0; i < num; i++, rightEnd--) {
array[rightEnd] = aux[rightEnd];
}
}
public static void main(String[] args) {
int[] values = {1, 2, 3, 5, 7, 9, 10, 12, 13, 15};
Vector<Integer> vector = new Vector<>();
for (int value : values) {
vector.add(value);
}
vector.insert(3, 4);
System.out.println(vector);
System.out.println(vector.search(6));
System.out.println(vector.search(7));
System.out.println(vector.search(8));
}
}
复杂度
含N个关键码的M阶B-树,最大高度(每个内部节点包含的关键码数尽可能少)为: O ( l o g m N ) O(log_mN) O(logmN)
最小树高(每个内部节点包含的关键码尽可能多)为: Ω ( l o g m N ) \Omega(log_mN) Ω(logmN)
其中一个表示上界,一个表示下界,因此说明B-树高度基本不会发生变化。