尼尧的算法日记：相交链表/环形链表（LeetCode 160/141）

都说不会算法的只能算是个CRUD工具人，而学会算法，不仅能提高解题思路，培养逻辑思维，也是提高自己的必经之路。

况且要去中大型公司，笔试总免不了手撕算法题。

本系列将把自己解题的过程和思路记录下来，也是提高自己算法能力的一种方式。

---

相交链表/环形链表的情形

• 相交链表

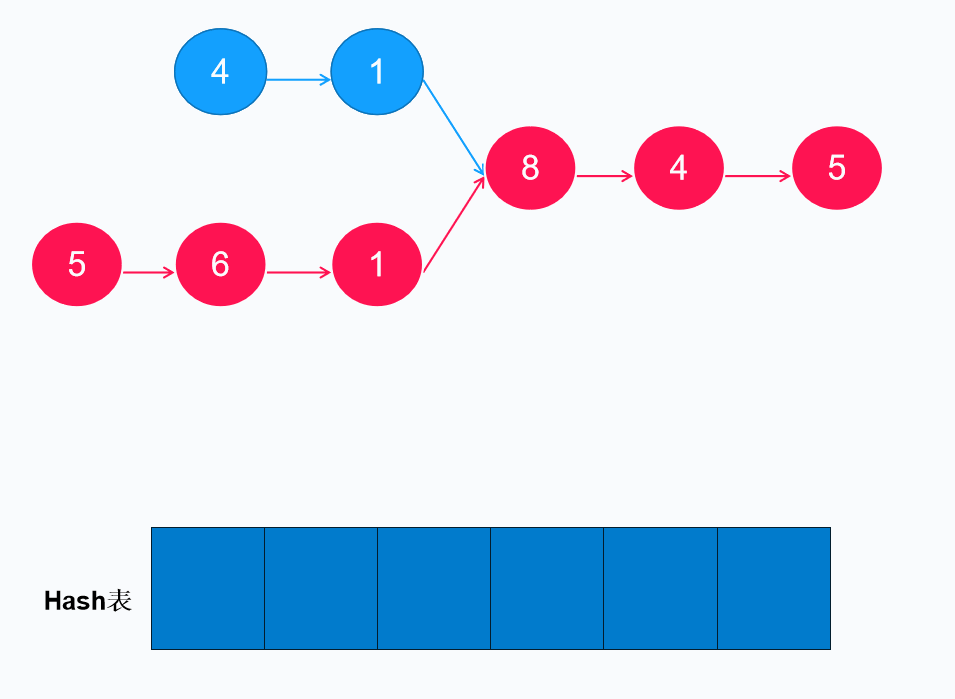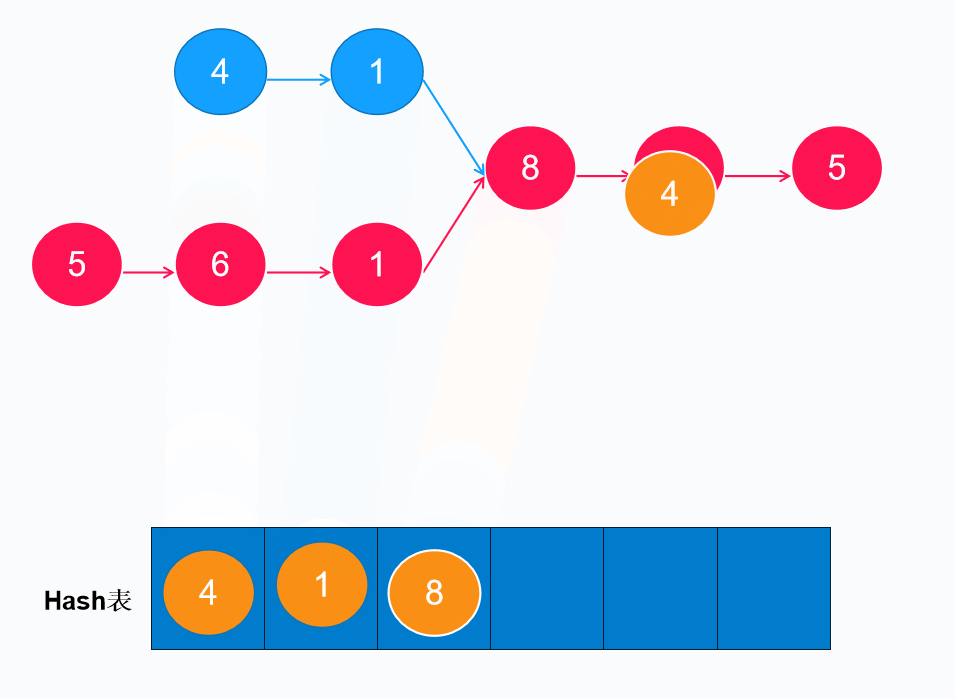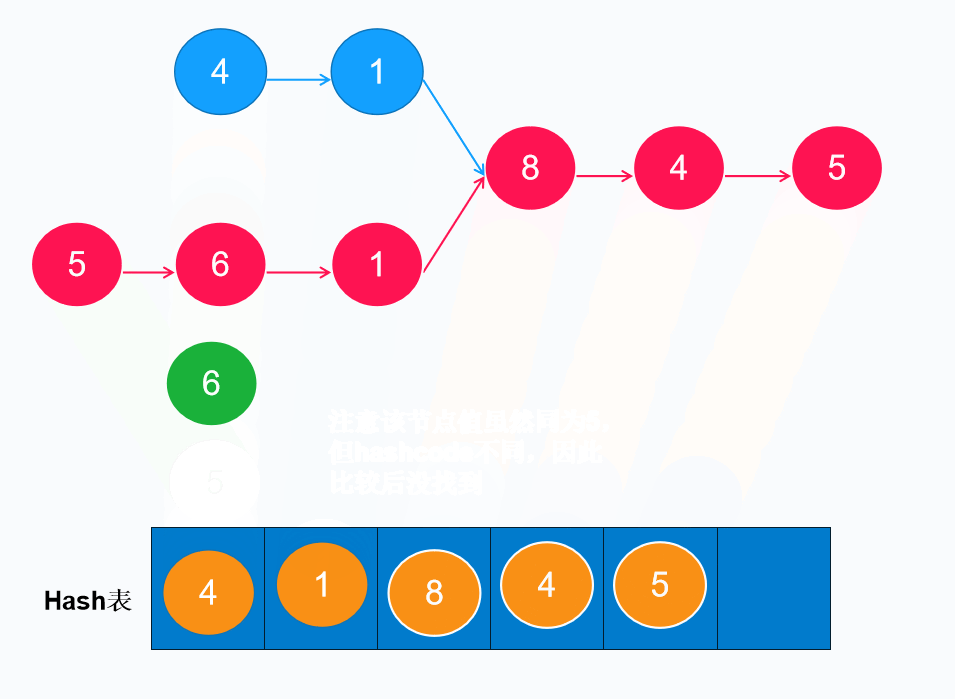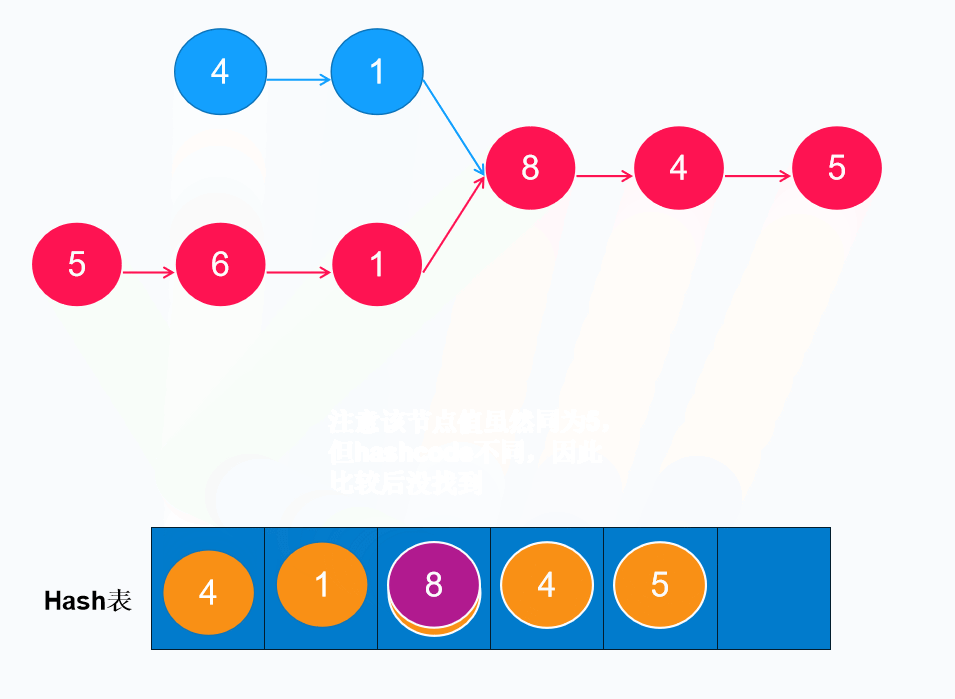
以下为单链链表存在相交的实例，编写一个程序，找到两个单链表相交的起始节点。（LeetCode.160 相交链表）

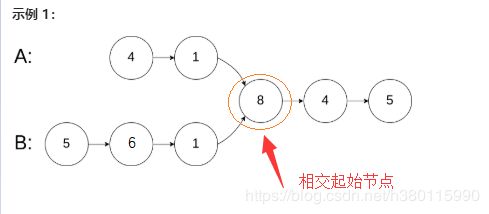
• 环形链表

存在单链表中尾部节点接到链表中某个节点，形成环状，写一个程序判断是否存在环。（LeetCode.141 环形链表）

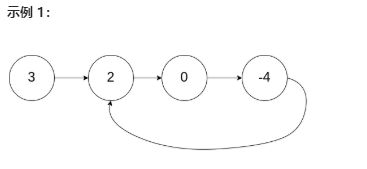
解题思路

这两道题难度系数都是简单。

他们存在共通性，都可以用Hash表法解出。

然后也可以用双指针法，但是他们的双指针法有一点区别。

Hash表法

Hash表法的思想是利用Hash运算的原理，将引用/地址存在Hash上，由于Hash运算的特性，对已经存在对象的引用进行比较，即可得出结果。

我们这里可以用HashMap/HashSet来做个辅助，HashSet底层其实就是HashMap（将实际值存在key上，value上存PRESENT对象，由于key相等就会覆盖，就保证了元素不重复）。

来看看HashMap的Hash函数；

static final int hash(Object key) {
        int h;
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
        //即key.hashCode() ^ (key.hashCode()>>>16)
    }

其中 ^ 即异或运算，>>> 右移运算，它们两个都是二进制的位运算。

十进制转换为二级制：给定的数循环除以2，直到商为0或者1为止。将每一步除的结果的余数记录下来，然后反过来就得到相应的二进制了。

举个栗子：  11 的 二进制为 1011
11/2 = 5  余1
5/2 = 2 余1
2/2 = 1 余0
1/2 = 0 余1
即二进制等于余数倒过来：1011

- 位异或运算（^）
运算规则是：两个数转为二进制，然后从高位开始比较，如果相同则为0，不相同则为1。

举栗子：2^11 = 9
2的二进制：10   11的二进制：1011 
   0010
 ^ 1011
 = 1001 = 9(十进制）

java中有三种移位运算符

<< : 左移运算符，num << 1,左移一位相当于num乘以2
>> : 右移运算符，num >> 1,右移一位相当于num除以2
>>> : 无符号右移，忽略符号位，空位都以0补齐

>> 与 >>> 的区别是，>>是带符号位的移动，>>>是补0的移动
举个栗子： 8>>1 = 4
8的二进制：1000  右移一位：100  即 4（十进制）
System.out.println(Integer.toBinaryString(-1));
//-1>>16输出也相同，因为带着1这个符号位移动，左边一直补的1
//11111111111111111111111111111111
System.out.println(Integer.toBinaryString(-1>>>16));
//1111111111111111

**普及了以上的知识，我们回到正题。**由于Hash 的特性，所以我们可以用它先存储对象的地址，当进入环状（相交节点）时，由于hashcode（引用）不同，就能进行判断了。

首先对节点有个定义，定义节点对象为ListNode：

public class ListNode {
    public int value;
    public ListNode next;
    public ListNode(int x, ListNode next) {
        this.value = x;
        this.next = next;
    }
}

然后是Hash表法的解题方法：

//LeetCode.160 相交链表，返回两个链表中首个的相交头节点。
//时间复杂度 : O(m+n)，空间复杂度 : O(m) 或 O(n)
 public ListNode getIntersectionNodeByHash(ListNode headA, ListNode headB){
        Map nodes = new HashMap();
        //HashSet nodes = new HashSet();//也可以用HashSet
        ListNode A = headA;
        ListNode B = headB;
        while (A!= null){
            nodes.put(A, 0);
            A = A.next;
        }
        while (B != null){
            //hashmap的key是根据hash运算后进行存放，那么第一个5的ListNode在hash计算后是不存在的
            if(nodes.containsKey(B)){
            	//hashSet底层为HashMap，实际上是把值存在key上保证了值的不重复，key由于hash运算所以无序
            	//nodes.contains(B)
                return B;
            }else{
                B = B.next;
            }
        }
        return null;
    }

public static void main(String[] args) {
        ListNode n8 = new ListNode(5, null);
        ListNode n7 = new ListNode(4, n8);
        ListNode n6 = new ListNode(8, n7);
        
        ListNode n5 = new ListNode(1, n6);
        ListNode n4 = new ListNode(4, n5);
        
        ListNode n3 = new ListNode(1, n6);
        ListNode n2 = new ListNode(6, n3);
        ListNode n1 = new ListNode(5, n2);
        System.out.println(getIntersectionNode.getIntersectionNodeByHash(n1, n4).value);
}

图解：

//LeetCode.141 环形链表,判断该链表是否有环
时间复杂度 : O(n)，空间复杂度 : O(n)
 public boolean hasCycleByHash(ListNode head) {
        Set<ListNode> nodes = new HashSet<>();
        while (head != null) {
            if (nodes.contains(head)) {
                return true;
            } else {
                nodes.add(head);
            }
            head = head.next;
        }
        return false;
    }

原理类似，不再重复作出动图了。

---

相交链表的双指针法（相交消除法）

相交消除法的思想是以时间换空间，仅使用O(1)的空间解决。

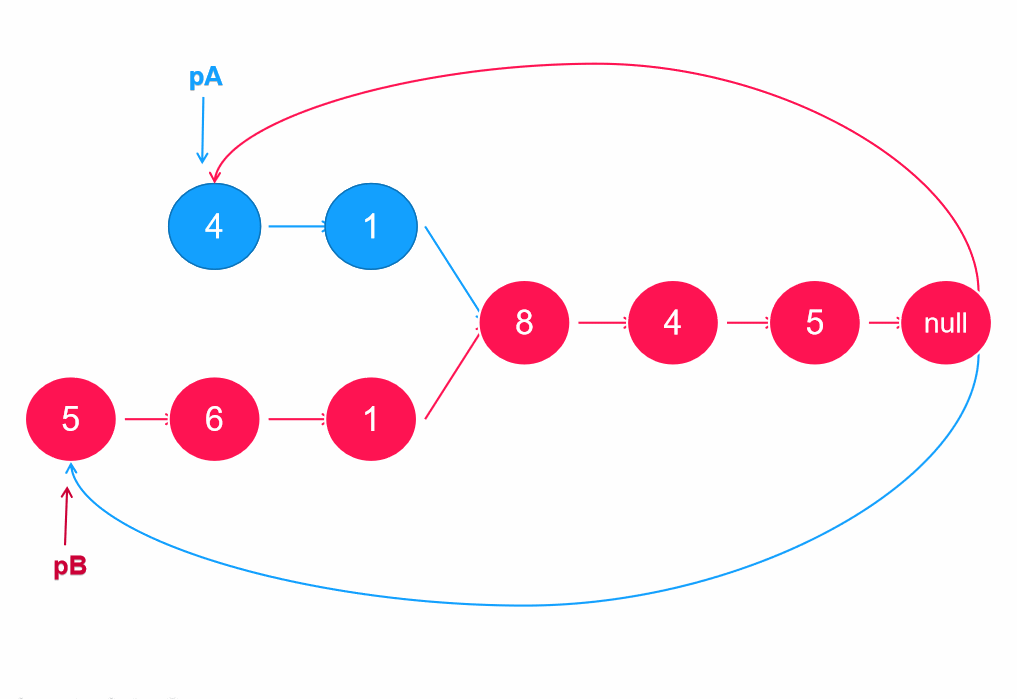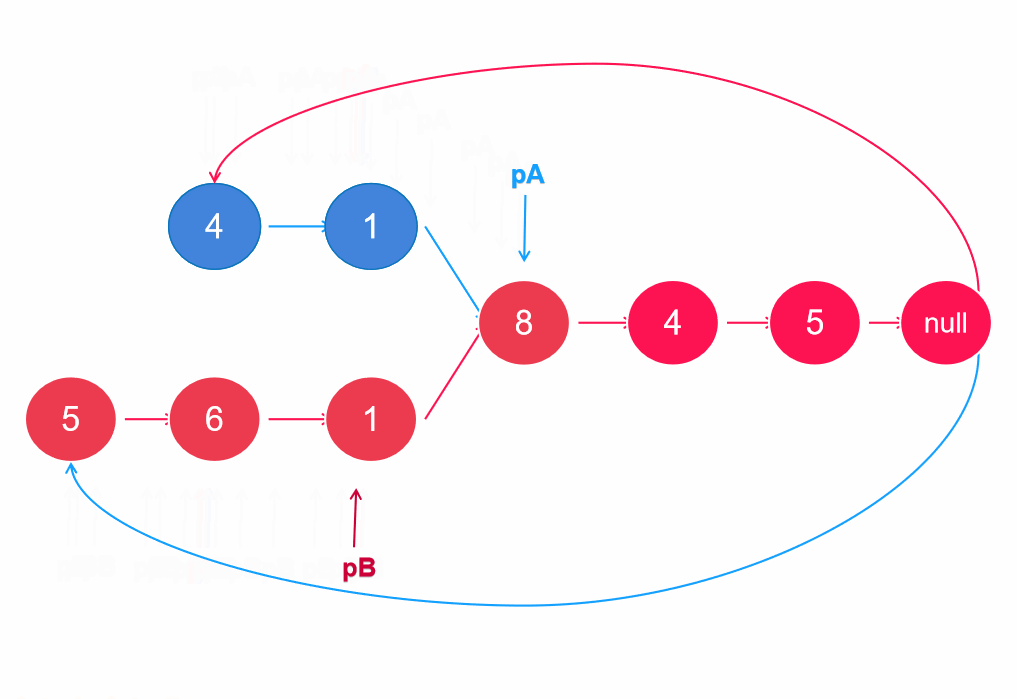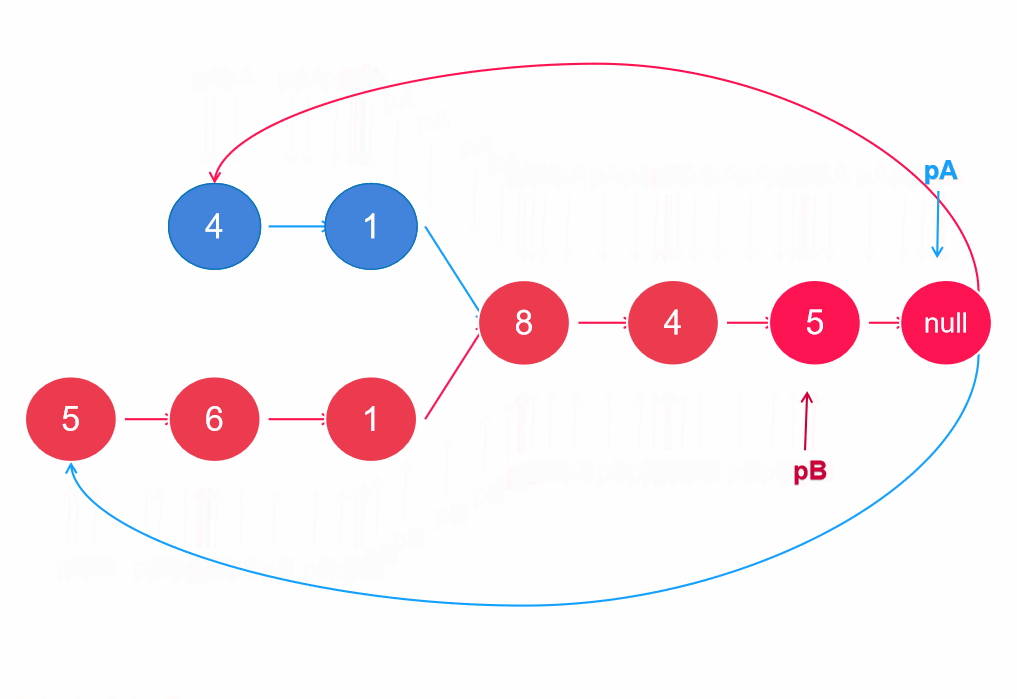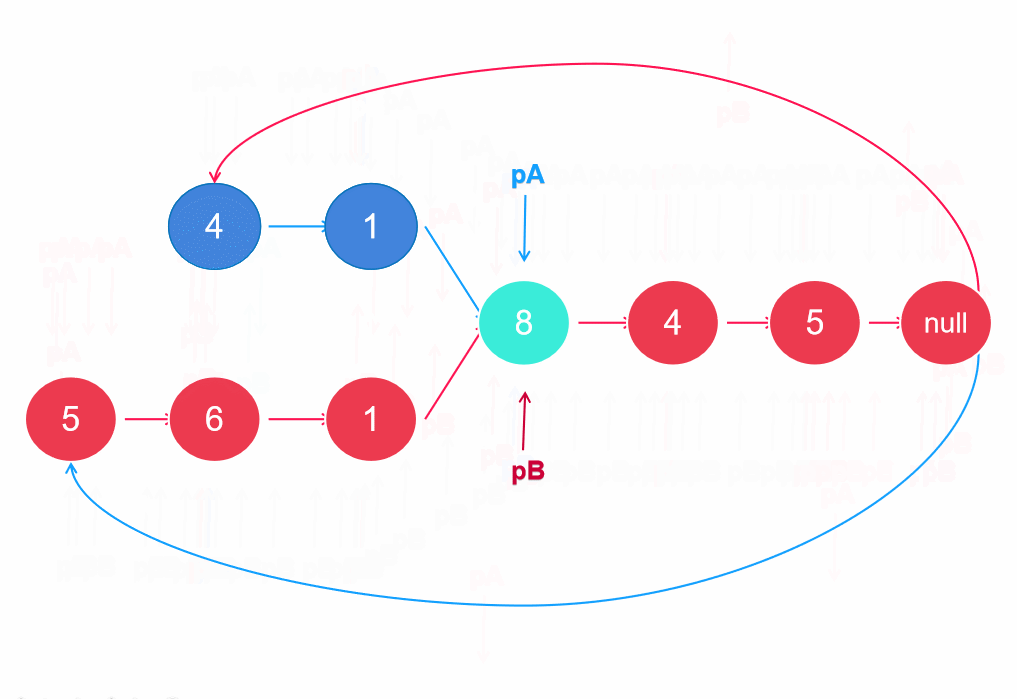
它的原理是设置指针遍历到链表尾部，当next指向null时，又从另一条的链表头进行遍历，则两个指针肯定会有相遇的时候。因为A+B = B+A，当两个指针走过的长度一致时，自然会相遇。若没有相交节点，则最后相遇在null处。

//LeetCode.160 相交链表相交消除法 空间复杂度 O(1) 时间复杂度为 O(m+n)
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) return null;
        ListNode pA = headA, pB = headB;
        while (pA != pB) {
            // if(pA==null)pA = headB else pA.next 若不相交，因为会先走到null的下一次才会指向头结点，
            // 所有当A+B都走完的最后一次共同指向null是返回null，不会死循环
            pA = pA == null ? headB : pA.next;
            pB = pB == null ? headA : pB.next;
        }
        return pA;
    }

图解：

---

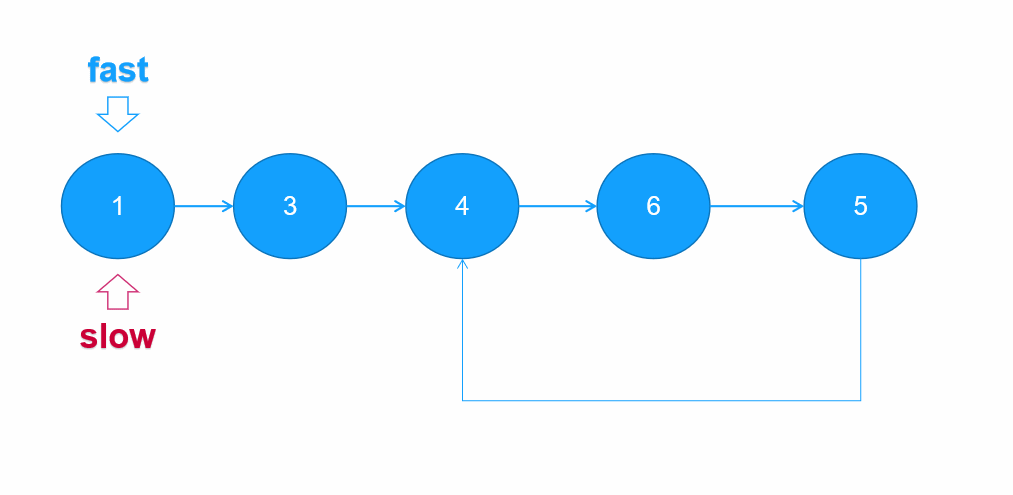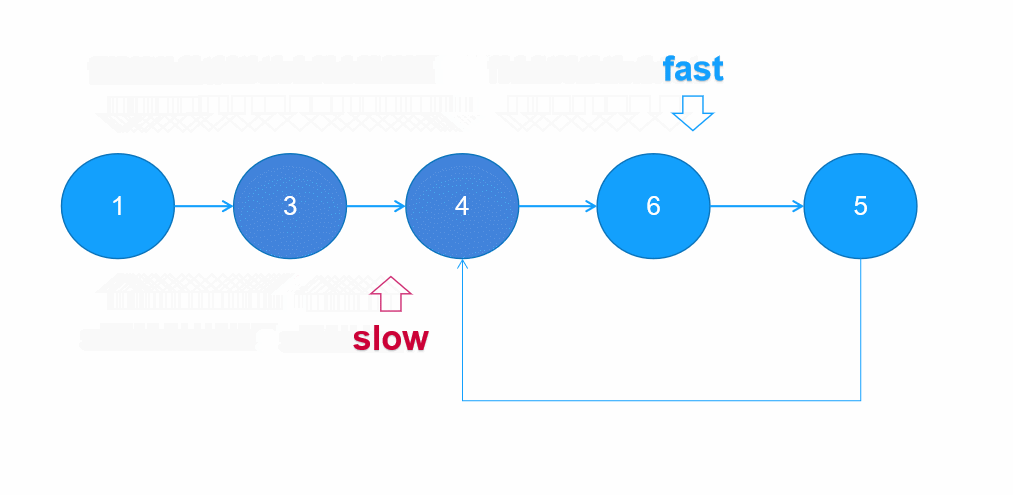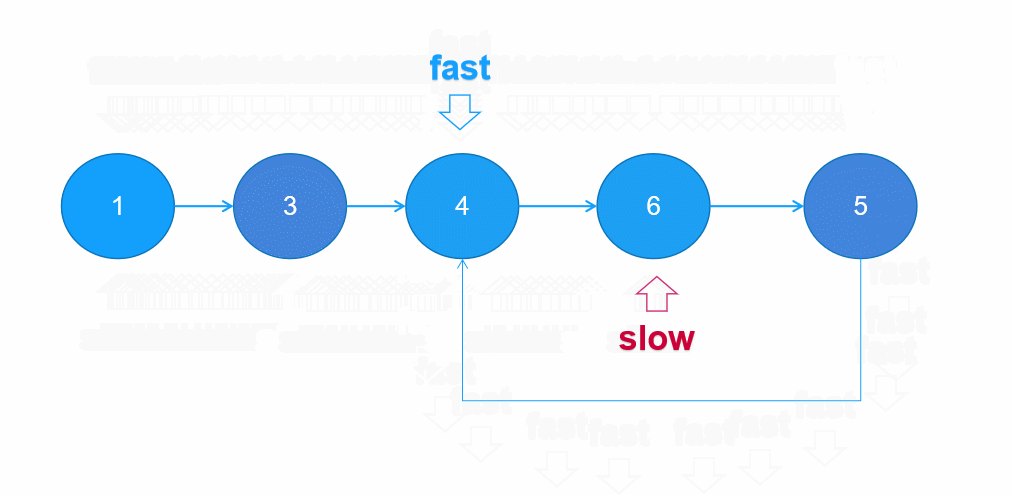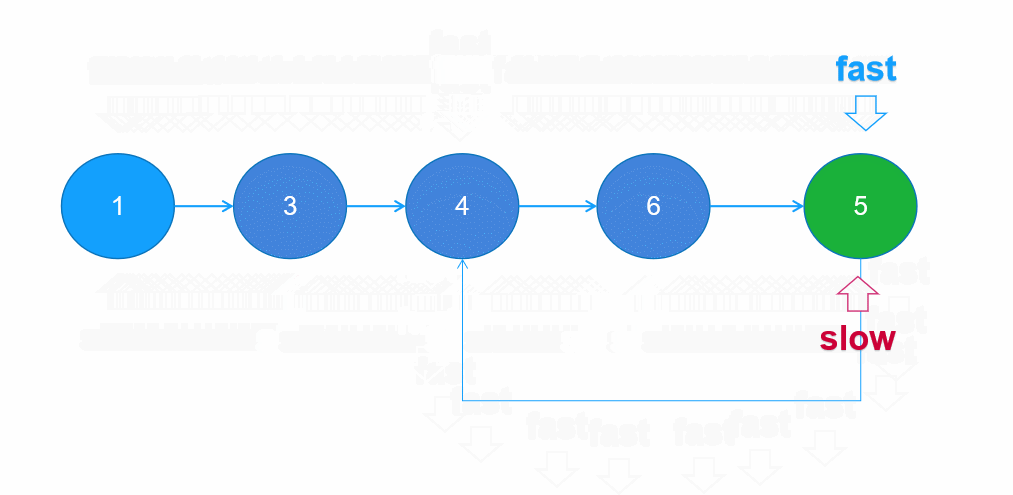
环形链表双指针法（快慢指针法）

快慢指针法的思想是设置两个指针，一个快一个慢，快指针每次向前移动2步，慢指针每次向前移动1步，若存在环形的话，快指针迟早会与慢指针相遇。若不存在环，快指针将会先走到null。

//LeetCode.141 环形链表 快慢指针法 空间复杂度 O(1) 时间复杂度为 O(n)
public boolean hasCycle(ListNode head) {
        if (head == null || head.next == null) {
            return false;
        }
        ListNode fast = head;
        ListNode slow = head;
        while (fast != slow){
            if (fast == null || fast.next == null) {
                return false;
            }
            fast = fast.next.next;
            slow = slow.next;
        }
        return true;
    }

图解：

---

本文参考：
[1] @LeetCode官网：160.相交链表 题解
[2] @LeetCode官网：141.环形链表 题解