前言
这篇郭先生就来说说欧拉角和四元数,欧拉角和四元数的优缺点是老生常谈的话题了,使用条件我就不多说了,我只说一下使用方法。
1. 欧拉角(Euler)
欧拉角描述一个旋转变换,通过指定轴顺序和其各个轴向上的指定旋转角度来旋转一个物体。下面我们开看看它的方法
1. set( x: number, y: number, z: number, order?: string ): Euler
x - 用弧度表示x轴旋转量。y - 用弧度表示y轴旋转量。z - 用弧度表示z轴旋转量。order - (optional) 表示旋转顺序的字符串。设置该欧拉变换的角度和旋转顺序 order。
2. clone(): this
返回一个与当前参数相同的新欧拉角。
3. copy( euler: Euler ): this
将 euler 的属性拷贝到当前对象。
4. setFromRotationMatrix( m: Matrix4, order?: string ): Euler
m - Matrix4 矩阵上面的3x3部分是一个纯旋转矩阵rotation matrix (也就是不发生缩放)order - (可选参数) 表示旋转顺序的字符串。使用基于 order 顺序的纯旋转矩阵来设置当前欧拉角。
var vector = new THREE.Vector3(0,0,1);
var matrix = new THREE.Matrix4().makeRotationAxis(vector, Math.PI/6)
var euler = new THREE.Euler().setFromRotationMatrix(matrix); // 返回Euler {_x: -0, _y: 0, _z: 0.5235987755982987, _order: "XYZ"}
5. setFromQuaternion( q: Quaternion, order?: string ): Euler
根据 order 指定的方向,使用归一化四元数设置这个欧拉变换的角度。
var vector = new THREE.Vector3(0,0,1);
var quaternion = new THREE.Quaternion().setFromAxisAngle(vector, Math.PI/6)
var euler = new THREE.Euler().setFromQuaternion(quaternion);// 返回Euler {_x: -0, _y: 0, _z: 0.5235987755982987, _order: "XYZ"}结果同上
6. setFromVector3( v: Vector3, order?: string ): Euler
设置 x, y and z 并且选择性更新 order。
var vector = new THREE.Vector3(0,0,Math.PI/6);
var euler = new THREE.Euler().setFromVector3(vector);/ 返回Euler {_x: -0, _y: 0, _z: 0.5235987755982987, _order: "XYZ"}结果同上
7. reorder( newOrder: string ): Euler
通过这个欧拉角创建一个四元数,然后用这个四元数和新顺序设置这个欧拉角。
8. equals( euler: Euler ): boolean
检查 euler 是否与当前对象相同。
9. fromArray( xyzo: any[] ): Euler
长度为3或4的一个 array 。array[3] 是一个可选的 order 参数。将欧拉角的x分量设置为 array[0]。将欧拉角的x分量设置为 array[1]。将欧拉角的x分量设置为 array[2]。将array[3]设置给欧拉角的 order 。可选。
10. toArray( array?: number[], offset?: number ): number[]
返回一个数组:[x, y, z, order ]。
11. toVector3( optionalResult?: Vector3 ): Vector3
以 Vector3 的形式返回欧拉角的 x, y 和 z。
var vector = new THREE.Vector3(0,0,Math.PI/6);
var euler = new THREE.Euler().setFromVector3(vector);
euler.toVector3(); //返回Vector3 {x: 0, y: 0, z: 0.5235987755982988}
2. 四元数
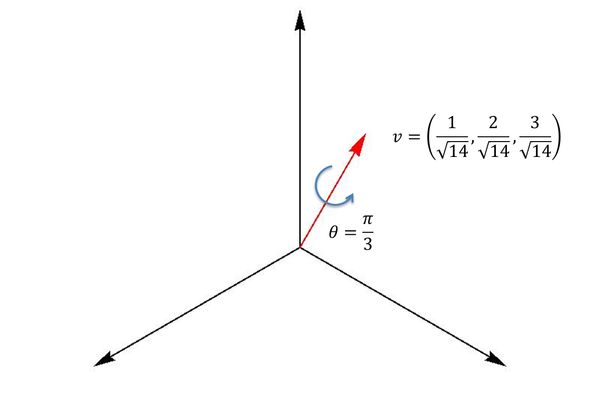
四元数对象Quaternion使用x、y、z和w四个分量表示。在三维空间中一个旋转由一个旋转轴、一个旋转角度和旋转方向来唯一确定。
假设我们默认为右手法则的旋转,则旋转方向为逆时针,旋转轴向量为v = (vx, vy, vz), 角度为旋转角度,那么该旋转就应该类似如下图所示:
其对应的四元数就是:
1. set( x: number, y: number, z: number, w: number ): Quaternion
设置该四元数的值。
2. clone(): this
克隆此四元数。
3. copy( q: Quaternion ): this
将q的值复制到这个四元数。
4. setFromEuler( euler: Euler ): Quaternion
用欧拉角指定的旋转来设置此四元数。
var euler = new THREE.Euler(0,0,Math.PI/6);
var quaternion = new THREE.Quaternion().setFromEuler(euler) //返回Quaternion {_x: 0, _y: 0, _z: 0.25881904510252074, _w: 0.9659258262890683}
5. setFromAxisAngle( axis: Vector3, angle: number ): Quaternion
使用由轴和角度指定的旋转来设置此四元数。axis 应该是归一化的,angle 的单位是弧度。
var vector1 = new THREE.Vector3(0,0,1);
var vector2 = new THREE.Vector3(0,0,2);
var quaternion1 = new THREE.Quaternion().setFromAxisAngle(vector1, Math.PI/6); //返回Quaternion {_x: 0, _y: 0, _z: 0.25881904510252074, _w: 0.9659258262890683}
var quaternion2 = new THREE.Quaternion().setFromAxisAngle(vector2, Math.PI/6); //返回Quaternion {_x: 0, _y: 0, _z: 0.5176380902050415, _w: 0.9659258262890683}
可见axis是否归一化对四元数的x、y和z值的影响是线性的。
6. setFromRotationMatrix( m: Matrix4 ): Quaternion
从m的旋转分量来设置该四元数。使用很简单就不多说了。
7. setFromUnitVectors( vFrom: Vector3, vTo: Vector3 ): Quaternion
通过从向量vFrom到vTo所需的旋转来设置这四元数。vFrom 和 vTo 应该是归一化的。我们来看一下
var vector1 = new THREE.Vector3(1,1,0); var vector2 = new THREE.Vector3(0,1,0); var quaternion = new THREE.Quaternion().setFromUnitVectors(vector1, vector2); //相当于绕z轴旋转了Math.PI/4
8. angleTo( q: Quaternion ): number
返回这个四元数到q的角度
var quaternion1 = new THREE.Quaternion().setFromEuler(new THREE.Euler(0,0,Math.PI/3)); var quaternion2 = new THREE.Quaternion().setFromEuler(new THREE.Euler(0,0,Math.PI/6)); quaternion1.angleTo(quaternion2); // 返回0.5235987755982987
9. rotateTowards( q: Quaternion, step: number ): Quaternion
将此四元数按给定的step旋转到定义的四元数q。该方法确保最终四元数不会超出q。那么是什么意思呢?
var quaternion1 = new THREE.Quaternion().setFromEuler(new THREE.Euler(0,0,Math.PI/3)); //{_x: 0, _y: 0, _z: 0.49999999999999994, _w: 0.8660254037844387}
var quaternion2 = new THREE.Quaternion().setFromEuler(new THREE.Euler(0,0,Math.PI/6)); //{_x: 0, _y: 0, _z: 0.25881904510252074, _w: 0.9659258262890683}
quaternion1.rotateTowards( quaternion2, 0); //{_x: 0, _y: 0, _z: 0.49999999999999994, _w: 0.8660254037844387}
quaternion1.rotateTowards( quaternion2, 0.5); //{_x: 0, _y: 0, _z: 0.2701980971440553, _w: 0.9628047508709812}
quaternion1.rotateTowards( quaternion2, 1); //{_x: 0, _y: 0, _z: 0.25881904510252074, _w: 0.9659258262890683}
可以看出其内部使用了quaternion.slerp()方法。当step为0时,rotateTowards方法返回就是当前四元数。当step为1时,rotateTowards方法返回就是参数q的四元数。当step为0~1之间时,rotateTowards方法返回就是当前四元数和参数q的四元数之间的插值。
10. inverse(): Quaternion
转置此四元数-计算共轭。假设四元数具有单位长度。
var quaternion = new THREE.Quaternion().setFromEuler(new THREE.Euler(Math.PI/6,Math.PI/6,Math.PI/6)); //初始四元数Quaternion {_x: 0.30618621784789724, _y: 0.17677669529663687, _z: 0.30618621784789724, _w: 0.8838834764831845}
quaternion.inverse(); //返回Quaternion {_x: -0.30618621784789724, _y: -0.17677669529663687, _z: -0.30618621784789724, _w: 0.8838834764831845}
由此可知计算共轭之后,x、y和z分别取复制,而w值不变。
11. conjugate(): Quaternion
返回此四元数的旋转共轭。四元数的共轭。表示旋转轴在相反方向上的同一个旋转。经过我的测试这个方法和inverse()方法是一样的,来看看inverse的源码
inverse: function () {
// quaternion is assumed to have unit length
return this.conjugate();
},
12. dot( v: Quaternion ): number
计算四元数v和当前四元数的点积。众所周知点积得到的是一个数字。很简单
13. lengthSq(): number
计算四元数的平方长度。就是各个值平方求和。
14 length(): number
计算此四元数的长度。也就是各个值平方求和,然后在开根号。
15. normalize(): Quaternion
归一化该四元数。开看下源码
normalize: function () {
var l = this.length();
if ( l === 0 ) { //如果四元数参length为0,那么this._x、this._y和this._z都设置为0,this._w设置为1
this._x = 0;
this._y = 0;
this._z = 0;
this._w = 1;
} else { //如果四元数参length为l,那么四元数的各个参数乘以l的倒数。
l = 1 / l;
this._x = this._x * l;
this._y = this._y * l;
this._z = this._z * l;
this._w = this._w * l;
}
return this;
},
16. multiply( q: Quaternion ): Quaternion
把该四元数和q相乘。具体怎么相乘。稍后再说。
17. premultiply( q: Quaternion ): Quaternion;
使用q左乘以(pre-multiply)该四元数。同样稍后再说。
18. multiplyQuaternions( a: Quaternion, b: Quaternion ): Quaternion
四元数a乘以四元数b,我们说一下四元数的乘法。
multiplyQuaternions: function ( a, b ) {
var qax = a._x, qay = a._y, qaz = a._z, qaw = a._w;
var qbx = b._x, qby = b._y, qbz = b._z, qbw = b._w;
this._x = qax * qbw + qaw * qbx + qay * qbz - qaz * qby;
this._y = qay * qbw + qaw * qby + qaz * qbx - qax * qbz;
this._z = qaz * qbw + qaw * qbz + qax * qby - qay * qbx;
this._w = qaw * qbw - qax * qbx - qay * qby - qaz * qbz;
return this;
},
19. equals( v: Quaternion ): boolean;
比较v和这个四元数的各个分量,以确定两者是否代表同样的旋转。不多说。
20. slerp( qb: Quaternion, t: number ): Quaternion
处理四元数之间的球面线性插值。t 代表quaternionA(这里t为0)和quaternionB(这里t为1)这两个四元数之间的旋转量。quaternion 被设置为结果。rotateTowards的底层同样使用了slerp方法。
var quaternion1 = new THREE.Quaternion().setFromEuler(new THREE.Euler(0,0,Math.PI/6));
var quaternion2 = new THREE.Quaternion().setFromEuler(new THREE.Euler(0,0,Math.PI/2));
quaternion1; //quaternion1的值为{_x: 0, _y: 0, _z: 0.25881904510252074, _w: 0.9659258262890683}
quaternion2; //quaternion2的值为{_x: 0, _y: 0, _z: 0.7071067811865475, _w: 0.7071067811865476}
quaternion1.slerp(quaternion2, 0) //返回的结果和quaternion1相同
quaternion1.slerp(quaternion2, 1) //返回的结果和quaternion2相同
quaternion1.slerp(quaternion2, 其他值) //返回quaternion1到quaternion2的插值,当然这个t也是可以大于1的
//看一下rotateTowards的部分源码
rotateTowards: function ( q, step ) {
var angle = this.angleTo( q );
if ( angle === 0 ) return this;
var t = Math.min( 1, step / angle );
this.slerp( q, t );
return this;
}
21. static slerp: functistatic slerp(qa: Quaternion, qb: Quaternion, qm: Quaternion, t: number): Quaternionon
这是slerp的静态方法,无需动态设置。同样使用了slerp方法。
slerp: function ( qa, qb, qm, t ) {
return qm.copy( qa ).slerp( qb, t );
}
关于欧拉角四元数要说的差不多就这些,还需要平时多多应用才能记熟。
总结
到此这篇关于three.js欧拉角和四元数的使用方法的文章就介绍到这了,更多相关three.js欧拉角和四元数内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!