python版本选择
这里选的python版本是2.7,因为我之前用python3试了几次,发现在画3d图的时候会报错,所以改用了2.7。
数据集选择
数据集我选了一个包含两个变量,三个参数的数据集,这样可以画出3d图形对结果进行验证。
部分函数总结
symbols()函数:首先要安装sympy库才可以使用。用法:
>>> x1 = symbols('x2')
>>> x1 + 1
x2 + 1
在这个例子中,x1和x2是不一样的,x2代表的是一个函数的变量,而x1代表的是python中的一个变量,它可以表示函数的变量,也可以表示其他的任何量,它替代x2进行函数的计算。实际使用的时候我们可以将x1,x2都命名为x,但是我们要知道他们俩的区别。
再看看这个例子:
>>> x = symbols('x')
>>> expr = x + 1
>>> x = 2
>>> print(expr)
x + 1
作为python变量的x被2这个数值覆盖了,所以它现在不再表示函数变量x,而expr依然是函数变量x+1的别名,所以结果依然是x+1。
subs()函数:既然普通的方法无法为函数变量赋值,那就肯定有函数来实现这个功能,用法:
>>> (1 + x*y).subs(x, pi)#一个参数时的用法
pi*y + 1
>>> (1 + x*y).subs({x:pi, y:2})#多个参数时的用法
1 + 2*pi
diff()函数:求偏导数,用法:result=diff(fun,x),这个就是求fun函数对x变量的偏导数,结果result也是一个变量,需要赋值才能得到准确结果。
代码实现:
from __future__ import division
from sympy import symbols, diff, expand
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data = {'x1': [100, 50, 100, 100, 50, 80, 75, 65, 90, 90],
'x2': [4, 3, 4, 2, 2, 2, 3, 4, 3, 2],
'y': [9.3, 4.8, 8.9, 6.5, 4.2, 6.2, 7.4, 6.0, 7.6, 6.1]}#初始化数据集
theta0, theta1, theta2 = symbols('theta0 theta1 theta2', real=True) # y=theta0+theta1*x1+theta2*x2,定义参数
costfuc = 0 * theta0
for i in range(10):
costfuc += (theta0 + theta1 * data['x1'][i] + theta2 * data['x2'][i] - data['y'][i]) ** 2
costfuc /= 20#初始化代价函数
dtheta0 = diff(costfuc, theta0)
dtheta1 = diff(costfuc, theta1)
dtheta2 = diff(costfuc, theta2)
rtheta0 = 1
rtheta1 = 1
rtheta2 = 1#为参数赋初始值
costvalue = costfuc.subs({theta0: rtheta0, theta1: rtheta1, theta2: rtheta2})
newcostvalue = 0#用cost的值的变化程度来判断是否已经到最小值了
count = 0
alpha = 0.0001#设置学习率,一定要设置的比较小,否则无法到达最小值
while (costvalue - newcostvalue > 0.00001 or newcostvalue - costvalue > 0.00001) and count < 1000:
count += 1
costvalue = newcostvalue
rtheta0 = rtheta0 - alpha * dtheta0.subs({theta0: rtheta0, theta1: rtheta1, theta2: rtheta2})
rtheta1 = rtheta1 - alpha * dtheta1.subs({theta0: rtheta0, theta1: rtheta1, theta2: rtheta2})
rtheta2 = rtheta2 - alpha * dtheta2.subs({theta0: rtheta0, theta1: rtheta1, theta2: rtheta2})
newcostvalue = costfuc.subs({theta0: rtheta0, theta1: rtheta1, theta2: rtheta2})
rtheta0 = round(rtheta0, 4)
rtheta1 = round(rtheta1, 4)
rtheta2 = round(rtheta2, 4)#给结果保留4位小数,防止数值溢出
print(rtheta0, rtheta1, rtheta2)
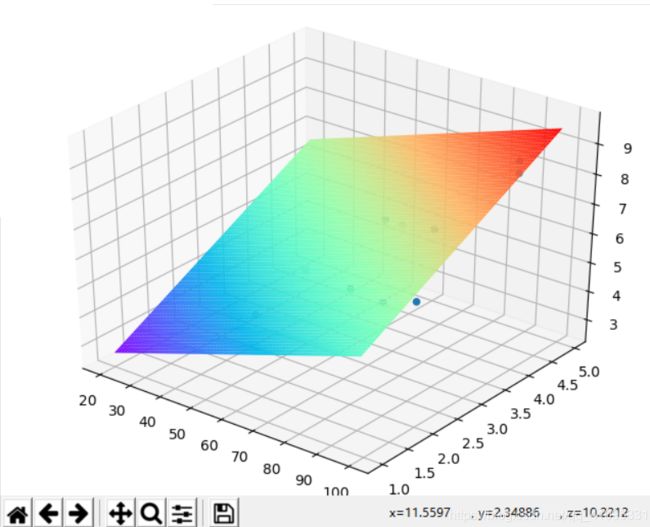
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(data['x1'], data['x2'], data['y']) # 绘制散点图
xx = np.arange(20, 100, 1)
yy = np.arange(1, 5, 0.05)
X, Y = np.meshgrid(xx, yy)
Z = X * rtheta1 + Y * rtheta2 + rtheta0
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'))
plt.show()#绘制3d图进行验证
结果:
实例扩展:
'''
梯度下降算法
Batch Gradient Descent
Stochastic Gradient Descent SGD
'''
__author__ = 'epleone'
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sys
# 使用随机数种子, 让每次的随机数生成相同,方便调试
# np.random.seed(111111111)
class GradientDescent(object):
eps = 1.0e-8
max_iter = 1000000 # 暂时不需要
dim = 1
func_args = [2.1, 2.7] # [w_0, .., w_dim, b]
def __init__(self, func_arg=None, N=1000):
self.data_num = N
if func_arg is not None:
self.FuncArgs = func_arg
self._getData()
def _getData(self):
x = 20 * (np.random.rand(self.data_num, self.dim) - 0.5)
b_1 = np.ones((self.data_num, 1), dtype=np.float)
# x = np.concatenate((x, b_1), axis=1)
self.x = np.concatenate((x, b_1), axis=1)
def func(self, x):
# noise太大的话, 梯度下降法失去作用
noise = 0.01 * np.random.randn(self.data_num) + 0
w = np.array(self.func_args)
# y1 = w * self.x[0, ] # 直接相乘
y = np.dot(self.x, w) # 矩阵乘法
y += noise
return y
@property
def FuncArgs(self):
return self.func_args
@FuncArgs.setter
def FuncArgs(self, args):
if not isinstance(args, list):
raise Exception(
'args is not list, it should be like [w_0, ..., w_dim, b]')
if len(args) == 0:
raise Exception('args is empty list!!')
if len(args) == 1:
args.append(0.0)
self.func_args = args
self.dim = len(args) - 1
self._getData()
@property
def EPS(self):
return self.eps
@EPS.setter
def EPS(self, value):
if not isinstance(value, float) and not isinstance(value, int):
raise Exception("The type of eps should be an float number")
self.eps = value
def plotFunc(self):
# 一维画图
if self.dim == 1:
# x = np.sort(self.x, axis=0)
x = self.x
y = self.func(x)
fig, ax = plt.subplots()
ax.plot(x, y, 'o')
ax.set(xlabel='x ', ylabel='y', title='Loss Curve')
ax.grid()
plt.show()
# 二维画图
if self.dim == 2:
# x = np.sort(self.x, axis=0)
x = self.x
y = self.func(x)
xs = x[:, 0]
ys = x[:, 1]
zs = y
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(xs, ys, zs, c='r', marker='o')
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
else:
# plt.axis('off')
plt.text(
0.5,
0.5,
"The dimension(x.dim > 2) \n is too high to draw",
size=17,
rotation=0.,
ha="center",
va="center",
bbox=dict(
boxstyle="round",
ec=(1., 0.5, 0.5),
fc=(1., 0.8, 0.8), ))
plt.draw()
plt.show()
# print('The dimension(x.dim > 2) is too high to draw')
# 梯度下降法只能求解凸函数
def _gradient_descent(self, bs, lr, epoch):
x = self.x
# shuffle数据集没有必要
# np.random.shuffle(x)
y = self.func(x)
w = np.ones((self.dim + 1, 1), dtype=float)
for e in range(epoch):
print('epoch:' + str(e), end=',')
# 批量梯度下降,bs为1时 等价单样本梯度下降
for i in range(0, self.data_num, bs):
y_ = np.dot(x[i:i + bs], w)
loss = y_ - y[i:i + bs].reshape(-1, 1)
d = loss * x[i:i + bs]
d = d.sum(axis=0) / bs
d = lr * d
d.shape = (-1, 1)
w = w - d
y_ = np.dot(self.x, w)
loss_ = abs((y_ - y).sum())
print('\tLoss = ' + str(loss_))
print('拟合的结果为:', end=',')
print(sum(w.tolist(), []))
print()
if loss_ < self.eps:
print('The Gradient Descent algorithm has converged!!\n')
break
pass
def __call__(self, bs=1, lr=0.1, epoch=10):
if sys.version_info < (3, 4):
raise RuntimeError('At least Python 3.4 is required')
if not isinstance(bs, int) or not isinstance(epoch, int):
raise Exception(
"The type of BatchSize/Epoch should be an integer number")
self._gradient_descent(bs, lr, epoch)
pass
pass
if __name__ == "__main__":
if sys.version_info < (3, 4):
raise RuntimeError('At least Python 3.4 is required')
gd = GradientDescent([1.2, 1.4, 2.1, 4.5, 2.1])
# gd = GradientDescent([1.2, 1.4, 2.1])
print("要拟合的参数结果是: ")
print(gd.FuncArgs)
print("===================\n\n")
# gd.EPS = 0.0
gd.plotFunc()
gd(10, 0.01)
print("Finished!")
到此这篇关于python实现梯度下降算法的实例详解的文章就介绍到这了,更多相关教你用python实现梯度下降算法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!