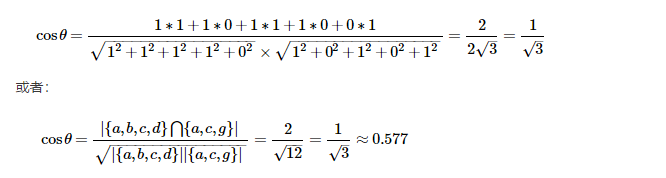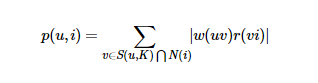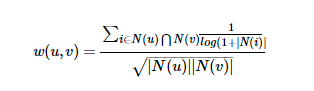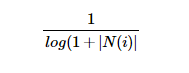推荐系统基础算法--余弦相似度算法详解及应用
一、简述
这几天在看《推荐系统实战》这本书。其中,基于领域的算法是推荐系统中最基本的算法,什么是基于领域的算法呢?简单来说就是基于用户(或物品)的协同过滤算法,所谓的协同的意思就是需要用户(或物品)共同参与。从而通过用户的行为,推荐和他兴趣相似的其他用户喜欢的物品或他自己之前喜欢的物品的相似的物品。这里有一个查找物品或用户兴趣的相似性,就是我们今天讨论的主题相似性的度量。
二、协同过滤算法
我们有时会遇到你的朋友向你询问:“我现在在学习XXX,能推荐什么专业的书籍吗?”,这个时候你一般都会给他一些推荐或建议,这其实就是一个个性化的推荐的例子。在这个例子中,你的朋友之所以会向你询问,最终做出决定。主要的原因还是你与他可能有共同的爱好或研究领域,并且信任你。那么,在一个在线的个性化推荐系统中,当一个用户A需要个性化推荐时,可以先找到和他有相似兴趣的其他用户,然后把那些用户喜欢的、且用户A没有看过的物品推荐给他。这种方法就是基于用户的协同过滤算法。总结一下主要包括两个步骤:
- 找到和目标用户兴趣相似的用户集合
- 找到这个集合中的用户喜欢的,且目标用户没有看到过的物品推荐给他
这里协同过滤算法主要是利用行为的相似度计算兴趣的相似度。
给定用户u和用户v,令N(u)表示用户u曾经有过行为(浏览或购买)的物品集合,令N(v)表示用户v曾经有过行为的物品集合。那么,我们可以给出简单的计算u与v兴趣相似度的公式:
关于第一个公式,我们可以理解为:用户u和v感兴趣的物品集合的交集,即两个用户都感兴趣的物品除以物品集合的并集,得到一个简单的相似度,例如:用户u感兴趣的物品集合是Nu={a,b,c,d},用户v感兴趣的物品集合Nv={a,c,g},那么:
Wuv={a,c}/{a,b,c,d,g}=2/5=0.4
第二个公式,稍复杂了点。我们先来看看这个公式是如何推导出来的,又有什么样的含义?
余弦相似度
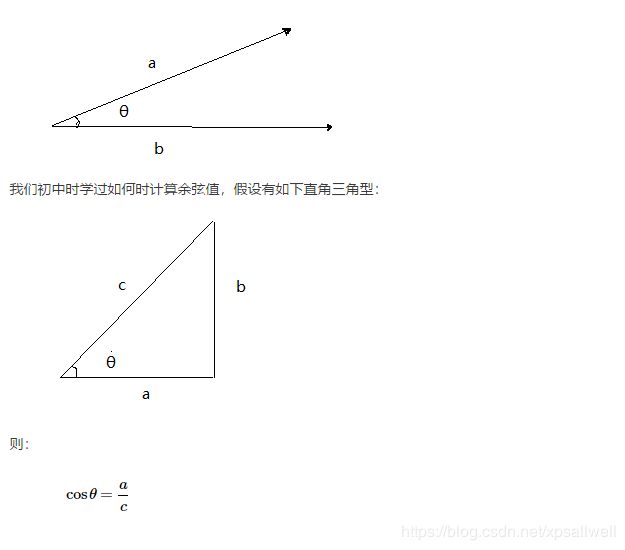
余弦相似度可以用向量空间中两个向量的夹角的余弦值为衡量这两个个体之间的差异大小,值越接近于1就表示夹角越接近于0,表示这两个个体的越相似,反之越接近于0则差异越大。这就是余弦相似性。
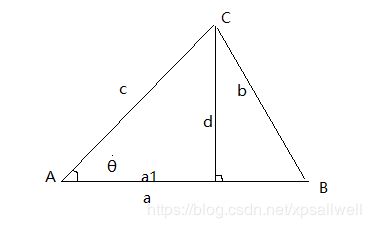
但是这个公式只适用于直角三角型,而对于一般的三角型,我们有公式:
推导过程:
对于一般的三角型ABC,d为高
所以,有:
再来看看,上面的例子,
Nu=X={a,b,c,d},Nv=Y={a,c,g},令物品出现一次就加1,就得到两个向量
X={1,1,1,1,0},Nv=Y={1,0,1,0,1},代入上式得:
从上面的计算得出,用户u与v的兴趣相似度是0.577,属于一般偏上一点,扩展一下,假设用户v也购买了商品d,那么,计算结果就是0.75了。
计算优化
上式是计算两两用户之间的相似度,它的时间复杂度是O(|U|*|U|),当用户量特别大的时候非常的耗时。事实上,在现实中很多用户相互之间并没有对相同的物品产生过行为,即交集为0,这种情况计算的结果都是没有关系。所以我们可以首先计算出交集不为0的用户对(u,v),然后再计算这些用户。
我们可以建立一个倒排表,对于每个物品都保存对该物品产生过行为的用户列表,令稀疏矩阵C(u,v)=|N(u)⋂N(v)|,那么,假设用户u和v同时属于倒排表中K个物品对应的用户列表,就有C(u,v)=K。从而要以扫描倒排表中每个物品对应的用户列表,将用户列表中的两两用户对应的C(u,v)加1,最终可以得到所有用户之间不为0的C(u,v)
上图上,建立的一个4x4的矩阵W,对于物品a,将W[A][B]和W[B][A]加1,对于物品b,将W[A][C]和W[C][A]加1,依次类推。完成后我们就得到了一个矩阵,这里W就是余弦的分子部分,然后除以分母就可以得到用户之间的相似度。
得到相似度后,UserCF(基于用户的协同推荐算法)就可以给用户推荐和他兴趣最相似的K个用户喜欢的物品。如下公式度量了UserCF算法中用户u对物品i的感兴趣程度:
其中,S(u,K)包含和用户u兴趣最接近的K个用户,N(i)是对物品i有过行为的用户集合,wuv是用户u和v的兴趣相似度,rvi代表用户v对物品i的兴趣,因为使用的是单一行为的隐反馈数据,所以所有的rvi=1。
我们选取K=3,用户A对物品c、e都没有过行为,可以推荐给A,此时,使用UserCF计算A对c、e两个物品的兴趣度是:
p(A,c)=w(AB)+w(AD),p(A,e)=w(AC)+w(AD),可以以此类推其它物品,选取兴趣度p最高的topN推荐给用户A。
关于,算法的性能和准确率测试,自行阅读这本书(内容有点多,不好输入。哈哈)
算法的改进
上面计算用户之间的兴趣相似度还是有点粗糙的,比如:两个用户都对<新华字典>有过行为,但这并不能说明他们的兴趣是一样的,因为大多数人都买过这件商品。但如果用户都买过《java语言编程思想》,那么就可以认为他们的兴趣有很大的相似之处。换句话说,两个用户对冷门的物品采取过同样的行为更能说明他们兴趣的相似度。所以可以改进上述的公式(称为User-IIF):
此公式,通过
惩罚了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响。
总结
面对现在信息过载的状况,要想让用户从海量的信息中较准确的找到自己的想到的东西,再或者用户自己不知道自己想要什么,那么,推荐系统就可以帮助用户了解他自己喜欢的东西,从而也为商家带来一定的商业价值,互利共赢!余弦相似度算法是推荐系统中协同过滤的基础算法,主要的思想是以两个向量的夹角的余弦值来衡量相似度,夹角越小说明两者方向越接近,也就表示越相似,反之则越不相似,更甚者,夹角为180度时,说明两者截然相反!协同过滤还有一种比较常用的是基于物品的协同过滤,这个下章再讲。