【算法导论】最大子数组问题

       在算法导论中，最大子数组问题是在股票买卖的背景下提出来的。显然，我们都希望可以在“低位买进，高位卖出”，这样获利是最多的。不过，其实这算法对于实际操作也没多大意义，因为，你根本不知道目前的价钱是高位，还是低位。或许可以用ML的方法去学习出未来一天股价大涨还是大跌的特征，就可以预测未来，实际上应该也有人尝试过。不过估计是学不到很好的特征的，毕竟影响因素太多了。

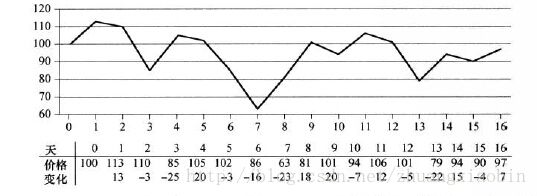
       例如下图放映了某只股票在17天内的股价变化，如果你可以在第7天之后买进，第11天卖出，那么收益是很可观的，可以达到43，在这17天内没有更好的组合来使得利益最大化了。

       要怎么求解这个问题呢？最直接的方法也是最暴力的方法--排列组合，把所有情况都拿去算一遍，然后把好的留下来。当然，问题是可以解决的，但是，复杂度太高了，是o（n^2）。换个角度，把每天的股价换成和前一天的差来组织数据，那么这么多天的数据其实就构成一个数组A，我们要的是找出这个数组A的一个子数组，这个子数组的和最大，这问题就叫做最大子数组（maximum subarray）问题。

       本文介绍一种高效的求解方法，来找到一个最大子数组。为什么强调“一个最大子数组”，因为有时候答案并不唯一。例如，股价连续几天一样，那么这些天里哪天买进都不影响结果。我们使用分治策略来求解这个问题。问什么要用分治算法，其实也就是为了降低复杂度。要在一个大数组找子数组，可以考虑两个长度更小的子数组中分别找到最大子数组，假如可以这两个子数组是可以连起来的，那么合起来就是答案了。下面理解一下下面的结论：

如果把数组A分成两个子数组A1和A2，A1=A[low,mid]，A2=A[mid+1,high]，其中low和high分别是A的最大和最小下标，mid=（low+high）/2，向上向下取整都一样，那么A[low,high]的任何子数组A[i,j]必然是以下三种情况之一：

（1）完全位于子数组A[low,mid]中,low<=i<=j<=mid；

（2）完全位于子数组A[mid+1,high]中,mid+1<=i<=j<=high；

（3）跨越了中点，因此low<=i；

       容易看到，如果把两个子数组继续分下去，就可以分成4个，然后是8个，一直分下去，直到low=i=j=high就不可可以再分了。把大问题分解成小问题求解，然后再把小问题的解合并起来，就是分治策略的思想。本问题和其他分治问题不同的地方在于，不是简单地把大问题当成小规模问题的示例，合并的条件是必须跨越中点。

       下面给出上面问题求解的c源代码，关键的地方是一下几句代码：

        threeParmLeft=findMaxinumSubarray(number,low,mid);

        threeParmRight=findMaxinumSubarray(number,mid+1,high);

        threeParmCross=findMaxCrossingSubarray(number,low,mid,high);

#include 
#define LENGTH 16
//定义一个结构，记录了左右下表和总和，原因在于用于数据返还
typedef struct
   {
     int low;
     int high;
     int sum;
   }parm;

parm findMaxCrossingSubarray(int number[],int low,int mid,int high);
parm findMaxinumSubarray(int number[],int low,int high);

int main()
{
    int number[LENGTH] = {13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7};

    parm threeParm;
    threeParm=findMaxinumSubarray(number,0,LENGTH-1);
    printf("%d,%d,%d",threeParm.low,threeParm.high,threeParm.sum);
    return 0;

}
parm findMaxinumSubarray(int number[],int low,int high)
{
    int mid;
    parm threeParmLeft;
    parm threeParmRight;
    parm threeParmCross;
    parm threeParm;
//递归停止条件
    if (low==high)
    {
        threeParm.low=low;
        threeParm.high=high;
        threeParm.sum=number[low];
        return threeParm;
    }
    else
    {
        //分治策略        
        mid=(low+high)/2;

        threeParmLeft=findMaxinumSubarray(number,low,mid);
        threeParmRight=findMaxinumSubarray(number,mid+1,high);
        threeParmCross=findMaxCrossingSubarray(number,low,mid,high);
        //下标更新        
        if (threeParmLeft.sum>threeParmRight.sum&&threeParmLeft.sum>threeParmCross.sum)
            return threeParmLeft;
        else if (threeParmRight.sum>threeParmLeft.sum&&threeParmRight.sum>threeParmCross.sum)
              return threeParmRight;
        else
            return threeParmCross;
      }
}
parm findMaxCrossingSubarray(int number[],int low,int mid,int high)
{
    int i;
    parm threeParm;
    //左搜索
    int sum=0;
    int leftSum=number[mid]-1;
    int left;

    for (i=mid;i>=low;i--)
    {
        sum=sum+number[i];
        if(sum>leftSum)
        {
            leftSum=sum;
            left=i;
        }
    }
    //右搜索
    sum=0;
    int rightSum=number[mid+1]-1;
    int right;
    for (i=mid+1;i<=high;i++)
    {
        sum=sum+number[i];
        if(sum>rightSum)
        {
            rightSum=sum;
            right=i;
        }
    }
    threeParm.low=left;
    threeParm.high=right;
    threeParm.sum=leftSum+rightSum;
    return threeParm;
}