Educational Codeforces Round 92 (ABCDE)题解

昨晚打了上面的那一场教育场，觉得有趣，然后又模拟了一下上一场教育场，找找状态手感，顺便静一静心。

								A

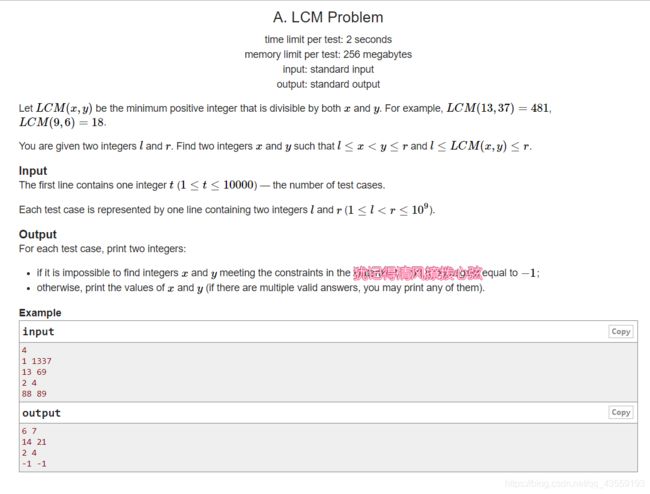
题意：
给你两个数: l , r 。问你是否存在两个数x,y( l <= x,y <= r && x != y ) 使得 l <= lcm（x,y）<= r。
思路：
判断 r 是否 >= l*2 ,如果是 ，输出( l , 2 * l ) 即可，否则 输出（-1 -1）。
简单证明：证明就不证明了，因为电脑写公式太麻烦了（自己还不会用），自己写写就可以发现 ，比如 l = 12 , r =20 想明白这个应该就会证明了吧。
。

								B

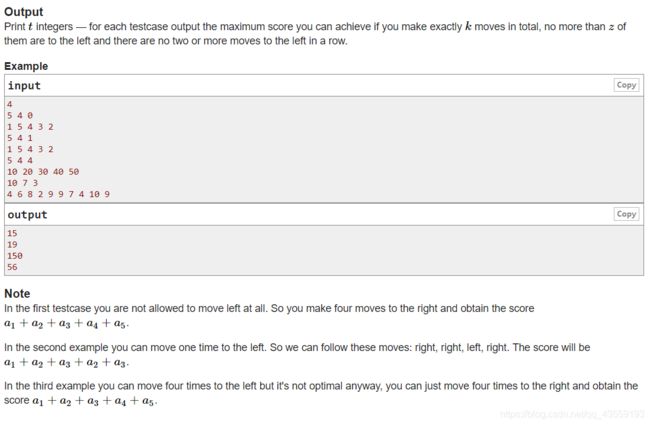
题意很有意思，小伙伴喊我去打lol我就不翻译啦，自己看看啦。
直接上思路：
我是枚举z，加分类讨论写的，具体实现看代码。

								C

题意读完题目就ok了。
思路：
分别考虑奇偶的情况。
自己手玩一下会发现一些好玩的性质。
会发现如果你要找的长度是奇数，那么那个串内只能有一种数。
如果是偶数的话，那么这个串内只能由两种数，而且必须是abababab这种形式。
对于奇数就很好处理，偶数也一样，枚举a是什么，b是什么分别考虑就行了。具体实现等下看代码。

								D

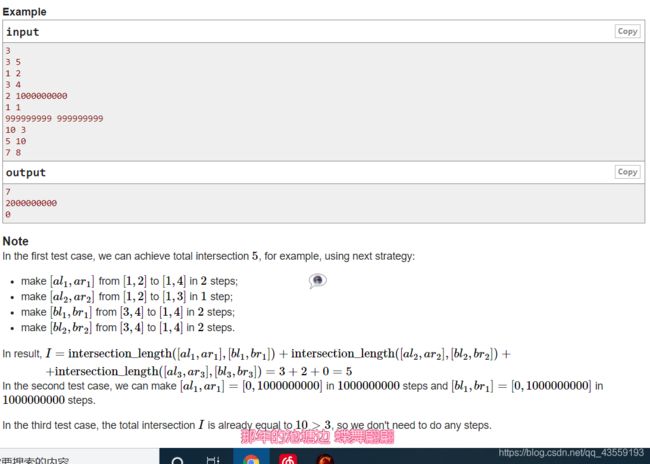
题意不是很好表达，读者仔细读读就好。
思路：
我是直接枚举我们需要用到几条线段，然后分类讨论的，具体实现看代码。

								E

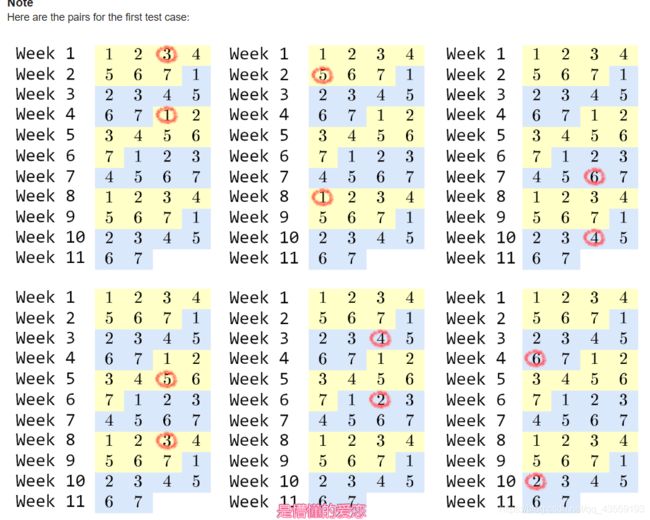
题意就是问你有多少组(x,y)满足那个条件。
式子化简化简会得到：（x-y）(d-1) = 0 % w.
如果（d-1）是w的倍数，很好写。
然后不是的话，把(d-1)和w求gcd，然后约掉gcd。w’ = w / gcd ;
然后找到(x-y) 是 w’ 的倍数的组的数量即可。
x-y = w’ 的组数是min(m,d)- w’ 。
枚举w’ ,w’*2 ,w’3…
然后会发现用等差数列求和公式能O1求出来。
具体实现看代码.

							A

#include
using namespace std;
const int N=1e3+15;
typedef long long ll;
int main()
{
    ll t;
    cin>>t;
    while(t--)
    {
        ll l,r,x,y;
        cin>>l>>r;
        if(r<l*2)
        {
            cout<<"-1 -1"<<endl;
        }
        else
        {
            cout<<l<<" "<<(l*2)<<endl;
        }
    }
    return 0;
}

							B

#include
using namespace std;
const int N=1e6+15;
typedef long long ll;
ll sum1[N],sum2[N],a[N];
int main()
{
    ll t,n,k,z;
    cin>>t;
    while(t--)
    {
        cin>>n>>k>>z;
        for(int i=1;i<=n;i++)
        {
            cin>>a[i];
            /*sum1[i]=sum1[i-1]+a[i];
            sum2[i]=max(sum2[i-1],a[i]+a[i+1]);
            */
        }
        for(int i=1;i<=n;i++)
        {
            sum1[i]=sum1[i-1]+a[i];
            sum2[i]=max(sum2[i-1],a[i]+a[i+1]);
        }
        ll op=sum1[k+1];
        //cout<
        if(z*2>k)
        {
            z=k/2;
        }
        for(int i=1;i<=z;i++)
        {
            //if()
            op=max(op,sum1[k+1-2*i]+i*sum2[k+1-2*i]);
        }
        cout<<op<<endl;
    }
    return 0;
}

								C

#include
using namespace std;
const int N=5e5+15;
typedef long long ll;
char str[N];
ll a[N],dp[12][N];
int main()
{
    ll t;
    cin>>t;
    while(t--)
    {
        scanf("%s",str+1);
        int n=strlen(str+1);
        for(int i=1;i<=n;i++)
        {
            a[i]=int(str[i]-'0');
            for(int j=0;j<=9;j++)
            {
                dp[j][i]=dp[j][i-1];
            }
            dp[a[i]][i]++;
        }
        ll maxn=0;
        for(int i=0;i<=9;i++)
        {
            maxn=max(maxn,dp[i][n]);
        }
        for(int x=0;x<=9;x++)
        {
            for(int y=0;y<=9;y++)
            {
                if(x==y)    continue;
                ll op=0;
                for(int i=1;i<=n;i++)
                {
                    if(a[i]==x)
                    {
                        if(op%2==0)
                            op++;
                    }
                    if(a[i]==y)
                    {
                        if(op%2==1)
                            op++;
                    }
                }
                if(op%2==1) op--;
                maxn=max(maxn,op);
            }
        }
        cout<<(n-maxn)<<endl;
    }
    return 0;
}

							D

#include
using namespace std;
const int N=1e3+15;
typedef long long ll;
int main()
{
    ll t,n,k,l1,l2,r1,r2;
    cin>>t;
    while(t--)
    {
        cin>>n>>k;
        cin>>l1>>r1;
        cin>>l2>>r2;
        if(r1>r2)
        {
            swap(l1,l2);    swap(r1,r2);
        }
        ll maxn=1123456789123456;
        if(r1<=l2)
        {
            ll d=l2-r1;

            ll spend = r2-r1 + l2-l1 ;
            ll cost  = r2-l1;
            for(int i=1;i<=n;i++)
            {
                if( (i-1) * cost >= k )   break;
                ll op = k - (i-1) * cost , od = (i-1)*spend ;
                if(op >=cost )
                {
                    ll ow = op - cost;  od += spend;
                    od+=(ow*2);
                    maxn=min(maxn,od);
                }
                else
                {
                    od += d ;   od += ( op ) ;
                    maxn=min(maxn,od);
                }
            }
        }
        else
        {
            if(l2<=l1)
            {
                ll cost = r1 - l1 ;
                if( n * cost >= k  )
                {
                    maxn=0;
                }
                else
                {
                    ll op= k - n*cost;
                    ll ex = l1 - l2 +  r2 - r1 ;
                    if( n*ex >=op )
                    {
                        maxn = op ;
                    }
                    else
                    {
                        maxn = n*ex;
                        ll od = op - n*ex;
                        maxn+=od*2;
                    }
                }
            }
            else
            {
                ll cost = r1 - l2 ;
                if(n*cost>=k)
                {
                    maxn=0;
                }
                else
                {
                    ll op = k - n*cost;
                    ll ex = (r2-r1) + (l2-l1) ;
                    if( n * ex >= op )
                    {
                        maxn = op;
                    }
                    else
                    {
                        maxn = n * ex ;
                        ll od = op - ex*n ;
                        maxn += od *2;
                    }
                }
            }
        }
        cout<<maxn<<endl;
    }
    return 0;
}
/*
3
3 5
1 2
3 4
2 1000000000
1 1
999999999 999999999
10 3
5 10
7 8
*/

								E

#include
using namespace std;
const int N=1e3+15;
typedef long long ll;
ll gcd(ll a,ll b)
{
    if(b==0)
        return a;
    return gcd(b,a%b);
}
int main()
{
    ll t,m,d,w,ans;
    cin>>t;
    while(t--)
    {
        cin>>m>>d>>w;
        if(d%w==1)      ///d会小于w吗？ 后来发现小不小无所谓，就不用再分类了。
        {
            m=min(m,d);
            ans=m*(m-1)/2;
            cout<<ans<<endl;
        }
        else
        {
            ll op=gcd(d-1,w),ok;
            w/=op;  ll md=min(m,d);
            ll n=md/w;    op=n;
            op=op*(op+1)/2; op=op*w;
            op=md*n-op;
            cout<<op<<endl;
        }
    }
    return 0;
}