数值计算方法--线性方程组的数值解法(3) 追赶法(Thomas)，选择主元(Pivoting)，求逆(Inversion)

追赶法
追赶法适用于三对角矩阵，形如$$\left(\begin{array}{ccccc}X& X& 0& 0& 0\\ X& X& X& 0& 0\\ 0& X& X& X& 0\\ 0& 0& X& X& X\\ 0& 0& 0& X& X\end{array}\right)$$对于100×100矩阵，使用的空间约为原先的33：1。对这种矩阵做杜丽特分解(或克洛特分解)。假设中间第K行存储着c_k,d_k,e_k三个元素，类似$$\left(\begin{array}{cccccc}...& ...& ...& ...& ...& ...\\ ...& c_{k-1}& d_{k-1}& e_{k-1}& 0& ...\\ ...& 0& c_k& d_k& e_k& ...\\ ...& & & & & ...\end{array}\right)$$执行操作$$rowk\leftarrow rowk-(c_{k-1}/d_{k-1})\times row(k-1)$$执行杜丽特分解时，发现该行的e并未受到影响。把算子λ=c_k-1/d_k-1存储在以前c_k-1的位置。所以得到如下程序片段(暂不能运行)。

for k = 2:n
    lambda = c(k-1)/d(k-1);
    d(k) = d(k) - lambda*e(k-1);
    c(k-1) = lambda;
end

以此类推，可以想象得到L矩阵对角线元素对应的下一行从左上到右下分别是c₁，c₂…c_n-1。用这个单位下三角矩阵解出中间向量y。由于每次只需减掉一项，代码较前述LU分解简单。

y(1) = b(1)
for k = 2:n
	y(k) = b(k) - c(k-1)*y(k-1);
end

顺理成章，使用回代法根据y、U解出x。U中的e_n没有改变，而d_n由于消去过程与原矩阵不同。

x(n) = y(n)/d(n);
for k = n-1:-1:1
	x(k) = (y(k) - e(k)*x(k+1))/d(k);
end

matlab函数实现如下(可运行)：

function [c,d,e] = ThomasDec(c,d,e)
% calculating LU decomposition of tridiagonal matrix A = [c\d\e].
n = length(d);
for k = 2:n
	lambda = c(k-1)/d(k-1);
	d(k) = d(k) - lambda*e(k-1);
	c(k-1) = lambda;
end

function x = ThomasSol(c,d,e,b)
% Solves A*x = b where A = [c\d\e] is the LU
n = length(d);
for k = 2:n % Forward substitution
	b(k) = b(k) - c(k-1)*b(k-1);
end
b(n) = b(n)/d(n); % Back substitution
for k = n-1:-1:1
	b(k) = (b(k) -e(k)*b(k+1))/d(k);
end
x = b;

例如，解书(《数值计算方法》，马东升等著，机械工业出版社)P85例题：

在命令行中输入

c = [-1 -2 -3];
d = [2 3 4 5];
e = [-1 -2 -2];
b=[3 1 0 -5];
[c,d,e]=ThomasDec(c,d,e);
x = ThomasSol(c,d,e,b)

得到结果一致。

同理，此类形状的对称矩阵都可以用追赶法得出数值解。这里有一个[f\e\d\e\f]型的系数矩阵构成的线性方程$$\left(\begin{array}{cccccc}6& -4& 1& 0& 0& ...\\ -4& 6& -4& 1& 0& ...\\ 1& -4& 6& -4& 1& ...\\ & & ...& & & \\ & & ....& & & \\ & & ....& & & \\ & & ...& & & \\ & & ...& & & \\ ...& 0& 1& -4& 6& -4\\ ...& 0& 0& 1& -4& 7\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\\ x_7\\ x_8\\ x_9\\ x_{10}\end{array}\right)=\left(\begin{array}{c}3\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 4\end{array}\right)$$
复杂处在杜丽特分解的每一步需要同时对两行进行操作，但总体原理是一样的。代码如下：

function [d,e,f] = ThomasDec5(d,e,f)
% LU decomposition of pentadiagonal matrix A = [f\e\d\e\f].
n = length(d);
for k = 1:n-2
	lambda = e(k)/d(k);
	d(k+1) = d(k+1) - lambda*e(k);
	e(k+1) = e(k+1) - lambda*f(k);
	e(k) = lambda;
	lambda = f(k)/d(k);
	d(k+2) = d(k+2) - lambda*f(k);
	f(k) = lambda;
end
lambda = e(n-1)/d(n-1);
d(n) = d(n) - lambda*e(n-1);
e(n-1) = lambda;

function x = ThomasSol5(d,e,f,b)
% Solves A*x = b where A = [f\e\d\e\f] is the LU
% decomposition of the original pentadiagonal(五对角矩阵) A.
n = length(d);
b(2) = b(2) - e(1)*b(1); % Forward substitution
for k = 3:n
    b(k) = b(k) - e(k-1)*b(k-1) - f(k-2)*b(k-2);
end
b(n) = b(n)/d(n); % Back substitution
b(n-1) = b(n-1)/d(n-1) - e(n-1)*b(n);
for k = n-2:-1:1
    b(k) = b(k)/d(k) - e(k)*b(k+1) - f(k)*b(k+2);
end
x = b;

在命令行中打下

n = 10;
d = 6*ones(n,1); d(n) = 7;
e = -4*ones(n-1,1);
f = ones(n-2,1);
b = zeros(n,1); b(1) = 3; b(n) = 4;
[d,e,f] = ThomasDec5(d,e,f);
x = ThomasSol5(d,e,f,b)

得

变换主元
按顺序消元可能出现主元素a_kk^(k)=0，尽管系数矩阵非奇异消元也无法进行。例如，形如方程组$$10^{-5}{x}_1+x_2=1$$$$x_1+x_2=2$$如果不改变方程组次序，用四位浮点数的计算机高斯消去法求解，得到$$\left(\begin{array}{cc}10^{-5}& 1\\ 0& 1-10^5\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{c}1\\ 2-10^5\end{array}\right)$$由于只能精确4位（a₁₁计算机未处理所以保留原样）$$\left(\begin{array}{cc}10^{-5}& 1\\ 0& -10^5\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{c}1\\ -10^5\end{array}\right)$$这样得到x₂=1 x₁=0,严重失真。而将上下两式颠倒重复以上动作，却能得到正确结果。可以发现，当$$|A_{ii}|>\sum _{j=1,j\ne i}^n|A_{ij}|(i=1,2,...,n)$$即对角占优时，颠倒操作不会再带来更优化的结果。这是列主元（行交换）高斯消去(也可用在LU分解)中使用的原则。
列主元高斯消去法

创立一个表示某行最大元素的数组s$$s_i=ma{x}_j|A_{ij}|,i=1,2,...,n$$两行代码算得：

for i in range(n):
	s[i] = max(abs(a[i,0:n]))

在高斯消元的每一步(比方第k步)，在第k列寻找$$r_{pk}=ma{x}_{j\ge k}{r}_{jk}$$若不是第k行，则将k行和p行替换。每一步换行要连带标定数组s一起变换。换行代码如下：

function v = GaussSwapRows(v,i,j)
% Swap rows i and j of vector or matrix v.
temp = v(i,:);
v(i,:) = v(j,:);
v(j,:) = temp;

function x = gaussSwapPiv(A,b)
% Solves A*x = b by Gauss elimination with row pivoting.
if size(b,2) > 1; b = b'; end
n = length(b); s = zeros(n,1);
%----------设置标定数组----------
for i = 1:n
    s(i) = max(abs(A(i,1:n))); 
end
%---------按 需 换 行----------
for k = 1:n-1
    
    [Amax,p] = max(abs(A(k:n,k))./s(k:n));
    p = p + k - 1;
    if Amax < eps
        error('Matrix is singular');
    end
    if p ~= k
        b = GaussSwapRows(b,k,p);
        s = GaussSwapRows(s,k,p);
        A = GaussSwapRows(A,k,p);
    end
%--------------消 去 过 程---------------
    for i = k+1:n
        if A(i,k) ~= 0
            lambda = A(i,k)/A(k,k);
            A(i,k+1:n) = A(i,k+1:n) - lambda*A(k,k+1:n);
            b(i) = b(i) - lambda*b(k);
        end
    end
end
%------------回 代 过 程----------
for k = n:-1:1
b(k) = (b(k) - A(k,k+1:n)*b(k+1:n))/A(k,k);
end
x = b;

同理，解书上一道例题

在命令行中输入

 A = [0.5 1.1 3.1;
2.0 4.5 0.36;
5.0 0.96 6.5];
>> b=[6 0.02 0.96];
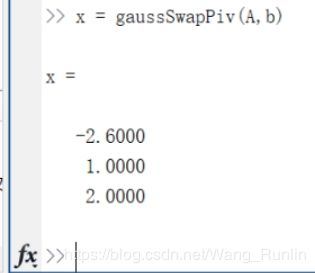
>> x = gaussSwapPiv(A,b)

结果与答案一致。

列主元LU分解
如前所述，高斯消元法可以将每一步变换当作一个初等矩阵左乘，将这些初等矩阵乘在一起得到单位下三角矩阵L，即杜丽特分解。类似地，也可以在LU分解中使用列主元方法。增加的要求是每次换行时都要有记录，以便调整常数向量的顺序。在程序中创建排列数组perm（permutation），初始值[1,2,…,n]^T。每当换行，perm里数的顺序相应改变。这个数组后续传入求解函数中，将常数向量调整到同一顺序，再顺代和回代求出解。

function [A,perm] = LUdecPiv(A)
% LU decomposition of matrix A; returns A = [L\U] and ’perm’.
n = size(A,1); s = zeros(n,1);
perm = (1:n)';
%----------设 置 标 定 数 组----------
for i = 1:n; s(i) = max(abs(A(i,1:n))); end
%---------按 需 换 行----------
for k = 1:n-1
    [Amax,p] = max(abs(A(k:n,k))./s(k:n));
    p = p + k - 1;
    if Amax < eps
    error('Matrix is singular')
    end
    if p ~= k
        s = gaussSwapRows(s,k,p);
        A = gaussSwapRows(A,k,p);
    	perm = gaussSwapRows(perm,k,p);
    end
%--------------消 去 过 程---------------
    for i = k+1:n
        if A(i,k) ~= 0
            lambda = A(i,k)/A(k,k);
            A(i,k+1:n) = A(i,k+1:n) - lambda*A(k,k+1:n);
            A(i,k) = lambda;
        end
    end
end

命令行中输入

A = [2 -1 1;
4 2 1
2 1 2];b=[5;4;5];
[A,perm]=LUdecPiv(A);
x = LUsolPiv(A,b,perm)

结果与答案一致。

求逆矩阵
使用以上众算法，可以用比伴随矩阵法更高效地求逆阵，也即对每个列向量跟随着做初等行变换。程序中直接嵌套上述已完善的LUsolPiv、LUdecPiv来实现。

function Ainv = matInv(A)
% Inverts martix A with LU decomposition.
n = size(A,1);
Ainv = eye(n); % Store RHS（right hand side） vectors in Ainv.
[A,perm] = LUdecPiv(A); % 分解 A.
% 逐一解右边的向量将结果存储在Ainv中
% replacing the corresponding RHS vector.
for i = 1:n
    Ainv(:,i) = LUsolPiv(A,Ainv(:,i),perm);
end

在命令行中输入

A = [0.6 -0.4 1.0
-0.3 0.2 0.5
0.6 -1.0 0.5];
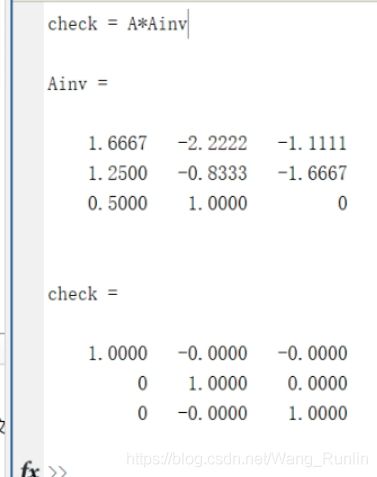
Ainv = matInv(A)
check = A*Ainv

结果表明求解正确。