Large Scale Evolving Graphs with Burst Detection

Large Scale Evolving Graphs with Burst Detection

Abstract

Analyzing large-scale evolving graphs are crucial
for understanding the dynamic and evolutionary nature of social networks. Most existing works focus on discovering repeated and consistent temporal patterns, however, such patterns cannot fully explain the complexity observed in dynamic networks. For example, in recommendation scenarios, users sometimes purchase products on a whim during a window shopping. Thus, in this paper, we design and implement a novel framework called BurstGraph which can capture both recurrent and consistent patterns, and especially unexpected bursty network changes. The performance of the proposed algorithm is demonstrated on both a simulated dataset and a world-leading E-Commerce company dataset,
showing that they are able to discriminate recurrent
events from extremely bursty events in terms of action propensity.
分析大规模演化图至关重要了解社交网络的动态和进化性质。 现有的大多数工作都集中在发现重复和一致的时间模式上，但是，这种模式不能完全解释动态网络中观察到的复杂性。 例如，在推荐方案中，用户有时会在橱窗购物期间一时兴起地购买产品。 因此，在本文中，我们设计并实现了一个名为BurstGraph的新颖框架，该框架既可以捕获循环模式又可以捕获一致的模式，尤其是突发网络突发变化。 在模拟数据集和世界领先的电子商务公司数据集上均展示了所提出算法的性能， 表明他们能够区分复发 就行动倾向而言，这些事件是由突发事件引起的。

1 Introduction

Dynamic networks, where edges and vertices arrive over time, are ubiquitous in various scenarios, (e.g., social media, security, public health, computational biology and user-item purchase behaviors in the E-Commerce platform [Akoglu and Faloutsos, 2013; Akoglu et al., 2015]), and have attracted significant research interests in recent years. An important problem over dynamic networks is burst detection – finding objects and relationships that are unlike the normal. There are many practical applications spanning numerous domains of burst detection, such as bursty interests of users in E-Commerce [Parikh and Sundaresan, 2008], cross-community relationships in social networks. Recently, the research community has focused on network embedding learning. One class of the network embedding methods represent nodes as single points in a low-dimensional latent space, which aims to preserve structural and content information of the network [Perozzi et al., 2014; Grover and Leskovec, 2016]. Other classes include edge embedding and subgraph embedding [Dong et al., 2017]. However, most existing network embedding methods mainly focus on the network structure, ignoring the bursty links appearing in the dynamic networks [Perozzi et al., 2014; Dai et al., 2016; Qiu et al., 2018].
随着时间的流逝，边缘和顶点随时间到达的动态网络无处不在（例如，社交媒体，安全性，公共卫生，计算生物学和电子商务平台中的用户项购买行为[Akoglu和Faloutsos，2013； Akoglu等人，2015]），并且近年来引起了重要的研究兴趣。动态网络上的一个重要问题是突发检测-查找与正常对象不同的对象和关系。有许多跨突发检测领域的实际应用，例如电子商务中用户的突发兴趣[Parikh and Sundaresan，2008]，社交网络中的跨社区关系。最近，研究社区已将重点放在网络嵌入学习上。一类网络嵌入方法将节点表示为低维潜在空间中的单个点，旨在保留网络的结构和内容信息[Perozzi等人，2014； Grover和Leskovec，2016年]。其他类别包括边缘嵌入和子图嵌入[Dong等，2017]。但是，大多数现有的网络嵌入方法主要关注网络结构，而忽略了动态网络中出现的突发链接[Perozzi等人，2014年； Dai等，2016; Qiu et al。，2018]。
In social network dynamics, users may generate consistent temporal patterns by buying consumable goods, such as food and papers, to satisfy their recurrent needs; or purchasing durable products, such as cell phones and cars, to satisfy their longtime needs. However, in the real world, bursty links are very common in network evolution. For instance, in a social network, people will meet new friends or discover new interests if they are in a new environment; in an E-Commerce
network, customers often do window shopping when they are exploring recommendation sections. Figure 1 illustrates the interest evolution of the young lady during shopping. However, existing works on modeling dynamic networks mostly focus on repeated and consistent patterns [Trivedi et al., 2017; Li et al., 2017; Zhou et al., 2018], and cannot well capture bursty links due to their sparsity. Such important bursty information is commonly viewed as noisy data in the general machine learning algorithms and ignored in modeling [Chandola et al.,2009]. Furthermore, these bursty dynamics are hidden in other complex network dynamics, including the addition/removal of edges and the update of edge weights. It is challenging to design a framework to account for all these changes.

在社交网络动态中，用户可以通过购买诸如食品和纸张之类的消费品来生成一致的时间模式，以满足其经常性需求；或购买耐用产品，例如手机和汽车，以满足其长期需求。但是，在现实世界中，突发链接在网络演进中非常普遍。例如，在社交网络中，人们在新环境中会结识新朋友或发现新兴趣；在电子商务中, 通过网络，客户在浏览推荐部分时经常会逛逛。图1说明了购物过程中年轻女士的兴趣演变。然而，现有的对动态网络建模的工作主要集中在重复和一致的模式上[Trivedi et al。，2017; Li等人，2017; Zhou et al。，2018]，由于稀疏性无法很好地捕获突发链接。这些重要的突发信息在一般的机器学习算法中通常被视为嘈杂的数据，而在建模中则被忽略[Chandola等，2009]。此外，这些突发动态隐藏在其他复杂的网络动态中，包括边的添加/删除和边权重的更新。设计一个框架以应对所有这些变化是具有挑战性的。

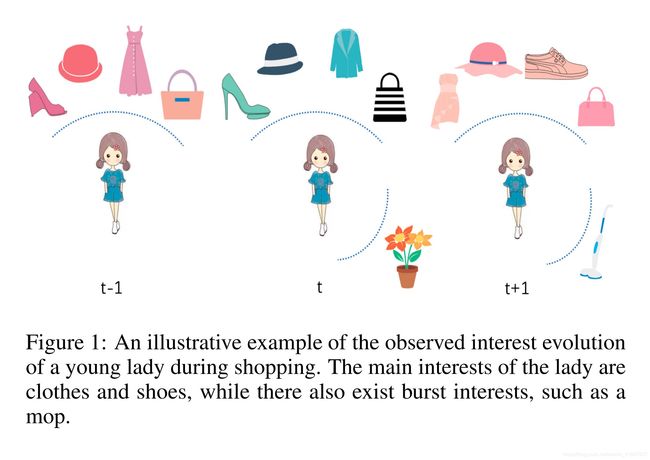
Figure 1: An illustrative example of the observed interest evolution of a young lady during shopping. The main interests of the lady are clothes and shoes, while there also exist burst interests, such as a mop.
To tackle the aforementioned challenges, we propose a
novel framework with contributions summarized as follows:

图1：购物期间观察到的年轻女士的兴趣演变的示例。 这位女士的主要兴趣是衣服和鞋子，同时还存在一些突发性兴趣，例如拖把。为了应对上述挑战，我们建议新颖的框架，其贡献总结如下：

• Problem Formulation:

we formally define the problem of evolving graphs with bursty links. The key idea is to detect bursty links in dynamic graphs during their onset.
我们正式定义了带有突发链接的演化图的问题。 关键思想是检测动态图中的突发链接。

• Algorithms:

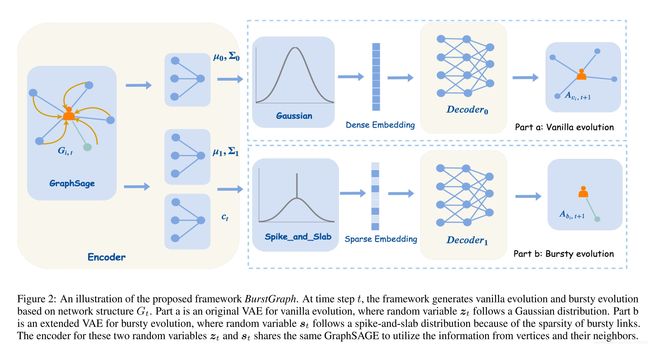
we propose a novel framework for modeling evolving graphs with bursty links, namely BurstGraph. BurstGraph divides graph evolution into two parts: vanilla evolution and bursty links’ occurrences. For the sparsity of bursty links, a spike-and-slab distribution [Mitchell and Beauchamp, 1988] is introduced as an approximation posterior distribution in the variational autoencoder (VAE)[Kingma and Welling, 2013] framework, while vanilla evolution accepts the original framework of VAE. To fully exploit the dynamic information in graph evolution, we propose an RNN-based dynamic neural network by capturing graph structures at each time step.
The cell of RNN maintains information of both vanilla
and bursty evolution, which is updated over time.
The rest of this paper is organized as follows: Section 2
briefly reviews related work. Section 3 introduces the problem statement of evolving graphs with bursty links and presents the proposed framework. Experiments on both simulated dataset and real datasets are presented in Section 4 with discussions. Finally, Section 5 concludes the paper and visions the future work.

2 Related Work

Static Network Embedding. Recently, learning representations for networks has attracted considerable research efforts. Inspired by Word2Vec [Mikolov et al., 2013], [Perozzi et al., 2014; Grover and Leskovec, 2016] learn a node representation with its neighborhood contexts. As an adjacency matrix is used to represent the topology of a network, representative works, such as [Qiu et al., 2018], use matrix factorization to learn low-rank space for the adjacency matrix. Deep learning methods [Wang et al., 2016] are proposed to introduce effective non-linear function learning in network embedding. Dynamic Network Embedding. Actually, inductive static methods [Perozzi et al., 2014; Hamilton et al., 2017a] can also handle dynamic networks by making inference of the new vertices. [Du et al., 2018] extends the skip-gram methods to update the original vertices’ embedding. [Zhou et al., 2018] focuses on capturing the triadic structure properties for learning network embedding. Considering both the network structure and node attributes, [Li et al., 2017] focuses on updating the top eigenvectors and eigenvalues for the streaming network.
Burst Detection. Traditionally, burst detection is to detect
an unexpectedly large number of events occurring within some time duration. There are two typical types of burst detection approaches, i.e., threshold-based [Heard et al., 2010] and statebased methods [Kleinberg, 2003]. [Heard et al., 2010] studies fast algorithms using self-similarity to model bursty time series. [Kleinberg, 2003] uses infinite-state automaton to model the burstiness and extract structure from text streams. However, the link building of evolving graphs is usually sparse and slow, where unexpected links are rare to occur simultaneously. Therefore, our definition of a burst is simply an unexpected behavior within a time duration, which is a straightforward definition adopted by many applications in the real world.

3 The Proposed Model

Existing dynamic network embedding methods mainly focus on the expansion of new vertices and new edges, but usually ignore the changes of vertices’ attributes through time that lead to unexpected bursty network changes [Angel et al., 2012].

3.1 VAE for Graph Evolution

Training.

We adopt Adam optimizer [Kingma and Ba,
2014] to optimize the objective and also introduce dropout
with weight penalties into our proposed model. As expected, we penalize L1-norm of weight Ws to induce the sparsity of the output. It is worth to note that all the parameters of our proposed model are shared along dynamic graphs over time interval (1, T). GraphSAGE in encoder network also shares a random features input for each vertice over time interval (1, T). The edge evolution is always sparse and unbalanced, which brings trouble to identify the positive instances to achieve better performance. Instead of traditional sigmoid cross entropy loss function, we use inter-and-intra class balanced loss in our model:

4 Experiment

In this section, we evaluate our model in the dynamic setting from the performance on the multi-class link prediction. Dataset. We first use the simulated data to verify the effectiveness of the model, then we apply BurstGraph to a real challenging dataset from a world-leading E-Commerce company.

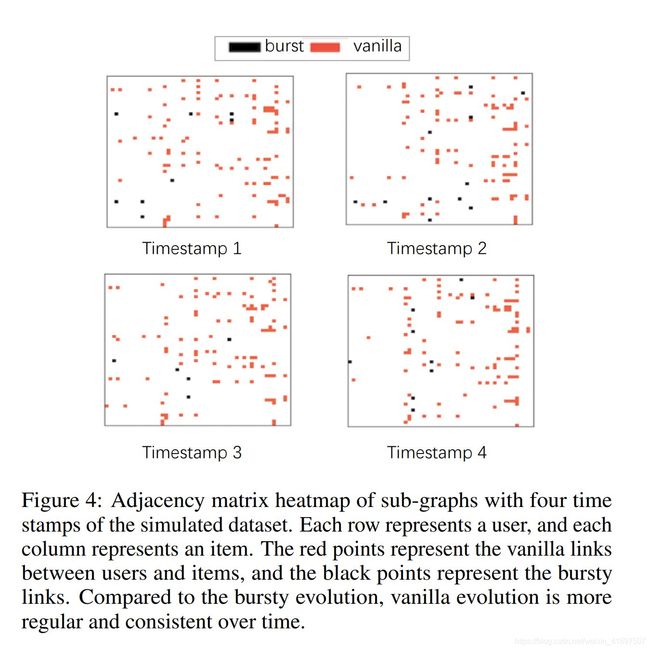
• Simulated Dataset: We generate a sequence of synthetic bipartite graph snapshots of 21K vertices and 527K edges that share similar characteristics as real data. We assume that each vertex has two types (vanilla/burst) of representations. More specifically, we divide the generation process into two parts: the first part is to generate hyperparameters for each vertex to ensure the independence; the second part is to generate links by sampling two representations of vertices from Gaussian distributions

• Alibaba Dataset: We collect this dataset from a worldleading E-Commerce company Alibaba with two types of nodes, user and item. The bursty link between user and item is defined as if the user has no interaction with the item or similar items in the same category during the last 15 days according to business needs. The other links are viewed as vanilla links. With dynamic graph setting, we split the whole graph into a sequence of graph snapshots with the same time interval (e.g., 1 day). The dataset with sampled items is denoted as Alibaba-S dataset. The statistics of the above datasets are shown in Table 2. In each dataset, graph snapshot Gt consists of all the nodes and interactions that appear at time step t. In our experimental setting, we hide a set of edges from the original graph and train on the remaining graph. The test dataset contains 10% randomly selected vertices, while the negative links are also randomly selected with the same number of positive links for each link type (vanilla/burst). Baseline Methods We compare our model against the following network embedding algorithms.

Figure 4: Adjacency matrix heatmap of sub-graphs with four time stamps of the simulated dataset. Each row represents a user, and each column represents an item. The red points represent the vanilla links between users and items, and the black points represent the bursty links. Compared to the bursty evolution, vanilla evolution is more regular and consistent over time.
• DeepWalk: DeepWalk1
[Perozzi et al., 2014] is a representative embedding method for static network. DeepWalk generates truncated random walks and uses Skipgram algorithm [Mikolov et al., 2013] to learn latent representations by treating walks as the equivalent of sentences.
• GraphSAGE: GraphSAGE2
[Hamilton et al., 2017b] is a general inductive framework of network embedding, which leverages topological structure and attribute information of vertices to efficiently generate vertex embedding. Besides, GraphSAGE can still maintain a good performance even with random features input.
• CTDNE: CTDNE [Nguyen et al., 2018] is a continuoustime dynamic network embedding method. CTDNE generates temporal random walk as the context information of each vertex and uses Skip-gram algorithm to learn latent representations. In this method, the time of each edge is simply valued according to the number of its
snapshot.

• TNE: TNE3
[Zhu et al., 2016] is a dynamic network embedding algorithm based on matrix factorization. Besides,
this method holds a temporal smoothness assumption
to ensure the continuity of the embeddings in evolving
graphs.
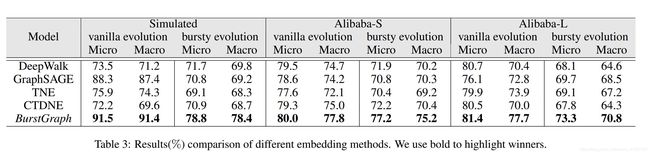
It is worthy to mention, DeepWalk and GraphSAGE are static network embedding methods. To facilitate the comparison between our method and these relevant baselines, these two methods are trained with the whole graph, which includes all graph snapshots. In the following, we compare the performance of these methods with BurstGraph4 on three datasets in terms of Micro-F1 and Macro-F1. Comparison Results. Table 3 shows the overall performance of different methods on three datasets. Our model BurstGraph is able to consistently outperform all sorts of baselines in various datasets. Next we compare and analyze results on vanilla evolution and burst links, respectively. For the vanilla evolution, BurstGraph has a performance gain of
+1.4% in terms of Micro-F1 and +3.5% in terms of Macro-F1 on average. For the bursty evolution, BurstGraph outperforms other methods +5.5% in terms of Micro-F1 and +5.3% in terms of Macro-F1 averagely. These results show that splitting evolving graphs into vanilla and bursty evolution not only benefits for the performance of the bursty evolution, but also benefits for that of the vanilla evolution. Moreover, compared to other baselines, the performance of BurstGraph is quite robust over the three datasets. Notice that DeepWalk, CTDNE and TNE perform poorly on the simulated dataset. One potential reason could be that the simulated generation process may be easier for message passing algorithms (e.g., GraphSAGE) compared to matrix factorization based methods (e.g., DeepWalk, CTDNE or TNE). Parameter Analysis. We investigate the sensitivity of different hyperparameters in BurstGraph including importance
weight λ and random variable dimension d. Figure 5 shows the performance of BurstGraph on Alibaba-S dataset when altering the importance weight λ and variable dimension d, respectively. From part a), we can see that the performance of vanilla link prediction is stable when changing the importance
weight λ. The performance of burst link prediction rises with the increase of importance weight λ and converges slowly when importance weight is larger than 1. From part b), we can conclude that the performance of BurstGraph is relatively stable within a large range of variable dimension, and the performance decreases when the variable dimension is either too small or too large.
Visualization of vertex representations. We visualize the
embedding vectors of sampled vertices in the simulated dataset and Alibaba-S dataset learned by BurstGraph. We project the embedding vectors to a 2-dimensional space with t-SNE method. As shown in Figure 6, embeddings from the vanilla evolution can be clearly separated from embeddings of the bursty evolution. More specifically, the embeddings of vertexes in the vanilla evolution evenly spread out in the space, while the embeddings of vertexes in the bursty evolution gather in a relatively small area. The reason could be that the vertex embedding in the vanilla evolution is highly depended on its attributes, while the vertex embedding in the bursty evolution is another way around because of sparsity.

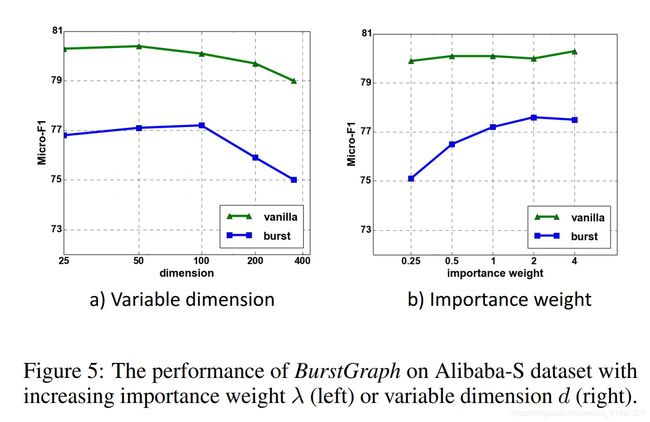
Figure 6: 2D visualization on embeddings (100 randomly selected vertices) for vanilla evolution and bursty evolution. This visualizes the embeddings from vanilla and bursty evolution on Simulated dataset (left) and Alibaba-S dataset (right). Embeddings from vanilla evolution are spread out while embeddings from bursty evolution concentrate in a relatively small area.

5 Conclusion

In this work, we propose a novel approach for evolving graphs and assume that the evolving of edges in a sequence of graph snapshots can be split into two parts: vanilla and bursty evolution. In addition, these two parts utilize variational autoencoders based on two different prior distributions to reconstruct the graph evolution, respectively. The vanilla evolution follows a Gaussian distribution, when the burst evolution follows a spike-and-slab distribution. Experiment results on real-world datasets show the benefits of our model on bursty links prediction in evolving graphs. However, there still exist limitations in our model. First, only bursty links are considered in our framework. However, there exist other bursty objects, e.g., vertices and communities, which should also be taken into account. We plan to extend our approach to support these bursty objects in the future. Second, we plan to propose a new time series model that supports continuous inputs rather than discretized graph snapshots.

References

[Akoglu and Faloutsos, 2013] Leman Akoglu and Christos
Faloutsos. Anomaly, event, and fraud detection in large
network datasets. In WSDM, pages 773–774. ACM, 2013.
[Akoglu et al., 2015] Leman Akoglu, Hanghang Tong, and
Danai Koutra. Graph based anomaly detection and description: a survey. In Data Mining and Knowledge Discovery
29, volume 3, pages 626–688. ACM, 2015.
[Angel et al., 2012] Albert Angel, Nikos Sarkas, Nick
Koudas, and Divesh Srivastava. Dense subgraph maintenance under streaming edge weight updates for real-time
story identification. Proc. VLDB Endow., 5(6):574–585,
2012.
[Chandola et al., 2009] Varun Chandola, Arindam Banerjee,
and Vipin Kumar. Anomaly detection: A survey. ACM
Comput. Surv., 41(3):15:1–15:58, July 2009.
[Dai et al., 2016] Hanjun Dai, Bo Dai, and Le Song. Discriminative embeddings of latent variable models for structured
data. In International conference on machine learning,
pages 2702–2711, 2016.
[Dong et al., 2017] Yuxiao Dong, Nitesh V Chawla, and
Ananthram Swami. metapath2vec: Scalable representation
learning for heterogeneous networks. In Proceedings of the
23rd ACM SIGKDD international conference on knowledge
discovery and data mining, pages 135–144. ACM, 2017.
[Du et al., 2018] Lun Du, Yun Wang, Guojie Song, Zhicong
Lu, and Junshan Wang. Dynamic network embedding: An
extended approach for skip-gram based network embedding. In IJCAI, pages 2086–2092, 2018.
[Grover and Leskovec, 2016] Aditya Grover and Jure
Leskovec. node2vec: Scalable feature learning for
networks. In Proceedings of the 22nd ACM SIGKDD
international conference on Knowledge discovery and data
mining, pages 855–864. ACM, 2016.
[Hamilton et al., 2017a] Will Hamilton, Zhitao Ying, and
Jure Leskovec. Inductive representation learning on large
graphs. In Advances in Neural Information Processing
Systems, pages 1024–1034, 2017.
[Hamilton et al., 2017b] William L. Hamilton, Rex Ying, and
Jure Leskovec. Inductive representation learning on large
graphs. In NIPS, 2017.
[Heard et al., 2010] Nicholas A Heard, David J Weston, Kiriaki Platanioti, David J Hand, et al. Bayesian anomaly detection methods for social networks. The Annals of Applied
Statistics, 4(2):645–662, 2010.
[Ishwaran et al., 2005] Hemant Ishwaran, J Sunil Rao, et al.
Spike and slab variable selection: frequentist and bayesian
strategies. The Annals of Statistics, 33(2):730–773, 2005.
[Kingma and Ba, 2014] Diederik P Kingma and Jimmy Ba.
Adam: A method for stochastic optimization. arXiv
preprint arXiv:1412.6980, 2014.
[Kingma and Welling, 2013] Diederik P Kingma and Max
Welling. Auto-encoding variational bayes. arXiv preprint
arXiv:1312.6114, 2013.
[Kleinberg, 2003] Jon Kleinberg. Bursty and hierarchical
structure in streams. Data Mining and Knowledge Discovery, 7(4):373–397, 2003.
[Li et al., 2017] Jundong Li, Harsh Dani, Xia Hu, Jiliang
Tang, Yi Chang, and Huan Liu. Attributed network embedding for learning in a dynamic environment. In Proceedings
of the 2017 ACM on Conference on Information and Knowledge Management, pages 387–396. ACM, 2017.
[Mikolov et al., 2013] Tomas Mikolov, Ilya Sutskever, Kai
Chen, Greg S Corrado, and Jeff Dean. Distributed representations of words and phrases and their compositionality. In
Advances in neural information processing systems, pages
3111–3119, 2013.
[Mitchell and Beauchamp, 1988] Toby J Mitchell and John J
Beauchamp. Bayesian variable selection in linear regression. Journal of the American Statistical Association,
83(404):1023–1032, 1988.
[Nguyen et al., 2018] Giang Hoang Nguyen, John Boaz Lee,
Ryan A Rossi, Nesreen K Ahmed, Eunyee Koh, and
Sungchul Kim. Continuous-time dynamic network embeddings. In Companion of the The Web Conference 2018
on The Web Conference 2018, pages 969–976. International
World Wide Web Conferences Steering Committee, 2018.
[Parikh and Sundaresan, 2008] Nish Parikh and Neel Sundaresan. Scalable and near real-time burst detection from
ecommerce queries. In Proceedings of the 14th ACM
SIGKDD international conference on Knowledge discovery
and data mining, pages 972–980. ACM, 2008.
[Perozzi et al., 2014] Bryan Perozzi, Rami Al-Rfou, and
Steven Skiena. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD
international conference on Knowledge discovery and data
mining, pages 701–710. ACM, 2014.
[Qiu et al., 2018] Jiezhong Qiu, Yuxiao Dong, Hao Ma, Jian
Li, Kuansan Wang, and Jie Tang. Network embedding
as matrix factorization: Unifying deepwalk, line, pte, and
node2vec. In WSDM, pages 459–467. ACM, 2018.
[Trivedi et al., 2017] Rakshit Trivedi, Hanjun Dai, Yichen
Wang, and Le Song. Know-evolve: Deep temporal reasoning for dynamic knowledge graphs. In Proceedings of
the 34th International Conference on Machine LearningVolume 70, pages 3462–3471. JMLR. org, 2017.
[Wang et al., 2016] Daixin Wang, Peng Cui, and Wenwu Zhu.
Structural deep network embedding. In KDD, pages 1225–
1234. ACM, 2016.
[Zhou et al., 2018] Lekui Zhou, Yang Yang, Xiang Ren, Fei
Wu, and Yueting Zhuang. Dynamic network embedding by
modeling triadic closure process. 2018.
[Zhu et al., 2016] Linhong Zhu, Dong Guo, Junming Yin,
Greg Ver Steeg, and Aram Galstyan. Scalable temporal
latent space inference for link prediction in dynamic social networks. IEEE Transactions on Knowledge and Data
Engineering, 28(10):2765–2777, 2016.