C语言-最短路径(Floyd算法)
- 顶点下标查找函数(LocateVex)
- 创建有向网(CreateDN)
- 打印图函数(print)
- 弗洛伊德算法(ShortestPath_Floyd)
- 展示最短路径(DisplayPath)
多源点最短路径
- 多源点意为多起始点,也就是图中所有顶点都将作为起始点,求此顶点到达图中其他所有顶点的最短路径
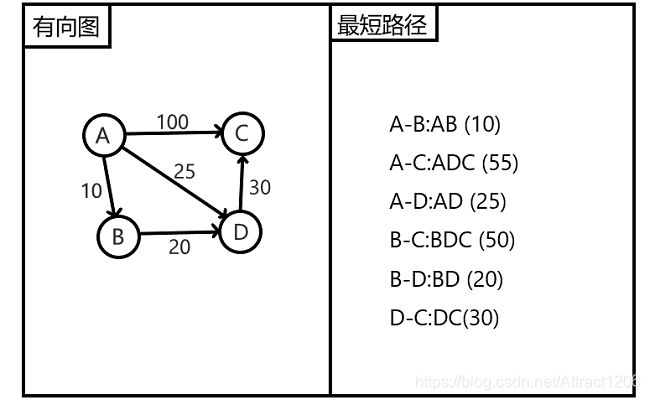
(未展示出不可达边!下列所有代码的测试数据均是此有向图!) - 在之前学习的Dijskra算法,我们知道Dijskra算法是求解单源点最短路径的算法,使用Dijskra算法可以求出一个源点到其他所有顶点的最短路径,那么我们将Dijskra算法循环执行n次(n为顶点数),每次带入图中的一个顶点,不就实现了求解多源最短路吗?
- Dijskra算法执行单次的时间复杂度为O(n2),其中n为顶点个数,循环执行n次,那么使用Dijskra算法求解多源点最短路径的整体时间复杂度为O(n3)
- 此次我们引入的求解多源点最短路径问题的算法是——Floyd算法,时间复杂度也为O(n3),但是在算法构造和算法可读性上优于执行n次的Dijskra算法。
Floyd算法思想
- 弗洛伊德的核心思想是:对于网中的任意两个顶点(例如顶点 A 到顶点 B)来说,之间的最短路径不外乎有 2 种情况:
- 直接从顶点 A 到顶点 B 的边的权值为顶点 A 到顶点 B 的最短路径。
- 从顶点 A 开始,经过若干个顶点,最终达到顶点 B,期间经过的边的权值和为顶点 A 到顶点 B 的最短路径。
- 所以,弗洛伊德算法的核心为:对于从顶点 A 到顶点 B 的最短路径,拿出网中所有的顶点进行如下判断:
Dist(A,K)+ Dist(K,B)< Dist(A,B)
其中,K 表示网中所有的顶点;Dist(A,B) 表示顶点 A 到顶点 B 的距离 - 也就是说,拿出所有的顶点 K,判断经过顶点 K 是否存在一条可行路径比直达的路径的权值小,如果式子成立,说明确实存在 一条权值更小的路径,此时只需要更新记录的权值和即可。
Floyd算法
- 本人在对书上(严蔚敏数据结构第二版C语言版)原版Floyd代码(1.0版本)的基础上,对path数组结构进行了修改,写出了后续2.0版本和3.0版本
1.0版本(书上原版):path存储终点的前驱
int dist[VertexMax][VertexMax];
int path[VertexMax][VertexMax];
void ShortestPath_Floyd(MGraph G)
{
int i,j,k;
//初始化部分
for(i=0;i<G.vexnum;i++)
{
for(j=0;j<G.vexnum;j++)
{
dist[i][j]=G.AdjMatrix[i][j];
if(dist[i][j]!=MaxInt)
{
path[i][j]=i;//存入前驱
}
else path[i][j]=-1;
}
}
//Floyd算法核心部分
for(k=0;k<G.vexnum;k++)//拿出每个顶点作为遍历条件
for(i=0;i<G.vexnum;i++)
for(j=0;j<G.vexnum;j++)
{
if(dist[i][j]>dist[i][k]+dist[k][j])
{
dist[i][j]=dist[i][k]+dist[k][j];
path[i][j]=path[k][j];//存入前驱
}
}
}
- 此时的path数组是一个整型二维数组,存储的内容是该条路径终点的前驱顶点
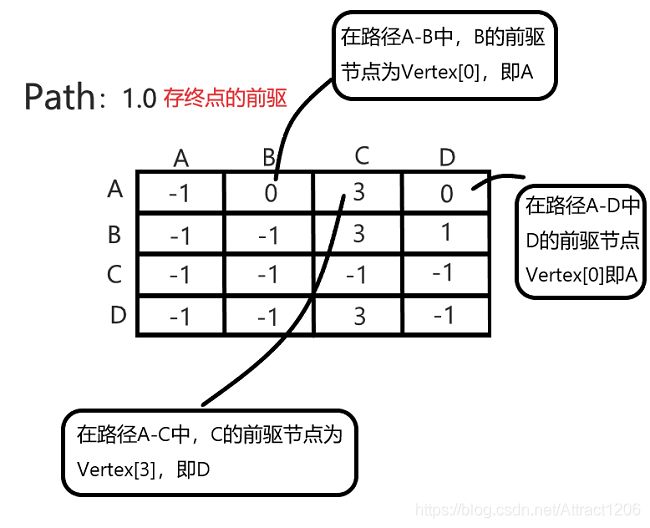
- 1.0版本的path数组存储,与Dijskra的path数组存储类型一致,都是存储前驱顶点,这样存储的结果最终是不能直接得到最短路径的,直接输出是逆序的(请看执行结果1.0),我们需要用一个数组先存储,再逆序输出。为了解决这个问题,我写出了2.0版本
2.0版本:path存储起点的后继
int dist[VertexMax][VertexMax];
int path[VertexMax][VertexMax];
void ShortestPath_Floyd(MGraph G)
{
int i,j,k;
//初始化部分
for(i=0;i<G.vexnum;i++)
{
for(j=0;j<G.vexnum;j++)
{
dist[i][j]=G.AdjMatrix[i][j];
if(dist[i][j]!=MaxInt)
{
path[i][j]=j;//存入后继
}
else path[i][j]=-1;
}
}
//算法核心部分
for(k=0;k<G.vexnum;k++)//拿出每个顶点作为遍历条件
for(i=0;i<G.vexnum;i++)
for(j=0;j<G.vexnum;j++)
{
if(dist[i][j]>dist[i][k]+dist[k][j])
{
dist[i][j]=dist[i][k]+dist[k][j];
path[i][j]=path[i][k];//存入后继
}
}
}
- 此时path数组仍是二维整型数组,存储的是该条路径起点的后继顶点
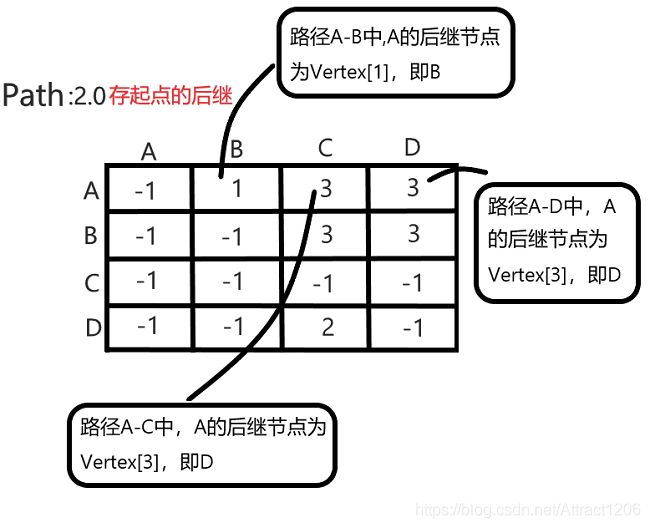
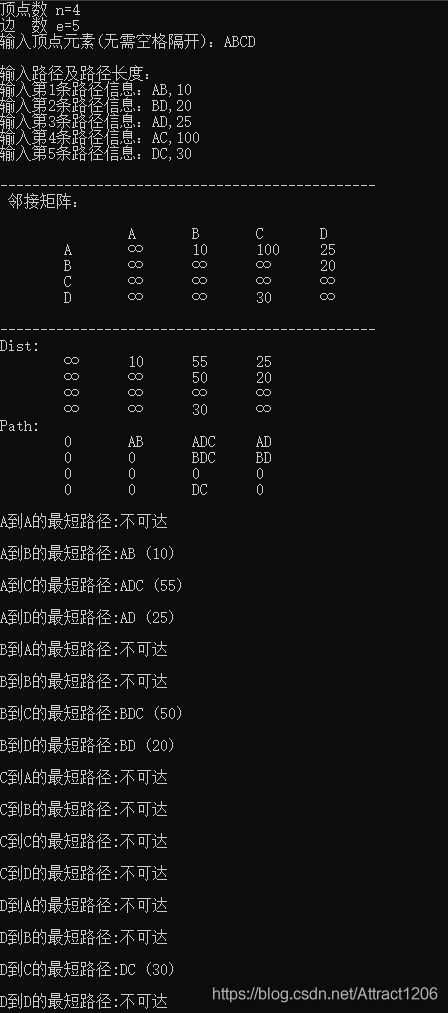
- 2.0版本的path数组存储的是当前顶点的后继,那么就可以顺着起始点,顺序一个个找到终点,这种存储方式是可以顺序输出的(请看执行结果2.0)
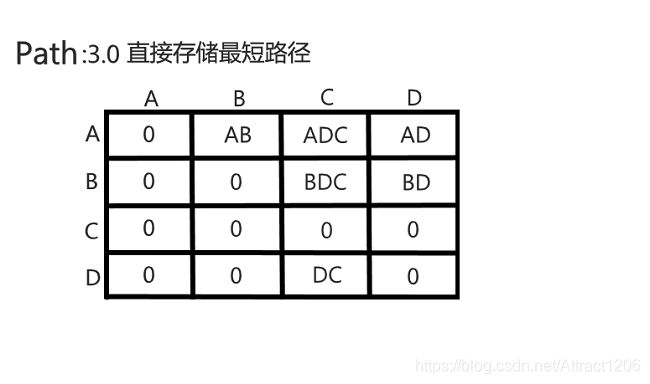
3.0版本:在path中直接存入最短路径
int dist[VertexMax][VertexMax];
VertexType path[VertexMax][VertexMax][VertexMax]; //三维数组
char *NewPath(char temp1[VertexMax],char temp2[VertexMax])
{
int i=0;
static char ch1[VertexMax],ch2[VertexMax];//要定义成静态变量
for(i=0;i<VertexMax;i++)
{
ch1[i]=temp1[i];
ch2[i]=temp2[i];
}
i=0;
while(ch1[i]!='\0')
{
i++;
}
if(ch1[i-1]!=ch2[0])
{
strcpy(&ch1[i],&ch2[0]);
}
else if(ch1[i-1]==ch2[0])
{
strcpy(&ch1[i-1],&ch2[0]);
}
return ch1;
}
void ShortestPath_Floyd(MGraph G)
{
int i,j,k;
char temp1[2]="0",temp2[2]="0";
//初始化部分
for(i=0;i<G.vexnum;i++)
{
for(j=0;j<G.vexnum;j++)
{
dist[i][j]=G.AdjMatrix[i][j];
if(dist[i][j]!=MaxInt)
{
temp1[0]=G.Vertex[i];
temp2[0]=G.Vertex[j];
strcpy(path[i][j],NewPath(temp1,temp2));
}
else strcpy(path[i][j],"0");
}
}
//算法核心部分
for(k=0;k<G.vexnum;k++)//拿出每个顶点作为遍历条件
for(i=0;i<G.vexnum;i++)
for(j=0;j<G.vexnum;j++)
{
if(dist[i][j]>dist[i][k]+dist[k][j])
{
dist[i][j]=dist[i][k]+dist[k][j];
strcpy(path[i][j],NewPath(path[i][k],path[k][j]));
}
}
}
-
要实现path直接存储最短路径(字符串),还需要写一个字符串合并函数NewPath,该函数实现的功能是:
①初始时AB之间有边,传入A、B将其合成为"AB"
② 后续如果有形如:AB、BC可以合成为AC -
需要注意的是:
① 初始化时,G.Vertex[i]与G.Vertex[j],要先放入字符数组temp1和temp2,以字符串的形式传入NewPath函数
② 当字符数组作为函数参数传入时,只能传数组地址,意思就是,此时形参与实参同时指向同一个数组,同时发生改变,所以,要在NewPath函数内定义两个新的数组:
static char ch1[VertexMax],ch2[VertexMax];//要定义成静态变量
来代替作为参数传入的数组进行操作。
总结:
- 三个版本的代码思路基本一致,只有在path数组的构造有些差别
- 通过两次对path数组的升级,让最短路径的生成与存储形式更加直接,更好理解,可视化更强,但避免不了的是3.0版本是最复杂的。
完整源代码:
- 1.0版本:
#include - 2.0版本:
#include - 3.0版本:
#include 执行结果:
参考:
- Floyd算法思想部分参考:数据结构——解学武
- 部分算法思路来自于:西电的小姐姐KittyGirllll
- 部分算法思路来自于:懒猫老师