随机过程基础(5)---各态历经性(2)、联合分布、连续信号功率谱密度（PSD）

各态历经性

可以证明，随机过程X(t)具有均值遍历性的充要条件是$$\underset{Y\to \infty }{\lim }\frac{1}{T}{\int }_0^{2T}(1-\frac{\tau }{2T})[R_X(\tau )-m_X^2]d\tau =0$$具有相关函数遍历性的充要条件是$$\underset{Y\to \infty }{\lim }\frac{1}{T}{\int }_0^{2T}(1-\frac{\tau }{2T})[R_{\varphi }(\tau )-R_X^2(\tau )]d\tau =0$$对于零均值的平稳正态随机信号，如果R_X(τ)连续，则各态历经性的充要条件简化为$${\int }_0^{\infty }|R_X(\tau )|d\tau <\infty$$
例如，判断随机相位信号的各态历经性：
设有随机相位信号$$X(t)=Acos({\omega }_{0}t+\varphi )$$则X(t)的均值为0，自相关函数$$R_X(t+\tau ,t)=E[X(t+\tau )X(t)]$$$$=A^{2}E\{cos[{\omega }_0(t+\tau )+\varphi ]cos({\omega }_{0}t+\varphi )\}$$应用积化和差公式，$$=\frac{A^2}{2}\{E[cos(2{\omega }_{0}t+{\omega }_o\tau +2\varphi )]+E[cos{\omega }_0\tau ]\}$$$$=\frac{A^2}{2}cos{\omega }_0\tau$$又时间平均$$\overline{m_X}=1\cdot i\cdot m\frac{1}{2T}{\int }_{-T}^{T}Acos({\omega }_0+\varphi )dt=0$$时间相关函数$$\overline{R_X(\tau )}=1\cdot i_{T\to \infty }\cdot m\frac{1}{2T}{\int }_{-T}^{T}X(t+\tau )X(t)dt$$$$=1\cdot i_{T\to \infty }\cdot m\frac{1}{2T}{\int }_{-T}^{T}Acos[{\omega }_0(t+\tau )+\varphi ]Acos({\omega }_{0}t+\varphi )dt$$$$=\frac{A^2}{2}1\cdot i_{T\to \infty }\cdot m\frac{1}{2T}{\int }_{-T}^T[cos(2{\omega }_{0}t+{\omega }_0\tau +2\varphi )+cos({\omega }_0\tau ]dt$$$$=\frac{A^2}{2}cos{\omega }_0\tau$$故时间量和统计量两两对应相等，可见是各态历经过程。
对于大多数随机过程，都具有各态历经性。工程上一般直接认为平稳随机信号是各态历经的。设x(t)是一条样本函数，就用$$\widehat{m_X}=\frac{1}{2T}{\int }_{-T}^{T}x(t)dt$$估计均值，用$${\hat{R}}_X(\tau )=\frac{1}{2T}{\int }_{-T}^{T}x(t+\tau )x(t)dt$$估计自相关函数，得到的结果差距不大。
对于随机序列X(n)，对应地，$$\widehat{m_X}=\frac{1}{N}\sum _{N=0}^{N-1}x(n)$$$$\widehat{{\sigma }_X^2}=\frac{1}{N-1}\sum _{n=0}^{N-1}[x(n)-{\hat{m}}_X{]}^2$$$$\widehat{R_X(m)}=\frac{1}{N-|m|}\sum _{n=0}^{N-|m|-1}x(n)x(n+m)$$其中m取整数。

联合分布函数和联合概率密度

设随机过程X(t)有N维概率分布，Y(t)有M维概率分布，X(t) Y(t)N+M维联合概率分布函数$$F_{XY}(x_1,...,x_N,t_1,...t_N,y_1,...y_M,t_1^{\prime },...t_M^{\prime })$$$$=P\{X(t_1)\le x_1,...,X(t_N)\le x_N,Y(t_1^{\prime })\le y_1,...,Y(t_M^{\prime })\le y_M\}$$相似地，N+M维联合概率密度就是求N+M阶偏导（x N阶，y M阶）。如果任意联合概率分布可以直接乘开成x的边缘概率分布和y的边缘概率分布之积，就称X(t)与Y(t)相互独立。如果联合统计特性不随时间起点的平移而变化，则称两者联合联合平稳，或称平稳相依。这时，有$$f_{XY}(x_1,...,x_N,t_1,...t_N,y_1,...y_M,t_1^{\prime },...t_M^{\prime })$$$$=f_{XY}(x_1,...,x_N,t_1+c,...t_N+c,y_1,...y_M,t_1^{\prime }+c,...t_M^{\prime }+c)$$互相关函数定义为$$R_{XY}(t_1,t_2)=E[X(t_1)Y(t_2)]={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }xy{f}_X(x,t_1,y,t_2)dxdy$$互协方差函数$$K_{XY}(t_1,t_2)=E\{E[X(t_1)-E(X(t_1))][E(Y(t_2)-E(Y(t_2))]\}$$同样地，$$K_{XY}(t_1,t_2)=R_{XY}(t_1,t_2)-m_X(t_1)m_Y(t_2)$$同样地，$R_{XY}(t_1,t_2)=0$，两随机过程相互正交，$K_{XY}(t_1,t_2)=0$，两随机过程不相关。独立一定不相关，不相关不一定独立。

多维随机变量的分布、单个随机过程的分布、多个随机过程的联合分布之间的关系

单个随机过程每一时刻都包含某个随机变量，所以单个随机过程可以看作无穷维的随机变量。拿出来一个时刻，得到的叫一维概率分布，完全等于一个随机变量，可以做的事情是求概率分布、概率密度、均值、方差、二阶矩。拿出来两个时刻，得到的叫二维概率分布，不考虑时间性质就等于二维随机变量可以求的是二维概率分布、二维分布函数，一维中的二阶原点矩这里相当于（自）相关函数，相当于求的是两者乘积的均值；一维中的方差这里相当于协方差函数。与单纯的二维不同的是，两个时刻如果取到了一个地方，就对应回了一维的情况。多维也是如此，但是高维对应的统计函数几乎不做要求。考虑时间性质，就是考虑了每个时刻（相当于随机变量）的统计特性随时间变化的情况。利用一些特殊过程中随机变量特征（均值、方差）随时间的不变性，引入平稳随机过程和它的变体。两者之间的桥梁是，

各态历经的平稳过程中用时间轴上平均的结果可以估计平稳过程一些不变的统计量。

功 率 谱（重点）

先把信号与系统中时频转换的知识复习一遍。数学中，相当于已经证明了周期信号的傅里叶变换：
三角函数系具有正交性：(指两信号内积为0)，而且是完备的（不存在任何能量有限的、与正交函数集内所有基底信号正交的信号）。与完备性等价的概念有：完全性、收敛性、张成子空间为全空间、转换后的信号与原信号满足Parseval等式。
$${\int }_{-\pi }^{\pi }sinkxsinnxdx=0$$$${\int }_{-\pi }^{\pi }sinkxcosnxdx=0$$$${\int }_{-\pi }^{\pi }coskxcosnxdx=0$$k,n取整数，且k,n不相等。上三式均通过积化和差公式证明。而$${\int }_{-\pi }^{\pi }si{n}^{2}nxdx=\pi$$$${\int }_{-\pi }^{\pi }co{s}^{2}nxdx=\pi$$n取到正整数。假设周期为2pi的函数f(x)能展开成$$f(x)=\frac{a_0}{2}+\sum _{k=1}^{\infty }(a_{k}coskx+b_{k}sinkx)$$对左右两端从-pi到+pi积分，有$$\pi a_0={\int }_{-\pi }^{\pi }f(x)dx$$对左右两端同乘cos nx，结合上方给出的正交性，除coas kx中k=n的一项外，全部sin kx cos k(!=n)*x全部为0$${\int }_{-\pi }^{\pi }f(x)cosnxdx=a_n{\int }_{-\pi }^{\pi }co{s}^{2}nxdx=a_n\pi$$得到$$a_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)cosnxdx$$同理$$b_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)sinnxdx$$同理可以推出，对于周期为2l的周期函数，傅里叶级数展开成$$f(x)=\frac{a_0}{2}+\sum _{k=1}^{\infty }(a_{k}cos\frac{n\pi x}{l}+b_{k}sin\frac{n\pi x}{l})$$$$a_n=\frac{1}{l}{\int }_{-l}^{l}f(x)cos\frac{n\pi x}{l}dx$$$$b_n=\frac{1}{l}{\int }_{-l}^{l}f(x)sin\frac{n\pi x}{l}dx$$在数学中，应该满足狄利克雷展开条件（一个周期内绝对可积、有有限个第一类间断点和极值点，或根本没有，以保证黎曼可积）。针对有间断点的情况，f(x)代入的应是$$f(x)=\frac{1}{2}[f(x^{-})+f(x^{+})]$$

对于$$f(x)=\frac{a_0}{2}+\sum _{k=1}^{\infty }(a_{k}cos\frac{n\pi x}{l}+b_{k}sin\frac{n\pi x}{l})$$工程上通常用另一组完备正交信号集----虚指数信号集代替表示。先有复数域（复变函数）的基础：欧拉公式$$e^{ix}=cosx+isinx$$
虚指数信号集是$$e^{jn\Omega t},n取所有整数。$$它在(t,t+T)上是完备正交的。对完备正交性，证明如下：（*代表共轭信号。证明完备性，是等价转换成帕斯瓦尔定理来证的）

在虚指数信号集上展开(t0,t0+T)，效果是$$f(t)=\sum _{k=-\infty }^{\infty }{F}_k{e}^{jk\Omega t}$$其中，$$F_k=\frac{1}{T}{\int }_{t_0}^{t_0+T}f(t)e^{-jk\Omega t}dt$$推导是$$F_k=\frac{<f(t),{\varphi }_k(t)>}{<{\varphi }_k(t),{\varphi }_k(t)>}$$$$=\frac{{\int }_{t_0}^{t_0+T}f(t)e^{-jk\Omega t}dt}{{\int }_{t_0}^{t_0+T}{e}^{jk\Omega t}{e}^{-jk\Omega t}dt}$$$$=\frac{1}{T}{\int }_{t_0}^{t_0+T}f(t)e^{-jk\Omega t}dt$$
根据欧拉公式，容易证明三角形式傅里叶展开和指数形式傅里叶展开是等价的。两者在形式上不同，指数形式计算机运算往往要简单不少；两者在幅度相位图上，一个（先转换成余弦级数）是 c ~ w,phi ~ w的单边幅度相位谱；一个是（先将F _n虚实分开）|F| ~ w, phi ~ w的双边幅度相位谱。
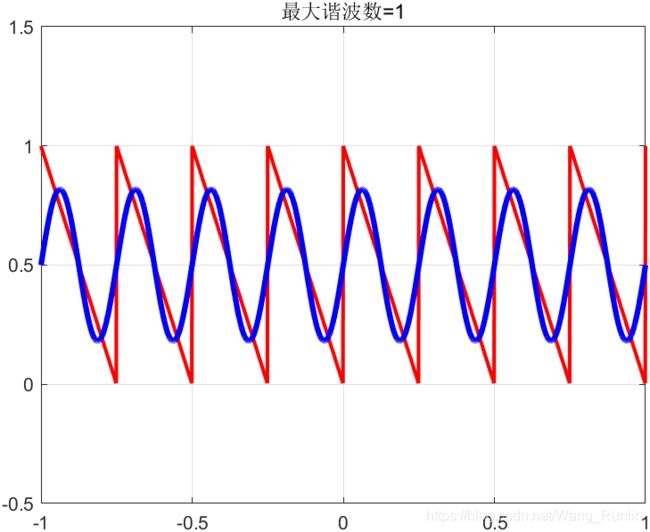
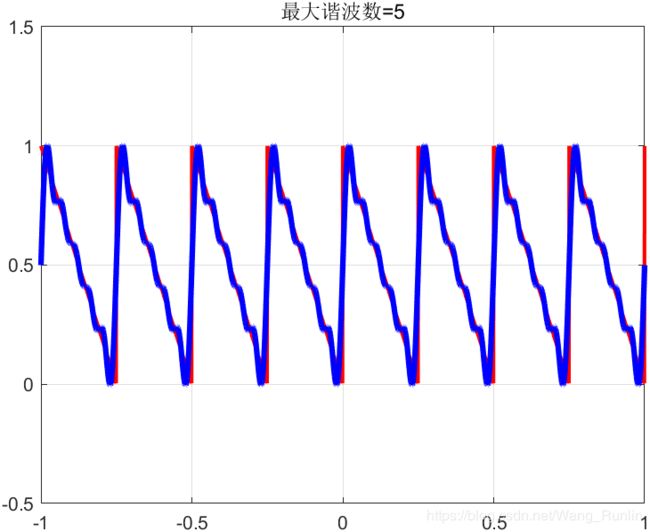
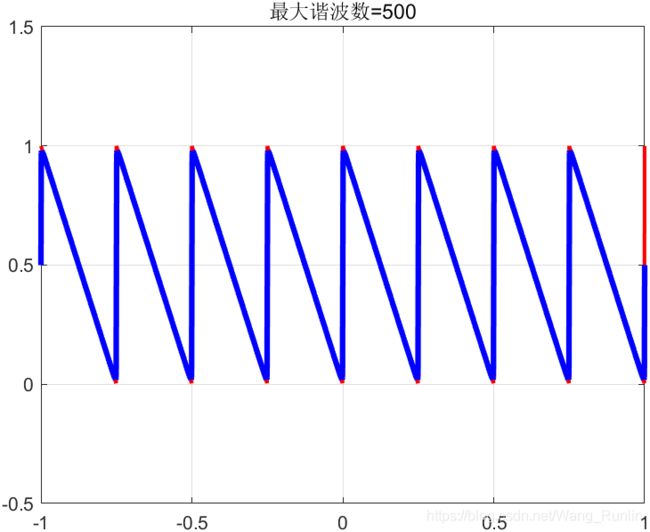
如下，用matlab模拟一下正余弦信号使谐波数k逐渐增大，是如何锯齿波信号的：

t = -1:0.001:1;
w0 = 8*pi;
y = -1/2 * (-1+sawtooth(8*pi*t))%周期为2的锯齿波信号
% 锯齿波信号的傅里叶级数%
plot(t,y,'k','linewidth',4), grid on;
axis([-1 1 -0.5 1.5]);
n_max = [1 3 5 7 500];
N = length(n_max);
for k = 1:N
    n = 1:1:n_max(k);
    b = 1./(pi*n);
    x = 1/2 + b * sin(w0*n'*t);
    figure;
    plot(t,y,'r','linewidth',2);    hold on;
    plot(t,x,'b','linewidth',3);    hold off;
    axis([-1 1 -0.5 1.5]),grid on;
     title(['最大谐波数=',num2str(n_max(k))]);
end

以上是周期信号的傅里叶分解，必须满足狄利克雷条件。但引入冲激函数后，不满足的也可以展开，所以它只是充分条件。以下给出由周期形式傅里叶展开引入非周期的傅里叶变换的过程（非周期信号可看作周期为无穷大的信号）。
————————
_{以下图片来自《信号与系统》课件。}



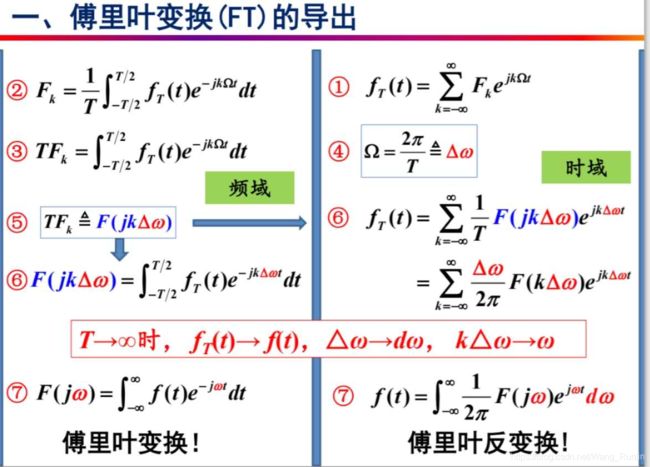
上述推导的关键步骤是，当取的周期趋于无穷大时，ω就变得很小，将T变化映射到ω变化，那么将ω极微小的变化量改写成微元量、kΔω相当于把ω肢解后的各成分重新合在一起；另一方面，T趋于无穷时的周期信号就可以看作就是原信号了。最终得到傅里叶变换$$F(j\omega )={\int }_{-\infty }^{\infty }f(t)e^{-j\omega t}dt$$
和反变换
$$f(t)={\int }_{-\infty }^{\infty }\frac{1}{2\pi }F(j\omega )e^{j\omega t}d\omega$$

将信号的总能量表示为$$E={\int }_{-\infty }^{\infty }{f}^2(t)dt$$
时域总能量等于频域总能量：$$E={\int }_{-\infty }^{\infty }{f}^2(t)dt={\int }_{-\infty }^{\infty }\frac{1}{2\pi }|F(j\omega ){|}^{2}d\omega$$若总能量$$E={\int }_{-\infty }^{\infty }{f}^2(t)dt$$有限，则称为能量有限信号。一般的随机过程都不会是能量有限的，因为它往往铺满整个时间轴。但实际中它的平均功率总是有限的。$$P=\underset{T\to \infty }{\lim }\frac{1}{2T}{\int }_{-\infty }^{\infty }|x(t){|}^{2}dt<\infty$$所以引入功率谱
定义截尾函数$$x_{Ti}(t)$$让它在|t|$$X_{Ti}(\omega )={\int }_{-T}^T{x}_i(t)e^{-j\omega t}dt$$$$x_{Ti}(t)={\int }_{-\infty }^{\infty }\frac{1}{2\pi }{X}_{Ti}(j\omega )e^{j\omega t}d\omega$$
样本函数平均功率$$P_i=\underset{T\to \infty }{\lim }\frac{1}{2T}{\int }_{-\infty }^{\infty }|x_i(t){|}^{2}dt$$
$$=\underset{T\to \infty }{\lim }\frac{1}{2T}{\int }_{-\infty }^{\infty }\frac{1}{2\pi }|X_{Ti}(\omega ){|}^{2}d\omega$$
$$=\underset{T\to \infty }{\lim }\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{1}{2T}|X_{Ti}(\omega ){|}^{2}d\omega$$
令$$G_i(\omega )=\frac{1}{2T}|X_{Ti}(\omega ){|}^2$$则$$P_i=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{G}_i(\omega )d\omega$$$G_i(\omega )=\frac{1}{2T}|X_{Ti}(\omega ){|}^{2}d\omega$称为x_i(t)的功率谱密度。
从上可见，功率谱密度也是从某一个样本函数计算的，所以它也是随机的。那就不妨在式子了加一个变量表示功率谱用的哪个样本函数算的（避免混淆，这里加e）$$X_T(\omega ,e)={\int }_{-T}^T{x}_i(t,e)e^{-j\omega t}dt$$
把它也加到平均功率去
$$P(e)=\underset{T\to \infty }{\lim }\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{1}{2T}|X_T(\omega ,e){|}^{2}d\omega$$交换积分和极限，把常数拿到外面，然后执行如下操作：

那么$$E[G_i(\omega )]=E[\frac{1}{2T}|X_T(\omega ){|}^{2}d\omega ]$$就定义为随机过程的功率谱密度。当然，$$X_T(\omega )={\int }_{-T}^{T}X(t)e^{-j\omega t}dt$$这里较最初的$X_{Ti}(\omega )={\int }_{-T}^T{x}_i(t)e^{-j\omega t}dt$少了i，表示不是第i条样本函数的频谱；小写的x改成大写，表示它不是某一次的样本函数，而是泛指整个随机过程。
功率谱密度在电路中的意义：单位频带内信号的频谱分量消耗在单位电阻上的平均功率的统计平均值。G（ω）函数从频域角度描述了X（t）的统计特征，但是不包含X（t）的相位信息。

可以证明，对于平稳随机过程，如果相关函数与时间差的乘积绝对可积，那么其相关函数和功率谱之间是傅里叶变换对的关系，这一结果叫维纳-辛钦定理。

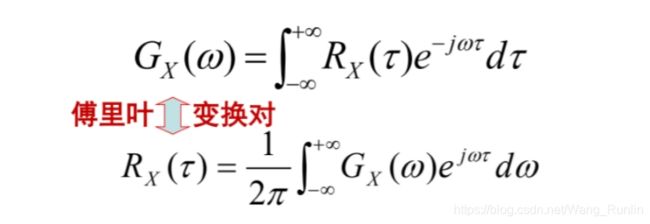
就像刚才推导周期信号展开成傅里叶级数引入δ函数就可适用于不满足狄利克雷条件的信号，相关函数与功率谱密度中，如果引入δ函数，相关函数和时间差的乘积不绝对可积的信号也可以转换成功率谱的形式。
这里列举信号与系统中傅里叶变换对的性质，当然也适用于这对，并且给出当时难理解性质的证明：

1. 唯一性：确定信号的傅里叶变换是唯一的

2. 线性特性：af（t）+bf （t）<-> aF（ jω）+ bF（ jω）

3. 奇偶特性：偶信号的频谱是偶函数，奇信号的频谱是奇函数。平稳随机过程的相关函数是偶函数，因此平稳随机过程的功率谱是实的、非负的偶函数。

4. 共轭特性： f(t)<->F(jω) f*(t)<->F*(-jω)

5. 对称特性：(重点）

6. 时域展缩特性：$$f(at)<->\frac{1}{|a|}F(j\frac{\omega }{a})$$

7. 时移特性：$$f(t-t_0)<->F(j\omega )e^{-j\omega t_0}$$

8. 频移特性：$$f(t)e^{j\omega t_0}<->F[j(\omega -{\omega }_0)]$$

9. 时域微分特性：

10. 频域微分特性：$$tf(t)<->j\frac{d}{d\omega }F(j\omega )$$

11. 时域卷积定理（重点）$$f(t_1)\ast f(t_2)<->F(j{\omega }_1)\cdot F(j{\omega }_2)$$

12. 频域卷积定理（重点）$$f_1(t)\cdot f_2(t)<->\frac{1}{2\pi }F(j{\omega }_1)\ast F(j{\omega }_2)$$

13. 时域积分定理

14. 信号能量与频谱关系，也即前述帕斯瓦尔等式$${\int }_{-\infty }^{\infty }{f}^2(t)dt={\int }_{-\infty }^{\infty }\frac{1}{2\pi }|F(j\omega ){|}^{2}d\omega$$
    在今后，就在频域分析基础上计算功率谱。下面给出典型随机过程的相关函数和功率谱，推导详见信号与系统，这里记住直接用。

对于傅里叶反变换$$R_X(\tau )=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{G}_X(\omega )e^{j\omega \tau }d\omega$$τ取到0时，$$R_X(0)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{G}_X(\omega )d\omega$$这说明总的平均功率等于功率谱密度在整个频率轴上的积分
又负频率在现实中不存在（在理解中存在）所以又定义物理功率谱$$F_X(\omega )=2G_X(\omega ),\omega \ge 0$$ω小于0时值取0。那么$$F_X(\omega )=4{\int }_0^{\infty }{R}_X(\tau )cos\omega \tau d\tau$$$$R_X(\tau )=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{F}_X(\omega )cos\omega \tau d\omega$$这里举一例，用平稳随机过程的功率谱求自相关函数。已知功率谱$$G_X(\omega )=\frac{{\omega }^2+4}{{\omega }^4+10{\omega }^2+9}$$求自相关函数：
按照传统的解法，自然是因式分解、套用上面的常见傅里叶变换对套地解。这里用matlab解：

>> syms w t;
Fw=(w^2+4)/(w^4+10*w^2+9);
ft=ifourier(Fw,w,t);
>> pretty(ft);

得出结果

与因式分解结果一致。相关函数参考
pretty
Fourier transform

上例中为有理谱的形式。事实上，许多平稳过程都具有有理谱的形式，也就是像上面答案中的分式形式，注意都是以ω²出现。分母阶数应高于分子阶数，等项为p级数相差在2以上，保证了收敛性；根据平稳随机过程的功率谱为非负实偶函数，那么分母多项式一定没有实根。$$G_X(\omega )=c_0^2\frac{{\omega }^{2n}+a_{2(N-1)}{\omega }^{2(n-1)}+...+a_2\omega ＾2+a_0}{{\omega }^{2M}+b_{2(M-1)}{\omega }^{2(M-1)}+...+b_0}$$其中n>=M，一定可以分解成分母的根都是虚根的两项之积的形式。$$c_0\frac{(-j\omega +{\alpha }_1)(-j\omega +{\alpha }_2)...(-j\omega +{\alpha }_N)}{(-j\omega +{\beta }_1)(-j\omega +{\beta }_2)....(-j\omega +{\beta }_M)}\cdot c_0\frac{(j\omega +{\alpha }_1)(j\omega +{\alpha }_2)...(j\omega +{\alpha }_N)}{(j\omega +{\beta }_1)...(j{\omega }_0+{\beta }_M)}$$
这就给拉普拉斯变换带来便利。设$$G_X^{+}(\omega )=c_0\frac{(-j\omega +{\alpha }_1)(-j\omega +{\alpha }_2)...(-j\omega +{\alpha }_N)}{(-j\omega +{\beta }_1)(-j\omega +{\beta }_2)....(-j\omega +{\beta }_M)}$$$$G_X^{-}(\omega )=c_0\frac{(j\omega +{\alpha }_1)(j\omega +{\alpha }_2)...(j\omega +{\alpha }_N)}{(j\omega +{\beta }_1)...(j{\omega }_0+{\beta }_M)}$$将jω换为s，就得到拉普拉斯变换表示。

——————————
_{部分公式源自
《信号与系统分析》，吴京等著，国防科技大学出版社；《高等数学》，周建莹等著，北京大学出版社；《复变函数》，西安交通大学数学教研组著，高等教育出版社；《随机信号分析与处理》，罗鹏飞等著，清华大学出版社}