【在线笔试题解题报告系列】Google APAC 2017 University Test Round E
最后一轮的 2017 Google APAC Test 了呢。
scoreboard中搜索hdu.toraoh,可以看我的当时实际提交情况。
照惯例,题意就不翻译了。(毕竟Google有英文面试的)
本文URLhttp://blog.csdn.net/fcxxzux/article/details/53055195,转载请留地址(而且现在还没完工呢)
A. Diwali lightings
显然要利用这个模式串s很短,查询区间很长。
我们知道查询区间里s完整地出现几次,再补上最开头s的末尾一部分,再补上最后s的开头一部分,这3部分的B的数量之和,完事。
能写起来更简单吗?
对于这种求 [a,b] 之间满足一定条件的东西的数目的题目,我们可以做以下的转化:
[a,b]的答案=[1,b]的答案−[1,a]的答案
而[1,a]的答案,在处理的时候,就没有要补上s尾部一块的问题了。
(所以我就是这么写的)
#include if(s[i]=='B'){
ans+=d;
if(i1;
}
}
return ans;
}
int main(){
freopen("A-large.in","r",stdin);
freopen("A-large.out","w",stdout);
int T,Case=1;
for(scanf("%d",&T);Case<=T;Case++){
scanf("%s%I64d%I64d",s,&a,&b);
printf("Case #%d: %I64d\n",Case,cnt(b)-cnt(a-1));
}
return 0;
}
B. Beautiful Numbers
考虑做的方向:
先进制再确定长度?
不行,进制可行解多,范围极大,还不连续,没法直接二分进制求得答案。
那先确定长度再考虑几进制?
因为2^64>10^18,2进制下都不可能长度超过64位,好像可行。
那怎么确定是几进制的呢?
A、二分,不是超了就是少了,或者刚好,还是单调变化,非常好
B、为什么不直接开根号呢?
对输入的 n ,从最长的长度 x 枚举,直接开 (x−1) 次根号并下取整,然后代回检查。
直接开根号可行的解释的话。
首先,我们要知道,
对 b 进制的数 (12345)b ,转成10进制,要这么算:
1∗b4+2∗b3+3∗b2+4∗b1+5∗b0
然后反证法:
假设长度x的情况下,开根号,告诉你应该是b进制
先证明不可能是b-1进制
b-1进制的情况下,这个数如果各个位置全1,转化成10进制,应该是:
1∗(b−1)x−1+⋯+1∗(b−1)3+1∗(b−1)2+1∗(b−1)1+1∗(b−1)0
我们来把 bx−1 变形一下:
bx−1
=((b−1)+1)x−1
=(x−1x−1)(b−1)x−1+(x−1x−2)(b−1)x−2+… (二项式定理)
>(b−1)x−1+(b−1)x−2+…
然而事实上, bx−1≤n
也就是说, b−1 进制再怎么努力也不行。
b+1 进制也不可能,很直白地能证明:
我们开根号是 n√x−1 ,一个最高位是1,其他位是0的 b+1 进制的数,上来就有 (b+1)x−1>(n√x−1)x−1 ,怎么想都已经虐过那个n了。
或者直接说,开根号和幂次互为逆操作。你开根号的结果再幂回去,一样大。你现在开根号的结果+1再幂回去,肯定大于n了。
所以证明了, ⌊n√x−1⌋ 就是我们想要的(进制)。
当然不要忘了,对长度为2的情况,单独抓出来特判。
#include C. Partioning Number
不妨看成3段:
a0,a0+1,a0+2 3种东西
搞 x,y,z 个,使得 x∗a0+y∗(a0+1)+z∗(a0+2)=n ,而且 a0|d
方法1:
枚举 a0 ,以及到底由几种不同的数组成
1种:直接来,整除检查就行
2种:或者没 y ,得 x∗a0+z∗(a0+2)=n ,或者没 z ,得 x∗a0+y∗(a0+1)=n
3种:枚举x,然后剩下的方程是 y∗(a0+1)+z∗(a0+2)=n−x∗a0
3种二元一次不定方程,求不定方程的整数解的个数的话
掏出扩展欧几里得算法来算吧!
具体可参考欧几里德与扩展欧几里德算法 - jumping_frog - 博客园 的说明,相关细节摘抄如下:
对于不定整数方程 pa + qb = c,若 c mod gcd(a, b) = 0,则该方程存在整数解,否则不存在整数解。(注:以a b c为已知量)
上面已经列出找p * a + q * b = gcd(a, b)一个整数解的方法(扩展欧几里得算法直接求,额外的2个返回值就是p0和q0,我们要的整数解)
在找到p * a+q * b = gcd(a, b)的一组解p0,q0后,
可以得到p * a+q * b = c的一组解
p1 = p0 * ( c / gcd(a,b) ),
q1 = q0 * ( c / gcd(a,b) ),p * a+q * b = c的其他整数解满足:
p = p1 + b / gcd(a, b) * t
q = q1 - a / gcd(a, b) * t(其中t为任意整数)
p 、q就是p * a+q * b = c的所有整数解。
相关证明可参考:
http://www.cnblogs.com/void/archive/2011/04/18/2020357.html
然后,我们要求p>0且q>0,可以得到t的取值范围,
t>−p1∗gcd(a,b)/b
t<q1∗gcd(a,b)/a
其中为整数的t的数量,就是这个二元一次不定方程的正整数解的数量了!
时间复杂度?
外层O(n),最内部求解的数量是O(logn)的
中间枚举 y∗(a0+1)+z∗(a0+2)=n−x∗a0 的时间复杂度呢?
注意到,这里面每层要枚举的数量累加起来为:
n/1+n/2+n/3+⋯+n/n
=nlogn (调和级数)
所以,我们的时间复杂度为 O(nlog2n)
#include 1,i0+2,n-i0*i);
}
}
printf("Case #%d: %I64d\n",Case,ans);
}
return 0;
} 跑完大数据,大约5~10秒。
解法2:by [zucc]ChouUn
(我是真没搞懂,估计是开始的思路就不一样了……
在这里贴一下他的说明和代码)
直接当做3元1次不定方程:
ax+(a+1)y+(a+2)z=n−a…(1)
x+y+z=m−1………………(2)
(其中我们枚举 a 和 m )
(1)−a∗(2) 得
y+2z=(n−a)−a(m−1)
并且补充限制条件 y+z≤m−1
然后画图,可以发现: y+2z 跟 y+z 交点是整点,
不用考虑太多,继续数学一下过了
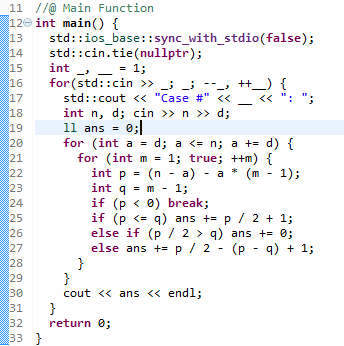
(这个出解很快,真 · O(nlogn) )
D. Sorting Array
目前并不会做(说实话,题都还没读)
有空补上。