SVM cifar-10 cifar-10-batcher-py准确率
总结:SVM在训练cifar-10 测试集的最终结果准确率大概在37%左右
KNN在训练cifar-10测试集的最终结果准确率大概在24%左右
SVM 准确率大于KNN准确率。
$ python3 svm_cifar10.py
datasets/cifar-10-batches-py/data_batch_1
datasets/cifar-10-batches-py/data_batch_2
datasets/cifar-10-batches-py/data_batch_3
datasets/cifar-10-batches-py/data_batch_4
datasets/cifar-10-batches-py/data_batch_5
datasets/cifar-10-batches-py/test_batch
输入交叉验证的任何键...
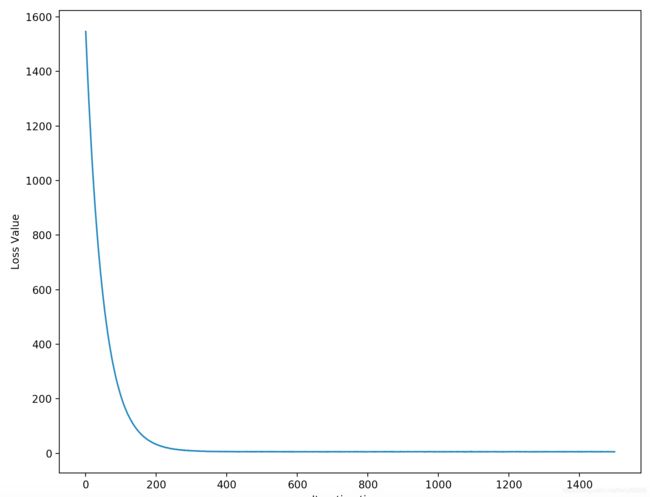
Iteration 0 / 1500: loss 788.809758
Iteration 100 / 1500: loss 288.286786
Iteration 200 / 1500: loss 108.423036
Iteration 300 / 1500: loss 42.809744
Iteration 400 / 1500: loss 19.482382
Iteration 500 / 1500: loss 10.507875
Iteration 600 / 1500: loss 6.682042
Iteration 700 / 1500: loss 6.215942
Iteration 800 / 1500: loss 5.391076
Iteration 900 / 1500: loss 5.342872
Iteration 1000 / 1500: loss 5.252365
Iteration 1100 / 1500: loss 5.057541
Iteration 1200 / 1500: loss 5.435272
Iteration 1300 / 1500: loss 5.255000
Iteration 1400 / 1500: loss 5.081770
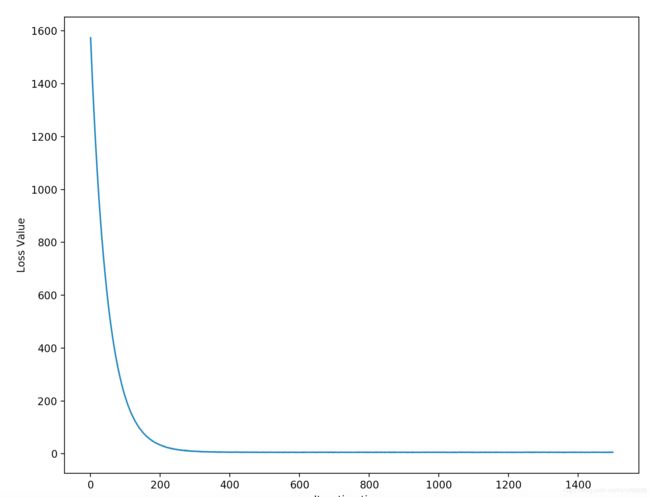
Iteration 0 / 1500: loss 1577.371460
Iteration 100 / 1500: loss 213.065288
Iteration 200 / 1500: loss 32.798858
Iteration 300 / 1500: loss 9.488982
Iteration 400 / 1500: loss 6.239015
Iteration 500 / 1500: loss 5.703100
Iteration 600 / 1500: loss 5.098887
Iteration 700 / 1500: loss 5.999364
Iteration 800 / 1500: loss 5.493077
Iteration 900 / 1500: loss 5.365145
Iteration 1000 / 1500: loss 5.991987
Iteration 1100 / 1500: loss 5.601716
Iteration 1200 / 1500: loss 6.015605
Iteration 1300 / 1500: loss 6.124049
Iteration 1400 / 1500: loss 4.964699
Iteration 0 / 1500: loss 796.187119
Iteration 100 / 1500: loss 424022819942643035248875172947088637952.000000
Iteration 200 / 1500: loss 70087576171176906405554224108021391431082174652295902832401722115289513984.000000
Iteration 300 / 1500: loss 11584915015222530040912623700396874521353404804023631325275062168732329022449235782612823064865026905217171456.000000
Iteration 400 / 1500: loss 1914893669345090862528399726432935809612548877449537311005969364287340502733359299966234927293051604399699550609511013966671137656878155916378112.000000
Iteration 500 / 1500: loss 316516587310284226603510468649229794167103924163906101539857073435711480561666440397966052607017458241845703703145671175475983856441327911157836227156547373870587477942175283544064.000000
Iteration 600 / 1500: loss 52317656925991132337579575061546884525513804433580146888906768530767529044444514624760423878308229456231144122730746688267824470962100780646820541230824812344283326790340890903517743791383665962251774568851415498752.000000
Iteration 700 / 1500: loss 8647689681875871352311044885046354067149086217638760742775822244347750208015820531308569274800157186318181209077255221292545400892659033519201885627689777601075017555268590171889799020194197665060190420174328022834265321146955511092138708959391383552.000000
Iteration 800 / 1500: loss 1429393845749060593011719045074490264519867986143109404134737430885823492664310324156118470701591602170710153567305176862294070086217201166096276316891985061136658827662948327311662756155092741832192294727592893396844789104783455843768805711649040903405266582024531145960423863781163008.000000
/svm.py:89: RuntimeWarning: overflow encountered in double_scalars
loss = np.sum(margins) / num_train + 0.5 * reg * np.sum(self.W * self.W)
/Library/Frameworks/Python.framework/Versions/3.6/lib/python3.6/site-packages/numpy/core/fromnumeric.py:83: RuntimeWarning: overflow encountered in reduce
return ufunc.reduce(obj, axis, dtype, out, **passkwargs)
/Users/apple/work/cs231n/SVM_Cifar10/svm.py:89: RuntimeWarning: overflow encountered in multiply
loss = np.sum(margins) / num_train + 0.5 * reg * np.sum(self.W * self.W)
Iteration 900 / 1500: loss inf
Iteration 1000 / 1500: loss inf
Iteration 1100 / 1500: loss inf
Iteration 1200 / 1500: loss inf
Iteration 1300 / 1500: loss inf
Iteration 1400 / 1500: loss inf
Iteration 0 / 1500: loss 1542.582847
Iteration 100 / 1500: loss 4200537157964490124959388620765546698092510820240820346152324632963133950883343458471047840027329210301522818468608575799296.000000
Iteration 200 / 1500: loss 10846836564053334113704562824411028433288665954090044208738016634694507314675754877281153653141492760616868127534156736031369299490176999006578228663949254535008883142138949629546640288065724156657142776324926439977593736688657018878479665463296.000000
Iteration 300 / 1500: loss inf
Iteration 400 / 1500: loss inf
Iteration 500 / 1500: loss inf
/cs231n/SVM_Cifar10/svm.py:97: RuntimeWarning: overflow encountered in multiply
gred = ground_true.T.dot(X) / num_train + reg * self.W
/cs231n/SVM_Cifar10/svm.py:85: RuntimeWarning: invalid value encountered in maximum
margins = np.maximum(0, margins)
/cs231n/SVM_Cifar10/svm.py:93: RuntimeWarning: invalid value encountered in greater
ground_true[margins > 0] = 1
/cs231n/SVM_Cifar10/svm.py:39: RuntimeWarning: invalid value encountered in subtract
self.W -= learning_rate * gred
Iteration 600 / 1500: loss nan
Iteration 700 / 1500: loss nan
Iteration 800 / 1500: loss nan
Iteration 900 / 1500: loss nan
Iteration 1000 / 1500: loss nan
Iteration 1100 / 1500: loss nan
Iteration 1200 / 1500: loss nan
Iteration 1300 / 1500: loss nan
Iteration 1400 / 1500: loss nan
交叉验证实现的最佳验证精度: 0.372000
Iteration 0 / 1500: loss 780.127495
Iteration 100 / 1500: loss 286.312297
Iteration 200 / 1500: loss 107.822697
Iteration 300 / 1500: loss 42.365619
Iteration 400 / 1500: loss 18.707052
Iteration 500 / 1500: loss 10.190815
Iteration 600 / 1500: loss 7.100987
Iteration 700 / 1500: loss 5.926668
Iteration 800 / 1500: loss 5.126314
Iteration 900 / 1500: loss 5.678488
Iteration 1000 / 1500: loss 5.173691
Iteration 1100 / 1500: loss 5.729819
Iteration 1200 / 1500: loss 5.010818
Iteration 1300 / 1500: loss 5.567017
Iteration 1400 / 1500: loss 5.615139
输入任意关键字进行预测...
在交叉验证中实现的精度: 0.363400
KNN算法:精确度为0.24的精度没有svm精度高。
逻辑回归:
#! /usr/bin/python
# -*-coding: utf8 -*-
import matplotlib.pyplot as plt
import numpy as np
#逻辑回归就这个核心函数.
def sigmoid(z):
return 1.0/(1.0+np.exp(-z))
#通过plt进行划线
z = np.arange(-10,10,0.1)
p = sigmoid(z)
plt.plot(z,p)
#画一条竖直线,如果不设定x的值,则默认是0
plt.axvline(x=0, color='k')
plt.axhspan(0.0, 1.0,facecolor='0.7',alpha=0.4)
# 画一条水平线,如果不设定y的值,则默认是0
plt.axhline(y=1, ls='dotted', color='0.4')
plt.axhline(y=0, ls='dotted', color='0.4')
plt.axhline(y=0.5, ls='dotted', color='k')
plt.ylim(-0.1,1.1)
#确定y轴的坐标
plt.yticks([0.0, 0.5, 1.0])
plt.ylabel('$\phi (z)$')
plt.xlabel('z')
ax = plt.gca()
ax.grid(True)
plt.show()
通过dataset.txt数据集合。进行逻辑回归训练,逻辑回归算法:
~/work/cs231n$ python test_logRegression.py
Congratulations, training complete! Took 0.114466s!
The classify accuracy is: 93.000%