概率论复习笔记(一)随机事件及其概率
概率论复习笔记(一)随机事件及其概率
- 基本概念
- 随机试验
- 样本空间
- 随机事件
- 事件分类
- 事件及其运算关系
- 运算规律
- 频率与概率
- 概率的统计定义
- 概率的公理化定义
- 概率的性质
- 等可能概型( 古典概型 )
- 古典概型:
- 常用排列与组合的公式
- 几何概型
- 条件概率
- 定义
- 性质
- 乘法公式
- 全概率公式
- 贝叶斯公式:
- 独立性
- 两事件的独立性
- 三事件的独立性
- n n n个事件的独立性 :
- 典型例题
- 用事件之间的运算关系表示事件
- 事件概率的计算
- 利用概率的性质求概率
- 利用古典概型求概率
- 利用几何概型求概率
- 利用条件概率求概率
- 利用乘法定理求概率
- 利用全概率、贝叶斯公式求概率
- 利用事件的独立性求概率
- 本章小结
- 重点与难点
- 重点
- 难点
基本概念
随机试验
(1)试验可以在相同条件下重复进行;
(2)每次试验的可能结果不止一个,但能事先明确试验的所有可能结果;
(3)进行一 次试验之前 ,不能确定哪一个结果会出现 。
具有以上三个特征的试验叫做随机试验。 简称为试验,用记号 E 表示。
样本空间
把随机试验的所有基本事件组成的集合称为样本空间,常用 Ω \Omega Ω来记。其中基本事件也称为样本点。
随机事件
随机试验中的每一个可能结果称为随机事件(简称为事件),常用大写字母A,B,C等表示。
不可能再分的事件称为基本事件;而由基本事件复合而成的事件,称为复合事件 。
事件分类
基本事件: 不可能再分的事件。
复合事件:由基本事件复合而成的事件。
必然事件: 一定发生的事件,记作 Ω \Omega Ω。
不可能事件:一定不发生的事件,记作 ϕ \phi ϕ。
无 论 是 必 然 事 件 、随 机 事 件 还 是 不 可能 事 件 , 都 是 相 对 “ 一 定 条 件 ” 而 言 的 。条 件 发 生 变 化 , 事 件 的 性 质 也 发 生 变 化 。
事件及其运算关系
若记 Ω \Omega Ω:样本空间, ϕ \phi ϕ:不可能事件, e: 基本事件,A, B,… 为随机事件。则有事件之间的运算关系如下:
(1)包含关系:如果事件 A 发生必导致事件 B发生, 称事件 B 包含事件 A,记作A ⊂ \subset ⊂B
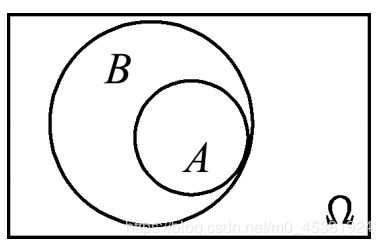
(2)相等关系:如果A ⊂ \subset ⊂B且B ⊂ \subset ⊂A,则称事件A 与B 相等,记作 A=B;
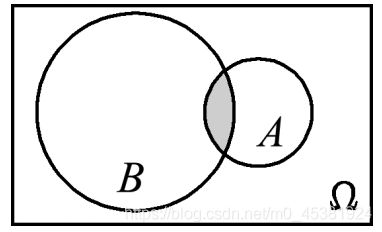
(3)和事件:事件A与B中,至少有—个发生,记作 A ∪ B A\cup B A∪B;
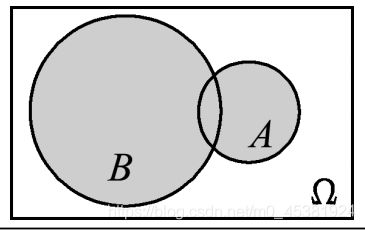
(4)积事件:事件 A、B同时发生,记作 A ∩ B A\cap B A∩B (简记为 A B AB AB);
(5)差事件: 事件 A与事件 B 的差事件,记作 A − B A-B A−B,表示 A发生而 B不发生;

(6)互不相容(互斥):若$ AB=\phi$,则称事件 A与事件 B互不相容;
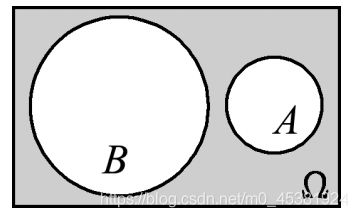
(7)对立事件(余事件): 事件B的对立事件记作 B ‾ \overline{B} B, 表示事件B不发生; 若$ AB=\phi且A\cup B$ ,则称事件 A与事件B互逆, 即 A ‾ = B , B ‾ = A \overline{A}=B,\overline{B}=A A=B,B=A。
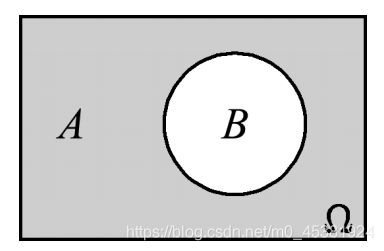
对立事件一定是互斥事件, 但互斥事件不一定是对立事件.
运算规律
(1)交换律: A ∪ B = B ∪ A ; A ∩ B = B ∩ A A\cup B=B\cup A;A\cap B=B\cap A A∪B=B∪A;A∩B=B∩A
(2)结合律: A ∪ ( B ∪ C ) = ( A ∪ B ) ∪ C ; A ∩ ( B ∩ C ) = ( A ∩ B ) ∩ C A\cup(B\cup C)=(A\cup B)\cup C;A\cap(B\cap C)=(A\cap B)\cap C A∪(B∪C)=(A∪B)∪C;A∩(B∩C)=(A∩B)∩C
(3)分配律: A ∪ ( B ∩ C ) = ( A ∪ B ) ∩ ( B ∪ C ) ; A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( B ∩ C ) A\cup(B\cap C)=(A\cup B)\cap(B\cup C);A\cap(B\cup C)=(A\cap B)\cup(B\cap C) A∪(B∩C)=(A∪B)∩(B∪C);A∩(B∪C)=(A∩B)∪(B∩C)
(4)德·摩根律: A ∪ B ‾ = A ‾ ∩ B ‾ ; A ∩ B ‾ = A ‾ ∪ B ‾ \overline{A\cup B}=\overline{A}\cap\overline{B};\overline{A\cap B}=\overline{A}\cup\overline{B} A∪B=A∩B;A∩B=A∪B
(5) 差积转换律: A − B = A B ‾ A-B=A\overline{B} A−B=AB
频率与概率
概率的统计定义
频率:在相同的条件下, 进行了 n 次试验, 在这 n 次试验中,事件 A发生的次数 n A n_A nA称为事件 A 发生的 频数 ,比值 n A n \frac {n_A}{n} nnA 称为事件 A发生的 频率 ,记作 f n ( A ) f_n(A) fn(A)
频率的一般性质:
- 0 ≤ f n ( A ) ≤ 1 0\leq f_n(A)\leq 1 0≤fn(A)≤1
- f n ( Ω ) = 1 f_n(\Omega)=1 fn(Ω)=1
- 可列可加性 : 设 A 1 , A 2 , ⋯ , A k A_1, A_2 ,\cdots , A_k A1,A2,⋯,Ak是两两互不相容的事件,有
f n ( A 1 ∪ A 2 ∪ ⋯ ∪ A k ) = f n ( A 1 ) + f n ( A 2 ) + ⋯ + f n ( A k ) f_n(A_1\cup A_2\cup \cdots\cup A_k)=f_n(A_1)+f_n(A_2)+\cdots+f_n(A_k) fn(A1∪A2∪⋯∪Ak)=fn(A1)+fn(A2)+⋯+fn(Ak)
概率的统计定义:在随机试验 E E E中, 当试验次数 n n n逐渐增大时, 频率值 f n ( A ) f_n(A) fn(A) 趋于稳定, 即在某个数 p p p附近波动,称数为事件 A 的概率, 即 P ( A ) = p P(A)=p P(A)=p。当 n 很大时, f n ( A ) ≈ p f_n(A)\approx p fn(A)≈p。人们总是用 n n n很大时 f n ( A ) f_n(A) fn(A) 作为 P ( A ) P(A) P(A) 的近似值, 即 P ( A ) ≈ f n ( A ) ( n 很 大 ) P(A)\approx f_n ( A ) ( n很大) P(A)≈fn(A)(n很大)。
概率的公理化定义
设$ \Omega 是 一 样 本 空 间 , 称 满 足 下 列 三 条 公 理 的 集 函 数 是一样本空间, 称满足下列三条公理的集函数 是一样本空间,称满足下列三条公理的集函数P(·) 为 定 义 在 为定义在 为定义在n$上的概率:
-
非负性:对任意事件 A, P ( A ) ≥ 0 P(A)\geq0 P(A)≥0;
-
规范性: P ( n ) = 1 P(n) = 1 P(n)=1;
-
可列可加性:若两两互不相容的事件列$ \lbrace A_n\rbrace$是可列的, 则
P ( ∑ i = 1 ∞ A i ) = ∑ i = 1 ∞ P ( A i ) P(\sum_{i=1}^\infty A_i)=\sum_{i=1}^\infty P(A_i) P(i=1∑∞Ai)=i=1∑∞P(Ai)
概率的性质
- P ( ∅ ) = 0. P(\emptyset) = 0. P(∅)=0.
- 有限可加性:若 n n n个事件 A 1 , A 2 , ⋯ , A n A_1, A_2 ,\cdots , A_n A1,A2,⋯,An两两互不相容, 则 P ( A 1 + A 2 + ⋯ + A n ) = P ( A 1 ) + P ( A 2 ) + ⋯ + P ( A n ) P(A_1+A_2+\cdots+A_n)=P(A_1)+P(A_2)+\cdots+P(A_n) P(A1+A2+⋯+An)=P(A1)+P(A2)+⋯+P(An)
- 相互对立两事件概率之和为 1, 即 P ( A ) + P ( A ‾ ) = 1. P(A)+ P(\overline{A}) = 1 . P(A)+P(A)=1.
- 若 A ⊂ B A\subset B A⊂B,则有 P ( B − A ) = P ( B ) − P ( A ) . P(B-A) = P(B)- P(A). P(B−A)=P(B)−P(A).
- 0 ≤ P ( A ) ≤ 1. 0\leq P(A)\leq1. 0≤P(A)≤1.
- P ( A ) = 1 − P ( A ) . P(A) = 1-P(A). P(A)=1−P(A).
- 加法公式:若A,B 是任意两个事件, 则$P( A\cup B ) = P( A ) + P( B ) - P( A B ). $
等可能概型( 古典概型 )
古典概型:
具有下列两个特点的试验称为古典概型试验。
- 每次试验只有有限种可能的试验结果;
- 每次试验中,每个基本事件出现的机会都是均等的;
对于古典概型试验, 事件 A 发生的概率为
P ( A ) = A 中 基 本 事 件 数 n 中 基 本 事 件 数 = m n P(A)=\frac {A中基本事件数}{n中基本事件数}=\frac {m}{n} P(A)=n中基本事件数A中基本事件数=nm
计算古典型概率 P(A) 的关键是找出 A 中的基本事件数, 在计算过程中常常用到排列组合的知识, 有时也需要用列举法逐一分析 A 中的基本事件.
不放回抽样: 第一次抽取后, 不放回, 第二次从剩余的样本中抽取 。
放回抽样: 第一次抽取后, 观察后放回, 搅匀后再抽取.则第二次抽取前的情况和第一次抽取前的情况相同 。
常用排列与组合的公式
不重复排列公式: 从 n n n个不同元素中任取 m m m个不同元素按照一定的顺序排成一列, 其排列数为
P n m = n ! ( n − m ) ! P_{n}^m= \frac{n!}{(n-m)!} Pnm=(n−m)!n!
可重复排列公式: 从 n n n个不同元素中有放回地抽取 m m m个元素, 按照一定顺序排成一列, 其排列总数为 N = n m N=n^m N=nm
组合公式: 从 " 个不同元素中每次取出个不同元素, 不考虑顺序组成一组, 其组合总数为
C n m = 1 m ! P n m = n ! m ! ( n − m ) ! C_n^m=\frac 1 {m!}P_n^m=\frac {n!}{m!(n-m)!} Cnm=m!1Pnm=m!(n−m)!n!
组合性质 :
C n m = C n n − m ; C n m = C n − 1 m + C n − 1 m − 1 ; ∑ r = 0 m C n 1 r C n 2 m − r = C n 1 + n 2 m ; ∑ m = 0 m C n m = 2 n C_n^m=C_n^{n-m};C_n^m=C_{n-1}^m+C_{n-1}^{m-1};\sum_{r=0}^{m}C_{n_1}^{r}C_{n_2}^{m-r}=C_{n_1+n_2}^{m};\sum_{m=0}^{m}C_n^m=2^n Cnm=Cnn−m;Cnm=Cn−1m+Cn−1m−1;r=0∑mCn1rCn2m−r=Cn1+n2m;m=0∑mCnm=2n
加法原理: 如果完成一件工作有 m m m个不同方法, 其中任何一个方法都可一次完成这件工作。假设第 i i i个方法有 n i n_i ni个方案, i = 1 , 2 , ⋯ , m , i=1,2,\cdots,m, i=1,2,⋯,m, 则完成该工作的全部方案有 n 1 + n 2 + ⋯ + n m n_1+n_2+\cdots+n_m n1+n2+⋯+nm个 。
乘法原理: 如果一件工作需先后经 m m m个不同步骤才能最后完成, 其中第 i i i个步骤有 n i n_i ni个不同方案, i = 1 , ⋯ , m , i=1,\cdots,m, i=1,⋯,m,则完成该件工作共有 n 1 n 2 ⋯ n m n_1n_2\cdots n_m n1n2⋯nm种不同方案。
几何概型
几何概型 : 如果随机试验的样本空间是一个区域(例如直线上的区间、平面或空间中的区域) , 而且样本空间中每个试验结果的出现具有等可能性,那么事件 A 的概率为
P ( A ) = A 的 测 度 ( 长 度 、 面 积 、 体 积 ) 样 本 空 间 的 测 度 ( 长 度 、 面 积 、 体 积 V ) P(A)=\frac {A 的测度(长度、 面积、体积)}{样本空间的测度(长度、 面积、体积V)} P(A)=样本空间的测度(长度、面积、体积V)A的测度(长度、面积、体积)
几何概率的计算中往往需要利用定积分及重积分求面积或体积
条件概率
定义
条件概率 :设两事件 A , B A,B A,B 且$ P(A)> 0,$则称
P ( B ∣ A ) = P ( A B ) P ( A ) P(B\mid A)=\frac {P(AB)}{P(A)} P(B∣A)=P(A)P(AB)
为事件 A 发生的条件下, 事件 B 发生的条件概率 。
性质
条件概率与概率有相同的性质 :
-
对任意事件B, 0 ≤ P ( B ∣ A ) ≤ 1 0\leq P(B\mid A)\leq 1 0≤P(B∣A)≤1
-
P ( Ω ∣ A ) = 1 P(\Omega\mid A)=1 P(Ω∣A)=1
-
若 B 1 , B 2 , ⋯ B_1,B_2,\cdots B1,B2,⋯是两两互斥事件,则有
P ( ⋃ i = 1 ∞ B i ∣ A ) = ∑ i = 1 ∞ P ( B i ∣ A ) P(\bigcup_{i=1}^\infty B_i\mid A)=\sum_{i=1}^\infty P(B_i\mid A) P(i=1⋃∞Bi∣A)=i=1∑∞P(Bi∣A) -
对任意两事件 B 1 , B 2 , B_1,B_2, B1,B2,有 P ( B 1 ∪ B 2 ∣ A ) = P ( B 1 ∣ A ) + P ( B 2 ∣ A ) − P ( B 1 B 2 ∣ A ) . P(B_1\cup B_2\mid A)=P(B_1\mid A)+P(B_2\mid A)-P(B_1B_2\mid A). P(B1∪B2∣A)=P(B1∣A)+P(B2∣A)−P(B1B2∣A).
① 条件概率与一般概率的区别.
条件概率是指在事件 A 发生的条件下事件 B 发生的概率.条件概率是以 A 这样一个新的样本空间来考虑问题的 ;
一般概率是以基本事件的总数构成的样本空间来考虑的.
② 注 意 条 件 概 率 和 乘 法 之 间 的 区 别.
P(BA)表示 A 发生并且 B 发生的概率;
P(B|A) 表示在A 发生的条件下 B 发生的概率.
乘法公式
P ( A B ) = { P ( A ) P ( B ∣ A ) , 当 P ( A ) > 0 P ( B ) P ( A ∣ B ) , 当 P ( B ) > 0 P(AB)= \begin{cases} P(A)P(B\mid A), & \text{当$P(A)>0$} \\ P(B)P(A\mid B), & \text{当$P(B)>0$} \end{cases} P(AB)={P(A)P(B∣A),P(B)P(A∣B),当P(A)>0当P(B)>0
全概率公式
划分:设 Ω \Omega Ω为试验E的样本空间 , B 1 , B 2 , ⋯ , B n ,B_1,B_2,\cdots,B_n ,B1,B2,⋯,Bn为 E E E的一组事件.若
- B i B j = ∅ , i ≠ j , i , j = 1 , 2 , ⋯ , n ; B_iB_j=\emptyset,i\neq j,i,j=1,2,\cdots,n; BiBj=∅,i=j,i,j=1,2,⋯,n;
- B 1 ∪ B 2 ∪ ⋯ ∪ B n = Ω B_1\cup B_2\cup\cdots\cup B_n=\Omega B1∪B2∪⋯∪Bn=Ω
则称 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn为样本空间 Ω \Omega Ω的一个划分, 也称为完备事件组.
若 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn是样本空间的一个划分, 那么,对每次试验, 事件 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn中必有一个且仅有一个发生.
全概率公式:
设试验 E E E的样本空间为 Ω \Omega Ω,A 为 E E E的事件 , B 1 , B 2 , ⋯ , B n ,B_1,B_2,\cdots,B_n ,B1,B2,⋯,Bn为 S 的一个划分, 且 P ( B i ) > 0 ( i = 1 , 2 , ⋯ , n ) , P(B_i)> 0(i= 1,2,\cdots,n), P(Bi)>0(i=1,2,⋯,n),则
P ( A ) = P ( A ∣ B 1 ) P ( B 1 ) + P ( A ∣ B 2 ) P ( B 2 ) + ⋯ + P ( A ∣ B n ) P ( B n ) P(A)=P(A\mid B_1)P(B_1)+P(A\mid B_2)P(B_2)+\cdots+P(A\mid B_n)P(B_n) P(A)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+⋯+P(A∣Bn)P(Bn)称为全概率公式。
贝叶斯公式:
设试验 E E E的样本空间为 Ω \Omega Ω。A为 E E E 的事件为 S , B 1 , B 2 , ⋯ , B n ,B_1,B_2,\cdots,B_n ,B1,B2,⋯,Bn 的一个划分, 且 P ( A ) > 0 , P ( B i ) > 0 ( i = 1 , 2 , ⋯ , n ) , P(A)>0,P(B_i)> 0(i= 1,2,\cdots,n), P(A)>0,P(Bi)>0(i=1,2,⋯,n),
P ( B i ∣ A ) = P ( A ∣ B i ) P ( B i ) ∑ j = 1 n P ( A ∣ B j ) P ( B j ) , i = 1 , 2 , ⋯ , n . P(B_i\mid A)=\frac {P(A\mid B_i)P(B_i)}{\sum_{j=1}^{n}P(A\mid B_j)P(B_j)},i=1,2,\cdots,n. P(Bi∣A)=∑j=1nP(A∣Bj)P(Bj)P(A∣Bi)P(Bi),i=1,2,⋯,n.
则称为贝叶斯(Bayes)公式 。
独立性
两事件的独立性
设 A,B 是两事件, 如果满足等式 P ( A B ) = P ( A ) P ( B ) , P(AB ) = P(A)P(B), P(AB)=P(A)P(B),则称事件 A,B 相互独立, 简称 A,B 独立。
容易知道, 若$P(A)>0,P(B)>0, $则A,B相互独立与 A,B 互不相容不能同时成立.
定理一:设 A,B是两事件, 且$ P(A)> 0. 若 A , B 相 互 独 立 , 则 若 A,B相互独立, 则 若A,B相互独立,则 P( B|A) = P(B).$反之亦然.
定理二:若事件 A,B 相互独立,则下列事件也相互独立, A A A与 B ‾ \overline{B} B, B B B与 A ‾ \overline{A} A, A ‾ \overline{A} A,与 B ‾ \overline{B} B,
A 与 B 独 立 ⇔ P ( A ∣ B ) = P ( A ∣ B ‾ ) = P ( A ) ( 0 < P ( B ) < 1 ) . ⇔ P ( B ∣ A ) = P ( B ‾ ∣ A ) = P ( B ) ( 0 < P ( A ) < 1 ) . A 与B 独立\\ \Leftrightarrow P(A\mid B)=P(A\mid \overline{B})=P(A)(0
三事件的独立性
两两独立:设 A , B , C A,B,C A,B,C 是三事件, 如果
{ P ( A B ) = P ( A ) P ( B ) , P ( B C ) = P ( B ) P ( C ) , P ( A C ) = P ( A ) P ( B ) , \begin{cases} P(AB)=P(A)P(B),\\ P(BC)=P(B)P(C),\\ P(AC)=P(A)P(B), \end{cases} ⎩⎪⎨⎪⎧P(AB)=P(A)P(B),P(BC)=P(B)P(C),P(AC)=P(A)P(B),
则称三事件两两独立。
相互独立:设 A , B , C A,B,C A,B,C 是三事件, 如果
{ P ( A B ) = P ( A ) P ( B ) , P ( B C ) = P ( B ) P ( C ) , P ( A C ) = P ( A ) P ( B ) , P ( A B C ) = P ( A ) P ( B ) P ( C ) \begin{cases} P(AB)=P(A)P(B),\\ P(BC)=P(B)P(C),\\ P(AC)=P(A)P(B),\\ P(ABC)=P(A)P(B)P(C) \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧P(AB)=P(A)P(B),P(BC)=P(B)P(C),P(AC)=P(A)P(B),P(ABC)=P(A)P(B)P(C)
则称 A,B,C 为相互独立的事件。
当事件 A,B,C 两两独立时, 等式 P( ABC ) =P(A)P(B)P© 不一定成立.
A,B,C 两两独立是 A,B,C 相互独立的必要条件但不是充分条件.
n n n个事件的独立性 :
一般,设 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An是 n ( n ≥ 2 ) n(n\geq2) n(n≥2)个事件, 如果对于其中任意 2 个, 任意 3 个,…, 任意 n 个事件的积事件的概率, 都等于各事件概率之积,则称事件 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An相互独立.
推论:
(1) 若 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An相互独立, 则它们中的任何一部分事件也相互独立;
(2) 若 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An相互独立,则它们中的任何一部分事件换成各自的对立事件后所得到 n n n个事件仍是相互独立的;
(3)若 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An相互独立,则
P ( A 1 A 2 ⋯ A n ) = ∏ i = 1 n P ( A i ) , ⋃ i = 1 n P ( A i ‾ ) = 1 − ∏ i = 1 n P ( A i ‾ ) . P(A_1A_2\cdots A_n)=\prod_{i=1}^{n}P(A_i),\bigcup_{i=1}^{n}P(\overline{A_i})=1-\prod_{i=1}^{n}P(\overline{A_i}). P(A1A2⋯An)=i=1∏nP(Ai),i=1⋃nP(Ai)=1−i=1∏nP(Ai).
典型例题
用事件之间的运算关系表示事件
事件概率的计算
利用概率的性质求概率
利用古典概型求概率
利用几何概型求概率
利用条件概率求概率
小明概率论考试得80分以上的概率是80%,得60分以上的概率是85%,已知这次考试小明概率论没挂,那么小明得80分以上的概率是多少?
事件A:小明得60分以上
事件B:小明得80分以上
P(B|A):小明得60分以上时,小明得80分以上的概率
P(AB):小明得80分以上的概率
P ( B ∣ A ) = P ( A B ) P ( A ) = 80 % 85 % = 16 17 P(B\mid A)=\frac {P(AB)}{P(A)}=\frac {80\%}{85\%}=\frac {16}{17} P(B∣A)=P(A)P(AB)=85%80%=1716
利用乘法定理求概率
利用全概率、贝叶斯公式求概率
某公司有小明与小红两个员工,老板要抽其中一个考核,抽中小明与小红的概率都是50%,小明考核通过的概率是100%,小红考核通过的概率是1%,求抽中的员工通过考核时,被抽中的员工是小红的概率。
设抽中的员工为小明,小红分别为事件 B 1 , B 2 B_1,B_2 B1,B2
P ( A ) = P ( B 1 ) P ( A ∣ B 1 ) + P ( B 2 ) P ( A ∣ B 2 ) = 50 % × 100 % + 50 % × 1 % = 50.5 % P(A)=P(B_1) P(A\mid B_1)+P(B_2) P(A\mid B_2)=50%×100%+50%×1%=50.5% P(A)=P(B1)P(A∣B1)+P(B2)P(A∣B2)=50%×100%+50%×1%=50.5%
P ( B 2 ∣ A ) = P ( A ∣ B 2 ) P ( B 2 ) P ( A ) = 50 % ∗ 1 % 50.5 % = 1 101 P(B_2\mid A)=\frac{P(A\mid B_2)P(B_2)}{P(A)}\\ =\frac{50\%*1\%}{50.5\%}\\ =\frac{1}{101} P(B2∣A)=P(A)P(A∣B2)P(B2)=50.5%50%∗1%=1011
利用事件的独立性求概率
本章小结
六个概念:随机试验、随机事件、样本空间、频率、概率、事件的独立性;
三个公式:条件概率及乘法公式、全概率公式和贝叶斯公式;
两个概型:古典概型、几何概型。
重点与难点
重点
- 随机事件及事件间的运算关系。
- 概率的公理化定义及概率的基本性质的应用。
- 乘法定理及条件概率公式。
- 事件的独立性及其应用。
难点
- 概率的公理化定义及概率的基本性质的应用。
- 古典概率的计算及条件概率、全概率公式和贝叶斯(bayes)公式的应用。