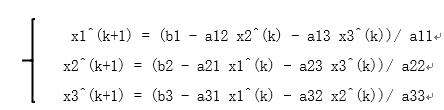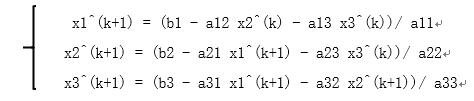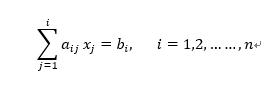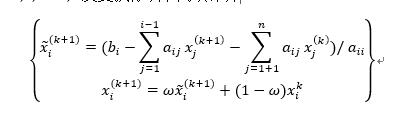求解线性方程组： 高斯消元--LU分解--Jacobi迭代--高斯赛德尔--sor超松弛迭代
求解线性方程组： 高斯消元--LU分解--Jacobi迭代--高斯赛德尔--sor超松弛迭代
1.问题概述
假定线性方程组
是一个最基本的计算模型，它在科学与工程计算中扮演着极其重要的角色。
在解决此线性方程组时，我们首先想到的是线性代数课程中的求解方法，然而对于计算机来说，这是很难实现的，所以我们应当对此方法进行变形拓展。随着未知数个数的增加，求解就会变得越来越困难，当n很大时，用手工计算已经不可能，只能借助计算机了，而计算机只能表示有限精度的数，计算过程必然出现误差，这样一来，如何快速有效的利用计算机来求解大型线性方程组就成为科学与工程计算领域的核心问题（快速有效）。
1.直接法
求解线性方程组的直接法，就是通过有限步的运算手续，将所给方程组直接加工成某个三角方程组乃至对角方程组来求解。
求解线性方程组的直接法主要分为消去法与矩阵分解方法两大类。2.迭代法
求解大规模的线性方程组主要用迭代法。迭代法的设计思想是将“复杂”化归为“简单”的重复，即：将所给线性方程组的求解
过程化归为三角方程组或对角方程组求解过程的重复。
1.高斯消元法（Gaussian Elimiination）
原理：将第一行以下的等式中的x1消除，然后再将第二行以下的等式中的x2消除......这样可使整个方程组变成一个三角形似的格式，产生出一个“行梯阵式”。然后由后向前便可依次求出每一个未知数x的值。
这种算法可以用来解决所有线性方程组。即使一个方程组不能被化为一个三角形的格式，高斯消元法仍可找出它的解。
for (int k = 0; k < 5; k++)
{
for (int i = k + 1; i < 6; i++)
{
temp = third.ele[i][k] / third.ele[k][k];
for (int j = k; j < 6; j++)
{
third.ele[i][j] -= temp*third.ele[k][j];
}
b3[i] -= temp*b3[k];
}
}
for (int i = 5; i >= 0; i--)
{
x[i] = b3[i];
for (int j = 5; j >= 0; j--)
{
if (i != j)
{
x[i] -= third.ele[i][j] * x[j];
}
}
x[i] /= third.ele[i][i];
}
2.LU分解(LU decomposition)
事实上，设将系数矩阵A分解成下三角矩阵L与上三角矩阵U的乘积
A=LU
则所给方程组Ax=b即
L(Ux)=b
可化为两个三角方程组
Ly=b,Ux=y
来求解，三角方程组有简单的回带公式，求解是方便的。
这里，下三角方程组Ly=b的回代过程是顺序计算y1→y2→…→yn的追的过程，而上三角方程组Ux=y的回代过程则是逆序求解xn→xn-1→…→x1的赶的过程，因此，上述矩阵分解方法可理解为广义的追赶法。
为了保证分解式A=LU的唯一性，实际的附加条件是，令其中一个分解阵L或U的对角线元素全为1.
3.Jacobi迭代
Jacobi迭代的设计思想是将所给线性方程组逐步对角化.
首先考察三阶方程组的具体情形
令其左端保留对角成分，将其余成分挪到右端，而改写成如下“伪对角形式”：
用预报值x1^(k), x2^(k), x3^(k)代替上式右端，求得的解x1^(k+1), x2^(k+1),x3^(k+1)称作校正值，这样建立的预报校正系统为：
相应的迭代公式为：
进而考察一般形式的方程组(2),依据这种等价形式可建立Jacobi迭代
xi^(k+1) = (bi -∑aij xj^(k))/ aii , i=1,2,…,n (j=1-n,j≠i)
do
{
if ((++cnt) > cnt) break;
for (int i = 0; i < 6; i++) x1[i] = x[i];
for (int i = 0; i < 6; i++)
{
temp = 0;
for (int j = 0; j < 6; j++)
{
if (i != j)
{
temp += third.ele[i][j] * x1[j];
}
}
x[i] = (b3[i] - temp) / third.ele[i][i];
// cout << x[i] << endl;
}
// cout << endl;
ep = 0;
for (int i = 0; i < 6; i++)
{
if (ep < (abs(x[i] - x1[i])))
{
ep = abs(x[i] - x1[i]);
}
}
} while (ep > e);
4.高斯赛德尔
（
gauss_seidel（）
xk+1=xk + e^-1 * rk
Jacobi迭代的设计思想是将所给线性方程组逐步对角化.令其左端保留对角成分，将其余成分挪到右端，而改写成如下“伪对角形式”：
与Jacobi相似，不过在根据已知点求解时（已知点改变），建立的预报校正系统为：
相应的迭代公式为：
进而考察一般形式的方程组(2),依据这种等价形式可建立Jacobi迭代
xi^(k+1) = (bi -∑aij xj^(k))/ aii , i=1,2,…,n (j=1-n,j≠i)
do
{
if ((++cnt) > 100) break;
for (int i = 0; i < 6; i++) x1[i] = x[i];
for (int i = 0; i < 6; i++)
{
temp = 0;
for (int j = 0; j < 6; j++)
{
if (i != j)
{
if (j < i)
{
temp += third.ele[i][j] * x[j];
}
else temp += third.ele[i][j] * x1[j];
}
}
x[i] = (b3[i] - temp) / third.ele[i][i];
// cout << x[i] << endl;
}
// cout << endl;
ep = 0;
for (int i = 0; i < 6; i++)
{
if (ep < (abs(x[i] - x1[i])))
{
ep = abs(x[i] - x1[i]);
}
}
} while (ep > e);
5.sor超松弛迭代
使用迭代法的困难所在是计算量难以估计。有时迭代过程虽然收敛，但收敛速度缓慢，使计算量变得很大而失去实用价值。因此，迭代过程的加速具有重要意义。所谓迭代加速，就是运用松弛技术，将Gauss-Seidel迭代值进一步加工成某种松弛值，以尽量改善精度。
对于一般的方程组
其松弛迭代对 i=1,2,...,n 反复执行以下两项计算。
要求取松弛因子 w>1 ,以尽量发挥新值的优势。
do
{
if ((++cnt) > 100) break;
for (int i = 0; i < 6; i++) x1[i] = x[i];
for (int i = 0; i < 6; i++)
{
temp = 0;
for (int j = 0; j < 6; j++)
{
if (i != j)
{
if (j < i)
{
temp += third.ele[i][j] * x[j];
}
else temp += third.ele[i][j] * x1[j];
}
}
x[i] = (1 - w)*x[i] + w*(b3[i] - temp) / third.ele[i][i];
// cout << x[i] << endl;
}
// cout << endl;
ep = 0;
for (int i = 0; i < 6; i++)
{
if (ep < (abs(x[i] - x1[i])))
{
ep = abs(x[i] - x1[i]);
}
}
} while (ep > e);
注意：先将方程化为
主对角占优
End