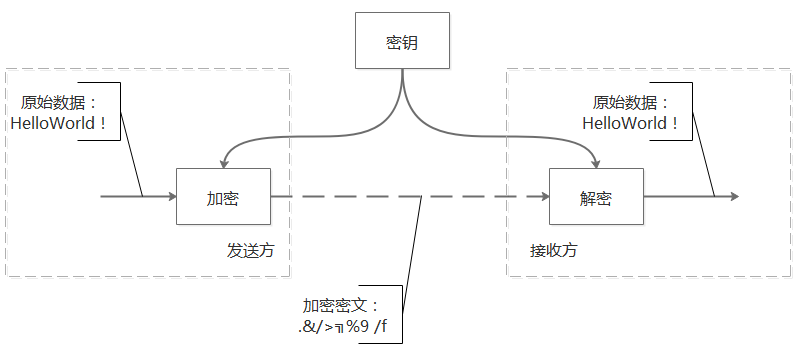
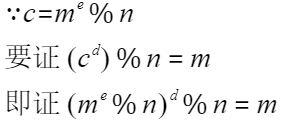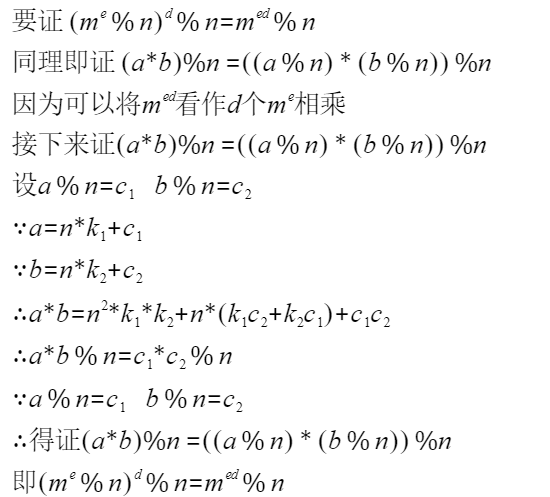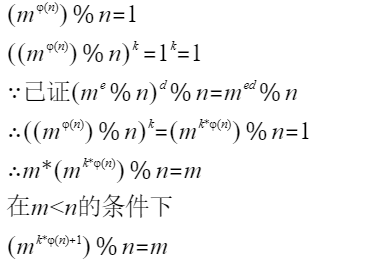- ARM驱动学习之4小结
JT灬新一
嵌入式C++arm开发学习linux
ARM驱动学习之4小结#include#include#include#include#include#defineDEVICE_NAME"hello_ctl123"MODULE_LICENSE("DualBSD/GPL");MODULE_AUTHOR("TOPEET");staticlonghello_ioctl(structfile*file,unsignedintcmd,unsignedlo
- react-intl——react国际化使用方案
苹果酱0567
面试题汇总与解析java开发语言中间件springboot后端
国际化介绍i18n:internationalization国家化简称,首字母+首尾字母间隔的字母个数+尾字母,类似的还有k8s(Kubernetes)React-intl是React中最受欢迎的库。使用步骤安装#usenpmnpminstallreact-intl-D#useyarn项目入口文件配置//index.tsximportReactfrom"react";importReactDOMf
- Linux CTF逆向入门
蚁景网络安全
linux运维CTF
1.ELF格式我们先来看看ELF文件头,如果想详细了解,可以查看ELF的manpage文档。关于ELF更详细的说明:e_shoff:节头表的文件偏移量(字节)。如果文件没有节头表,则此成员值为零。sh_offset:表示了该section(节)离开文件头部位置的距离+-------------------+|ELFheader|---++--------->+-------------------
- Windows安装ciphey编码工具,附一道ciscn编码题例
im-Miclelson
CTF工具网络安全
TA是什么一款智能化的编码分析解码工具,对于CTF中复杂性编码类题目可以快速攻破。编码自动分析解码的神器。如何安装Windows环境Python3.864位(最新的版本不兼容,32位的也不行)PIP直接安装pipinstallciphey-ihttps://pypi.mirrors.ustc.edu.cn/simple/安装后若是出现报错请根据错误代码行数找到对应文件,r修改成rb即可。使用标准语
- 2005年高考英语北京卷 - 阅读理解C
让文字更美
Howcouldwepossiblythinkthatkeepinganimalsincagesinunnaturalenvironments-mostlyforentertainmentpurposes-isfairandrespectful?我们怎么可能认为把动物关在非自然环境的笼子里——主要是为了娱乐目的——是公平和尊重的呢?Zooofficialssaytheyareconcernedab
- CTF-bugku-crypto-[7+1+0]-base64解码之后做偏移
沧海一粟日尽其用
算法安全python
CTF-bugku-crypto-[7+1+0]-base64解码之后做偏移1.题目2.解题思路2.1base64编码原理2.2解题思路2.2.1base64解码找规律2.2.2破解思路3.解题脚本4.flag5.附EASCII码表1.题目提示信息:7+1+0?格式bugku{xxxxx}密文:4nXna/V7t2LpdLI44mn0fQ==要求:破解密文获得flag2.解题思路2.1base64
- CTF常见编码及加解密(超全)第二篇
不会代码的小徐
编码密码网络安全密码学预编码
HTML实体编码简述:字符实体是用一个编号写入HTML代码中来代替一个字符,在使用浏览器访问网页时会将这个编号解析还原为字符以供阅读。举例:highlighter-HTML明文:hello,world.十进制:hello,world.十六进制:hel
- CTF——web方向学习攻略
一则孤庸
CTF网络安全CTF
1计算机基础操作系统:熟悉Linux命令,方便使用Kali。网络技术:HCNA、CCNA。编程能力:拔高项,有更好。2web应用HTTP协议:必须掌握web开发框架web安全测试3数据库数据库基本操作SQL语句数据库优化4刷题
- CTF——web总结
oliveira-time
ctfweb安全
解题思路做题先看源码关注可下载的资源(zip压缩包)抓包寻找可能存在的加密信息(base64)不管三七二十一先扫描目录再说ps:正常的应该是先扫描目录,然后发现后台进行爆破,发现爆破困难,然后去社工找其他信息。CTF——web个人总结_ctfweb-CSDN博客
- VueTreeselect el-tree-select 多选
小小并不小
Vueelementjsvue.jsjavascript
1、VueTreeselect是一个多选组件npminstall--save@riophae/vue-treeselect全部代码//importthecomponentimportTreeselectfrom'@riophae/vue-treeselect'//importthestylesimport'@riophae/vue-treeselect/dist/vue-treeselect.cs
- ctf逆向解题——Bomb二进制炸弹
Funkypantss
BombPhase1在输入阶段将由文件输入的字符存储在input中,在phase1,该阶段将原字符串存储到rdi中,调用pases_1函数进行字符串比较。image进入phase1函数,该函数将原字符串rdi与预先设定的字符串“BorderrelationswithCanadahaveneverbeenbetter.”(存储在rsi中)进行比较,用于比较的函数是strings_not_equal,
- 【CTF】MISC常用工具集锦/使用方法简介
不会代码的小徐
misc网络安全测试工具
前言#MISC题型多变而且工具繁杂,因此自己花时间整理了一份工具列表,以便日后参考用流畅地阅读这篇博客,你可能需要:Python2.7.18+Python3.8+任何一个更高版本的Python,使用conda管理Linux虚拟机,kali即可流畅访问Google/GitHub等站点的网络通用工具#PuzzleSolver#专为misc手打造的瑞士军刀(?),整合了多种脚本(base,字频分析,pn
- 网络安全的相关比赛有哪些?需要掌握哪些必备技能?
网安学习
web安全安全网络安全的相关比赛有哪
01、CTF(夺旗赛)这是一种最常见的网络安全竞技形式,要求参赛者在限定时间内解决一系列涉及密码学、逆向工程、漏洞利用、取证分析等领域的挑战,获取标志(flag)并提交得分。通过举办CTF来培养网络安全人才,已经发展成为了国际网络安全圈的共识。CTF赛事可以分为线上赛和线下赛,线上赛通常是解题模式(Jeopardy),线下赛通常是攻防模式(Attack-Defense)。CTF赛事的代表性线下赛事
- 第四部分:1---文件内核对象,文件描述符,输出重定向
S+叮当猫
LinuxCentOS算法linux服务器
目录structfile内核对象:如何读写文件?文件描述符在文件描述符表中的分配规则:输出重定向初步解析:dup2实现复制文件描述符:structfile内核对象:structfile是在内核空间中创建的用于描述文件的结构体,每当一个文件被打开时,内核会为该文件创建一个对应的structfile结构体,并在文件描述符表中为其分配一个文件描述符。基于文件的定义(文件=内容+属性),structfil
- 网络攻防WEB入门指南
youhao108
网络攻防web渗透测试网络安全网络攻防
网络攻防WEB入门指南(大佬绕路)文章目录前言学习网络攻防该如何入门前言我对网络攻防的理解,分为比赛和实战两个部分,两者所学习的知识虽有共通之处,但还是有很大区别,我也在向实战的状态转换,不过二者入门所要掌握的知识差别不大。下面主要从网络攻防竞赛角度,也就是知名的CTF夺旗赛,来谈谈网络攻防知识如何入门。学习网络攻防该如何入门常规CTF比赛主要分为线上做题,以及线下AWD攻防(AttackWith
- 软考 - 系统架构设计师 - 设计模式
小林想被监督学习
系统架构设计师系统架构设计模式
目录概念创建型设计模式抽象工厂模式(AbstractFactoryPattern)优点缺点应用场景总结构建器模式(BuilderPattern)优点缺点应用场景工厂方法模式(factorymethod)优点缺点应用场景原型模式(prototype)优点缺点应用场景单例模式(Singleton)优点缺点应用场景结构型设计模式适配器模式(Adapter)优点缺点应用场景桥接模式(Bridge)优点缺点
- ctfshow web入门 ssrf web351~web360
kikkeve
ctfshowphpweb安全安全
目录SSRF基础web351web352、353web354web355web356web357web358web359web360SSRF基础SSRF(Server-SideRequestForgery:服务器端请求伪造)就是让服务器去请求服务器的资源,因为我们远程请求不到。curl_init():初始curl会话curl_setopt():会话设置curl_exec():执行curl会话,获取
- flutter 一键打出不同包名、应用名、版本名、签名、应用图标、版本号的安装包
Sindyue
flutter
1.build.gradle文件中配置不同的应用信息flavorDimensions"app"productFlavors{app1{//配置包名manifestPlaceholders=[str:"releaseStr",package_name:"com.example.demo1"]applicationId"com.example.demo1"versionCode1versionName
- CTF 竞赛密码学方向学习路径规划
David Max
CTF学习笔记密码学ctf信息安全
目录计算机科学基础计算机科学概念的引入、兴趣的引导开发环境的配置与常用工具的安装WattToolkit(Steam++)、机场代理Scoop(Windows用户可选)常用Python库SageMathLinux小工具yafuOpenSSLMarkdown编程基础Python其他编程语言、算法与数据结构(可选)数学基础离散数学与抽象代数复杂性分析密码学的正式学习兴趣的培养做题小技巧系统学习需要了解并
- MySQL8.0新特性~最左前缀匹配原则被打破了
进击的CJR
mysqlmysql
测试在MySQL8.0.25和mysql5.7.33中创建如下CREATETABLEt1(f1INTNOTNULL,f2INTNOTNULL,PRIMARYKEY(f1,f2));INSERTINTOt1VALUES(1,1),(1,2),(1,3),(1,4),(1,5),(2,1),(2,2),(2,3),(2,4),(2,5);INSERTINTOt1SELECTf1,f2+5FROMt1;
- hackcon ctf 2018 | pwn wp
fantasy_learner
BOF漏洞点:栈溢出利用过程栈溢出跳转callMeMaybe函数获得flagexpSheSellsSeaShells90流程分析:给出了输入的栈地址有一个栈溢出点没有nx利用过程:根据以上三点,得出可以使用ret2shellcode使用shellcraft生成shellcode利用栈溢出,输入并跳转到shellcodeexpSimpleYetElegent150这道题目做了最久,卡在了能否根据_d
- BUUCTF 2021-10-4 Pwn
Ch1lkat
BUUCTFPwnlinuxpwn
文章目录保持手感echo分析EXPPwnme1分析EXPwdb_2018_1st_babyheap分析EXPFSOPhouseoforange_hitcon_2016分析前置知识House_of_orangeFSOPEXPzctf_2016_note3分析EXPgyctf_2020_document分析EXP动态调试复现护网杯_gettingstart分析EXPpicoctf_2018_buffe
- C# 关于多线程同步不同实现方式
語衣
C#知识补充c#开发语言
栏目总目录AutoResetEventclassMainClass{//thearrayofconsumerthreadsprivatestaticListconsumers=newList();//thetaskqueueprivatestaticQueuetasks=newQueue();//thesynchronisationobjectforlockingthetaskqueuepriva
- Android里的设计模式
jim_dayday_up
#Android_基础知识设计模式java开发语言
一:设计模式分类经典的23种设计模式是由ErichGamma、RichardHelm、RalphJohnson和JohnVlissides(合称“GangofFour”)在他们的书《设计模式:可复用面向对象软件的基础》中定义的。以下是这些设计模式的分类和简要介绍。1.1创建型模式单例模式(Singleton):确保一个类只有一个实例,并提供一个全局访问点。抽象工厂模式(AbstractFactor
- 软考——简单记忆设计模式
Yeira
设计模式pythonjava
抽象工厂模式(AbstractFactory):提供一个接口,可以创建一系列相关或相互依赖的对象,而无需指定它们具体的类。(一个接口创建相关对象,无需具体的类)构建器模式(Builder):将一个复杂类的表示与其构造相分离,使得相同的构建过程能够得出不同的表示。(相同是构造,不同的表示)工厂方法模式(FactoryMethod):定义一个创建对象的接口,但由子类决定需要实例化哪一个类。工厂方法使得
- 【软考】设计模式之抽象工厂模式
王佑辉
软考设计模式软考
目录1.说明2.应用场景3.结构图4.构成5.适用性6.优点7.缺点8.java示例1.说明1.提供一个创建一系列相关或相互依赖对象的接口,而无须指定它们具体的类。2.抽象工厂模式(AbstractFactoryPattern)是一种创建型设计模式。3.抽象工厂模式用于系统的产品族,而不仅仅是一个等级结构;一个等级的抽象类只能创建一个等级的产品,而抽象工厂模式能创建多个等级的产品。2.应用场景1.
- 30、基于SelectFromModel和LassoCV的特征选择
凌晨思索
30、基于SelectFromModel和LassoCV的特征选择importmatplotlib.pyplotaspltimportnumpyasnpfromsklearn.datasetsimportload_diabetesfromsklearn.feature_selectionimportSelectFromModelfromsklearn.linear_modelimportLasso
- 【鸿蒙HarmonyOS开发笔记】使用@Preview装饰器预览组件
Luxine.
鸿蒙HarmonyOS开发笔记前端分享笔记华为harmonyos
概述ArkTS应用/服务支持组件预览,要求compileSdkVersion为8或以上。组件预览支持实时预览,不支持动态图和动态预览。组件预览通过在组件前添加注解@Preview实现,在单个源文件中,最多可以使用10个@Preview装饰自定义组件。@Preview的使用参考如下示例@Preview({title:'FoodImage'})@ComponentstructFoodImageDisp
- vue3+tesseract 图片文字提取
妙明元心
javascriptvue.jsecmascript
github:https://github.com/naptha/tesseract.js可实现多语言识别,中英文混合识别demo如下:importTesseractfrom"tesseract.js"//方式1:Tesseract.recognize('http://localhost:5173/vue.jpg','eng+chi_sim',).then((d)=>{console.log(d.
- iOS M1芯片Mac上Xcode模拟器报错解决
aven_kang
真机编译可以通过,模拟器失败,出现以下错误...,buildingforiOSSimulator,butlinkinginobjectfilebuiltforiOS,file'...'或者couldnotfindmodulefortarget'x86_64-apple-ios-simulator'解决方案一1.添加arm64到项目PEROJECT和TARGETS的ExcludedArchitect
- 解读Servlet原理篇二---GenericServlet与HttpServlet
周凡杨
javaHttpServlet源理GenericService源码
在上一篇《解读Servlet原理篇一》中提到,要实现javax.servlet.Servlet接口(即写自己的Servlet应用),你可以写一个继承自javax.servlet.GenericServletr的generic Servlet ,也可以写一个继承自java.servlet.http.HttpServlet的HTTP Servlet(这就是为什么我们自定义的Servlet通常是exte
- MySQL性能优化
bijian1013
数据库mysql
性能优化是通过某些有效的方法来提高MySQL的运行速度,减少占用的磁盘空间。性能优化包含很多方面,例如优化查询速度,优化更新速度和优化MySQL服务器等。本文介绍方法的主要有:
a.优化查询
b.优化数据库结构
- ThreadPool定时重试
dai_lm
javaThreadPoolthreadtimertimertask
项目需要当某事件触发时,执行http请求任务,失败时需要有重试机制,并根据失败次数的增加,重试间隔也相应增加,任务可能并发。
由于是耗时任务,首先考虑的就是用线程来实现,并且为了节约资源,因而选择线程池。
为了解决不定间隔的重试,选择Timer和TimerTask来完成
package threadpool;
public class ThreadPoolTest {
- Oracle 查看数据库的连接情况
周凡杨
sqloracle 连接
首先要说的是,不同版本数据库提供的系统表会有不同,你可以根据数据字典查看该版本数据库所提供的表。
select * from dict where table_name like '%SESSION%';
就可以查出一些表,然后根据这些表就可以获得会话信息
select sid,serial#,status,username,schemaname,osuser,terminal,ma
- 类的继承
朱辉辉33
java
类的继承可以提高代码的重用行,减少冗余代码;还能提高代码的扩展性。Java继承的关键字是extends
格式:public class 类名(子类)extends 类名(父类){ }
子类可以继承到父类所有的属性和普通方法,但不能继承构造方法。且子类可以直接使用父类的public和
protected属性,但要使用private属性仍需通过调用。
子类的方法可以重写,但必须和父类的返回值类
- android 悬浮窗特效
肆无忌惮_
android
最近在开发项目的时候需要做一个悬浮层的动画,类似于支付宝掉钱动画。但是区别在于,需求是浮出一个窗口,之后边缩放边位移至屏幕右下角标签处。效果图如下:
一开始考虑用自定义View来做。后来发现开线程让其移动很卡,ListView+动画也没法精确定位到目标点。
后来想利用Dialog的dismiss动画来完成。
自定义一个Dialog后,在styl
- hadoop伪分布式搭建
林鹤霄
hadoop
要修改4个文件 1: vim hadoop-env.sh 第九行 2: vim core-site.xml <configuration> &n
- gdb调试命令
aigo
gdb
原文:http://blog.csdn.net/hanchaoman/article/details/5517362
一、GDB常用命令简介
r run 运行.程序还没有运行前使用 c cuntinue
- Socket编程的HelloWorld实例
alleni123
socket
public class Client
{
public static void main(String[] args)
{
Client c=new Client();
c.receiveMessage();
}
public void receiveMessage(){
Socket s=null;
BufferedRea
- 线程同步和异步
百合不是茶
线程同步异步
多线程和同步 : 如进程、线程同步,可理解为进程或线程A和B一块配合,A执行到一定程度时要依靠B的某个结果,于是停下来,示意B运行;B依言执行,再将结果给A;A再继续操作。 所谓同步,就是在发出一个功能调用时,在没有得到结果之前,该调用就不返回,同时其它线程也不能调用这个方法
多线程和异步:多线程可以做不同的事情,涉及到线程通知
&
- JSP中文乱码分析
bijian1013
javajsp中文乱码
在JSP的开发过程中,经常出现中文乱码的问题。
首先了解一下Java中文问题的由来:
Java的内核和class文件是基于unicode的,这使Java程序具有良好的跨平台性,但也带来了一些中文乱码问题的麻烦。原因主要有两方面,
- js实现页面跳转重定向的几种方式
bijian1013
JavaScript重定向
js实现页面跳转重定向有如下几种方式:
一.window.location.href
<script language="javascript"type="text/javascript">
window.location.href="http://www.baidu.c
- 【Struts2三】Struts2 Action转发类型
bit1129
struts2
在【Struts2一】 Struts Hello World http://bit1129.iteye.com/blog/2109365中配置了一个简单的Action,配置如下
<!DOCTYPE struts PUBLIC
"-//Apache Software Foundation//DTD Struts Configurat
- 【HBase十一】Java API操作HBase
bit1129
hbase
Admin类的主要方法注释:
1. 创建表
/**
* Creates a new table. Synchronous operation.
*
* @param desc table descriptor for table
* @throws IllegalArgumentException if the table name is res
- nginx gzip
ronin47
nginx gzip
Nginx GZip 压缩
Nginx GZip 模块文档详见:http://wiki.nginx.org/HttpGzipModule
常用配置片段如下:
gzip on; gzip_comp_level 2; # 压缩比例,比例越大,压缩时间越长。默认是1 gzip_types text/css text/javascript; # 哪些文件可以被压缩 gzip_disable &q
- java-7.微软亚院之编程判断俩个链表是否相交 给出俩个单向链表的头指针,比如 h1 , h2 ,判断这俩个链表是否相交
bylijinnan
java
public class LinkListTest {
/**
* we deal with two main missions:
*
* A.
* 1.we create two joined-List(both have no loop)
* 2.whether list1 and list2 join
* 3.print the join
- Spring源码学习-JdbcTemplate batchUpdate批量操作
bylijinnan
javaspring
Spring JdbcTemplate的batch操作最后还是利用了JDBC提供的方法,Spring只是做了一下改造和封装
JDBC的batch操作:
String sql = "INSERT INTO CUSTOMER " +
"(CUST_ID, NAME, AGE) VALUES (?, ?, ?)";
- [JWFD开源工作流]大规模拓扑矩阵存储结构最新进展
comsci
工作流
生成和创建类已经完成,构造一个100万个元素的矩阵模型,存储空间只有11M大,请大家参考我在博客园上面的文档"构造下一代工作流存储结构的尝试",更加相信的设计和代码将陆续推出.........
竞争对手的能力也很强.......,我相信..你们一定能够先于我们推出大规模拓扑扫描和分析系统的....
- base64编码和url编码
cuityang
base64url
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.io.StringWriter;
import java.io.UnsupportedEncodingException;
- web应用集群Session保持
dalan_123
session
关于使用 memcached 或redis 存储 session ,以及使用 terracotta 服务器共享。建议使用 redis,不仅仅因为它可以将缓存的内容持久化,还因为它支持的单个对象比较大,而且数据类型丰富,不只是缓存 session,还可以做其他用途,一举几得啊。1、使用 filter 方法存储这种方法比较推荐,因为它的服务器使用范围比较多,不仅限于tomcat ,而且实现的原理比较简
- Yii 框架里数据库操作详解-[增加、查询、更新、删除的方法 'AR模式']
dcj3sjt126com
数据库
public function getMinLimit () { $sql = "..."; $result = yii::app()->db->createCo
- solr StatsComponent(聚合统计)
eksliang
solr聚合查询solr stats
StatsComponent
转载请出自出处:http://eksliang.iteye.com/blog/2169134
http://eksliang.iteye.com/ 一、概述
Solr可以利用StatsComponent 实现数据库的聚合统计查询,也就是min、max、avg、count、sum的功能
二、参数
- 百度一道面试题
greemranqq
位运算百度面试寻找奇数算法bitmap 算法
那天看朋友提了一个百度面试的题目:怎么找出{1,1,2,3,3,4,4,4,5,5,5,5} 找出出现次数为奇数的数字.
我这里复制的是原话,当然顺序是不一定的,很多拿到题目第一反应就是用map,当然可以解决,但是效率不高。
还有人觉得应该用算法xxx,我是没想到用啥算法好...!
还有觉得应该先排序...
还有觉
- Spring之在开发中使用SpringJDBC
ihuning
spring
在实际开发中使用SpringJDBC有两种方式:
1. 在Dao中添加属性JdbcTemplate并用Spring注入;
JdbcTemplate类被设计成为线程安全的,所以可以在IOC 容器中声明它的单个实例,并将这个实例注入到所有的 DAO 实例中。JdbcTemplate也利用了Java 1.5 的特定(自动装箱,泛型,可变长度
- JSON API 1.0 核心开发者自述 | 你所不知道的那些技术细节
justjavac
json
2013年5月,Yehuda Katz 完成了JSON API(英文,中文) 技术规范的初稿。事情就发生在 RailsConf 之后,在那次会议上他和 Steve Klabnik 就 JSON 雏形的技术细节相聊甚欢。在沟通单一 Rails 服务器库—— ActiveModel::Serializers 和单一 JavaScript 客户端库——&
- 网站项目建设流程概述
macroli
工作
一.概念
网站项目管理就是根据特定的规范、在预算范围内、按时完成的网站开发任务。
二.需求分析
项目立项
我们接到客户的业务咨询,经过双方不断的接洽和了解,并通过基本的可行性讨论够,初步达成制作协议,这时就需要将项目立项。较好的做法是成立一个专门的项目小组,小组成员包括:项目经理,网页设计,程序员,测试员,编辑/文档等必须人员。项目实行项目经理制。
客户的需求说明书
第一步是需
- AngularJs 三目运算 表达式判断
qiaolevip
每天进步一点点学习永无止境众观千象AngularJS
事件回顾:由于需要修改同一个模板,里面包含2个不同的内容,第一个里面使用的时间差和第二个里面名称不一样,其他过滤器,内容都大同小异。希望杜绝If这样比较傻的来判断if-show or not,继续追究其源码。
var b = "{{",
a = "}}";
this.startSymbol = function(a) {
- Spark算子:统计RDD分区中的元素及数量
superlxw1234
sparkspark算子Spark RDD分区元素
关键字:Spark算子、Spark RDD分区、Spark RDD分区元素数量
Spark RDD是被分区的,在生成RDD时候,一般可以指定分区的数量,如果不指定分区数量,当RDD从集合创建时候,则默认为该程序所分配到的资源的CPU核数,如果是从HDFS文件创建,默认为文件的Block数。
可以利用RDD的mapPartitionsWithInd
- Spring 3.2.x将于2016年12月31日停止支持
wiselyman
Spring 3
Spring 团队公布在2016年12月31日停止对Spring Framework 3.2.x(包含tomcat 6.x)的支持。在此之前spring团队将持续发布3.2.x的维护版本。
请大家及时准备及时升级到Spring
- fis纯前端解决方案fis-pure
zccst
JavaScript
作者:zccst
FIS通过插件扩展可以完美的支持模块化的前端开发方案,我们通过FIS的二次封装能力,封装了一个功能完备的纯前端模块化方案pure。
1,fis-pure的安装
$ fis install -g fis-pure
$ pure -v
0.1.4
2,下载demo到本地
git clone https://github.com/hefangshi/f