【背包DP】牛客-吉林大学ACM集训队选拔赛（重现赛）B题：Subset of Five

牛客题目传送门


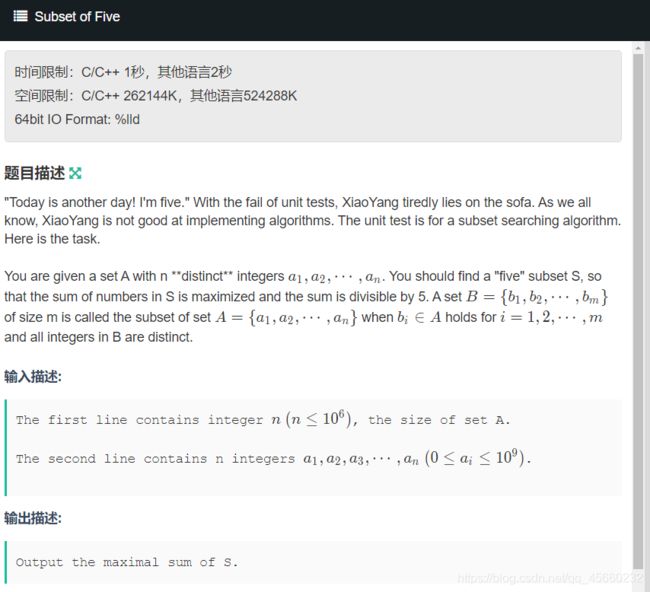
题目大意：在由给定数组中的若干个元素组成的和中找到对5取余等于零的最大的那个和。

这个题呢，比赛的时候没写出来，一直超时，赛后看了一些大佬的代码，好像明白了一点，来做个记录吧。
接下来给分析一下：首先用一个变量s把数组中的和给记录下来，如果s%5==0，直接输出s就行，其实接下来的操作中也包含了这个操作所得的答案。
重头戏：$s$%$5!=0$的情况，领这个余数为 $r$ 我们要想办法把这个余数给消掉，并且要保证消掉这个余数所消耗的代价最小（这里所言的代价就是指在n项中找到若干项的和对$5$取余等于$r$的最小的那个和）。这里就巧妙的用到了背包$DP$，类似于$01$背包，考虑选与不选的情况，然后找到最优策略。
根据代码的话可能更容易理解一点。
按照我一开是的思路，也是想着怎样把那个余数给消掉，当时仅能想到$DFS$暴力来做，直接就超时了，现在学到个$dp$解法挺好，$hh$.

这里给出两种代码思路：
$1$、直接就是正向来考虑，找到$dp[n][0]$的最大值，此最大值就是答案；
$2$、反向来考虑，找到$dp[n][$sum % $5$]的最小值,$sum-$dp[n][$sum % $5$]即为答案
核心思路是一样的，这里再稍微解释一下：
关键就是这句代码：

  dp[i][j]=max(dp[i-1][j],dp[i-1][((j-a[i])%5+5)%5]+a[i]);

余数为$j$,其实它可以有两种来源，一、不选择$a[i]$ 这一项，则价值$dp[i][j]$就是和上一项$dp[i-1][j]$的价值是一样的、选择$a[i]$这一项说明,在没选择这一项时状态的余数$+a[i]$后对$5$取余的余数$j$，则选择$a[i]$的价值是不选择$a[i]$时的价值加上$a[i]$,即$dp[i][j]$=$dp[i-1]$[(($j-a[i]$)%$5$+$5$)%$5$]。
对于这两种情况贪心就可，正向的话就贪最大值，反向的话就贪最小值

上正向考虑代码：

#include
#include
#include
#include
typedef long long ll;
using namespace std;
const int N=1000010;
ll dp[N][5],a[N];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&a[i]);
    }
    memset(dp,-0x3f,sizeof dp);
    dp[0][0]=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=4;j++)
        {
            dp[i][j]=max(dp[i-1][j],dp[i-1][((j-a[i])%5+5)%5]+a[i]);
        }
    }
    printf("%lld",dp[n][0]);
    return 0;
}

再来看一下这一句代码

dp[i][j]=max(dp[i-1][j],dp[i-1][((j-a[i])%5+5)%5]+a[i]);

我们可以发现，我们利用的就只是这一个状态和上一个状态，简单来说，就是指$i$这个状态和$i-1$这个状态,对于上面的这个代码其实还可以对空间进行一步优化，这里可以想到，只利用两个状态，我们用一个滚动数组来存的话比较方便。下面也附上代码，不过是正向考虑的代码，反向的话，这个方法也同样适用，我就不给代码了。

上正向考虑空间优化版的代码

#include
#include
#include
#include
typedef long long ll;
using namespace std;
const int N=1000010;
ll dp[2][5],a[N];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&a[i]);
    }
    memset(dp,-0x3f,sizeof dp);
    dp[0][0]=0;
    int it=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=4;j++)
        {
            dp[!it][j]=max(dp[it][j],dp[it][((j-a[i])%5+5)%5]+a[i]);
        }
        it=!it;
    }
    printf("%lld",dp[n&1][0]);
    return 0;
}

给个图对比一下，可以发现，使用内存方面差别确实挺大的。

上反向考虑代码：

#include
using namespace std;
typedef long long ll;
const int N=1000010;
ll a[N],n;
ll dp[N][6];
int main()
{
	ll s=0;
	scanf("%lld",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&a[i]);
		s+=a[i];
	}
	if(s%5==0) printf("%lld",s);
	else{
		/*二维背包*/
		/*dp[i][j]表示前i个数中选取如干个是组成的和对5取余余数为j的最小的那个和*/ 
		memset(dp,0x3f,sizeof dp);
		dp[0][0]=0;
		for(int i=1;i<=n;i++)
		{
			for(int j=0;j<=4;j++)
			{
				dp[i][j]=min(dp[i-1][j],dp[i-1][(((j-a[i])%5)+5)%5]+a[i]);
				/*  (((j-a[i])%5)+5)%5 这里这一串操作是为了保证余数是非负数 */
			}
		}
		printf("%lld\n",s-dp[n][s%5]);
	}
	return 0;
 }