线性代数及其应用知识点汇总(Linear Algebra and Its Applications)
文章目录
- 线性方程组(Linear Equations in Linear Algebra)
- 矩阵代数(Matrix Algebra)
- 行列式(Determinants)
- 向量空间(Vector Spaces)
- 特征值与特征向量(Eigenvalues and Eigenvectors)
- 正交性和最小二乘法(Orthogonality and Least Squares)
- 对称矩阵和二次型(Symmetric Matrices and Quadratic Forms)
- 奇异值分解(Singular Value Decomposition,SVD)
- 主成分分析(Principle Component Analysis,PCA)
- 向量空间几何学(The Geometry of Vector Spaces)
线性方程组(Linear Equations in Linear Algebra)

初等行变换等价于左乘初等矩阵,初等列变换等价于右乘初等矩阵。
线性方程组的解
线性方程组 A x = b A\boldsymbol x=\boldsymbol b Ax=b有解,当且仅当 b \boldsymbol b b是 A A A的各列的线性组合,即
x 1 a 1 + x 2 a 2 + ⋯ + x n a n = b x_1\boldsymbol a_1 + x_2\boldsymbol a_2+\cdots+x_n\boldsymbol a_n=\boldsymbol b x1a1+x2a2+⋯+xnan=b
线性方程组的解集
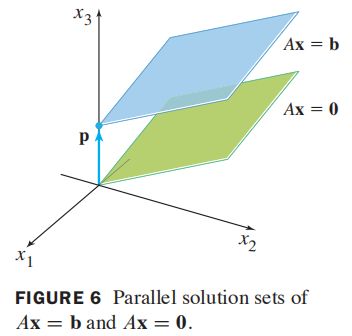
设线性方程组 A x = b A\boldsymbol x=\boldsymbol b Ax=b的一个特解是 p \boldsymbol p p,则 A x = b A\boldsymbol x=\boldsymbol b Ax=b的解集是所有形如 w = p + v h \boldsymbol w=\boldsymbol p+\boldsymbol v_h w=p+vh的向量的集,其中 v h \boldsymbol v_h vh是齐次线性方程组 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0的任意解。
线性相关和线性无关
若 x 1 v 1 + ⋯ + x p v p = 0 x_1\boldsymbol v_1+\cdots+x_p\boldsymbol v_p=0 x1v1+⋯+xpvp=0仅有平凡解(全零解),则称 { v 1 , ⋯ , v p } \{\boldsymbol v_1,\cdots,\boldsymbol v_p\} {v1,⋯,vp}线性无关,若存在不全零解,则称 { v 1 , ⋯ , v p } \{\boldsymbol v_1,\cdots,\boldsymbol v_p\} {v1,⋯,vp}线性相关。特殊地,若 A x = 0 A\boldsymbol x=0 Ax=0仅有零解,则矩阵 A A A的列线性无关。
线性变换
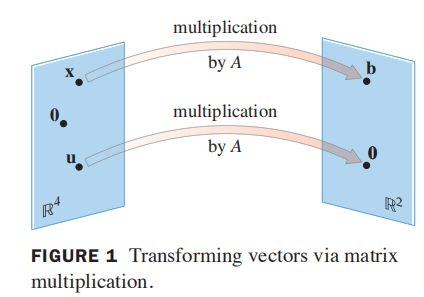
解线性方程 A x = b A\boldsymbol x=\boldsymbol b Ax=b的意义就是找到所有向量 x ∈ R n \boldsymbol x\in \R^n x∈Rn,其左乘线性变换矩阵 A ∈ R m × n A\in\R^{m\times n} A∈Rm×n,可转换为 b ∈ R m \boldsymbol b\in\R^m b∈Rm。定义变换 T : R n → R m T: \R^n\to \R^m T:Rn→Rm为 T ( x ) = A x T(x)=Ax T(x)=Ax,对于变换的应用有以下几类问题:
- 求 u \boldsymbol u u在变换 T T T下的像,即求 T ( x ) T(\boldsymbol x) T(x);
- 求 x ∈ R n \boldsymbol x\in\R^n x∈Rn使它的像是向量 b ∈ R m \boldsymbol b\in\R^m b∈Rm,即求方程 A x = b A\boldsymbol x=\boldsymbol b Ax=b的解;
- 求 c ∈ R m \boldsymbol c\in\R^m c∈Rm是否属于变换 T T T的值域,即求 A x = c A\boldsymbol x=\boldsymbol c Ax=c是否有解;
若 T T T是线性变换,则具有以下性质:
- T ( 0 ) = 0 T(\boldsymbol 0)=\boldsymbol 0 T(0)=0;
- T ( c u + d v ) = c T ( u ) + d T ( v ) T(c\boldsymbol u+d\boldsymbol v)=cT(\boldsymbol u)+dT(\boldsymbol v) T(cu+dv)=cT(u)+dT(v);
线性变换的矩阵
若已知变换 T ( x 1 ) = b 1 T(x_1)=b_1 T(x1)=b1, T ( x 2 ) = b 2 T(x_2)=b_2 T(x2)=b2,则 A X = B AX=B AX=B,若 X X X可逆,则 A = B X ⊤ A=BX^\top A=BX⊤。
矩阵代数(Matrix Algebra)
可逆矩阵
对于矩阵 A n × n A_{n\times n} An×n,若存在矩阵 C n × n C_{n\times n} Cn×n使得, A C = I AC=I AC=I, C A = I CA=I CA=I,则 A A A可逆,逆矩阵为 C C C。可逆矩阵有时称为非奇异矩阵,不可逆矩阵有时称为奇异矩阵。
初等行变换增广矩阵, [ A I ] ∼ [ I A − 1 ] [A\ I] \sim [I\ A^{-1}] [A I]∼[I A−1]。实际很少直接计算逆矩阵,对于求解线性方程组 A x = b Ax=b Ax=b,通过逆矩阵求解 x = A − 1 b x=A^{-1}b x=A−1b的时间复杂度,约是通过行化简复杂度的3倍。
分块矩阵的逆
A − 1 = [ A 11 A 12 0 A 22 ] − 1 = [ A 11 − 1 − A 11 − 1 A 12 A 22 − 1 0 A 22 − 1 ] A^{-1}= \begin{bmatrix} A_{11} &A_{12}\\[1ex] 0 &A_{22} \end{bmatrix}^{-1}= \begin{bmatrix} A_{11}^{-1} &-A_{11}^{-1}A_{12}A_{22}^{-1}\\[1ex] 0 &A_{22}^{-1} \end{bmatrix} A−1=[A110A12A22]−1=[A11−10−A11−1A12A22−1A22−1]
可用初等行变化求解。
LU分解
LU分解用于求解一系列具有相同系数矩阵的线性方程,如 A x = b 1 A\boldsymbol x=\boldsymbol b_1 Ax=b1, A x = b 2 A\boldsymbol x=\boldsymbol b_2 Ax=b2等。实际求解过程中,第一个方程的解是通过行化简得到,为加速计算具有相同系数矩阵的线性方程,在求解第一个方程时得到系数矩阵的LU分解,用于后序计算。

利用A的LU分解(A行倍加变换为U),L为单位下三角矩阵,U为上三角矩阵,可将线性方程组 A x = b Ax=b Ax=b转换为 L ( U x ) = b L(Ux)=b L(Ux)=b,由于L和U都是三角矩阵,通过初等行变换求解方程组的解计算量较小。
行列式(Determinants)
A n × n = [ a i j ] A_{n\times n}=[a_{ij}] An×n=[aij]的行列式按第一行展开得
det A = a 11 det A 11 − a 12 det A 12 + ⋯ + ( − 1 ) 1 + n a 1 n det A 1 n = ∑ j = 1 n ( − 1 ) 1 + j a 1 j det A 1 j \det A=a_{11}\det A_{11} - a_{12}\det A_{12} + \cdots+(-1)^{1+n}a_{1n}\det A_{1n}=\sum_{j=1}^n(-1)^{1+j}a_{1j}\det A_{1j} detA=a11detA11−a12detA12+⋯+(−1)1+na1ndetA1n=j=1∑n(−1)1+ja1jdetA1j
其中 A i j A_{ij} Aij表示矩阵 A A A删除 a i j a_{ij} aij所在行列得到的余子式。
行列式的性质
- A A A的某一行的倍数加到另一行得到 B B B,则 A A A和 B B B的行列式不变;
- A A A的两行互换得到 B B B,则 A A A的行列式是 B B B行列式的相反数;
- A A A的某行乘以 k k k倍得到 B B B,则 B B B行列式是 A A A行列式的 k k k倍;
- A A A的转置是 B B B,则 A A A和 B B B的行列式相同;
- A A A和 B B B均为 n n n阶矩阵,则 det A B = det A det B \det AB=\det A\det B detAB=detAdetB;
伴随矩阵、逆矩阵和克拉默法则
设 A A A是一个 n n n阶可逆矩阵, C i j C_{ij} Cij是矩阵 A A A去除 a i j a_{ij} aij所在行列后的代数余子式的行列式,则
A − 1 = 1 det A adj A , adj A = [ C 11 C 21 ⋯ C n 1 C 12 C 22 ⋯ C n 2 ⋮ ⋱ C 1 n C 2 n ⋯ C n n ] A^{-1}=\frac{1}{\det A}\text{adj}\ A,\quad \text{adj}\ A= \begin{bmatrix} C_{11} & C_{21} &\cdots &C_{n1}\\ C_{12} & C_{22} &\cdots &C_{n2}\\ \vdots & &\ddots\\ C_{1n} & C_{2n}& \cdots &C_{nn} \end{bmatrix} A−1=detA1adj A,adj A=⎣⎢⎢⎢⎡C11C12⋮C1nC21C22C2n⋯⋯⋱⋯Cn1Cn2Cnn⎦⎥⎥⎥⎤
设 A n × n A_{n\times n} An×n是可逆矩阵, b ∈ R n \boldsymbol b\in\R^n b∈Rn,方程 A x = b A\boldsymbol x=\boldsymbol b Ax=b的唯一解是(可利用伴随矩阵表示逆矩阵推出)
x i = det A i ( b ) det A , i = 1 , 2 , ⋯ , n A i ( b ) = [ a 1 ⋯ b ⋯ a n ] x_i=\frac{\det A_i(\boldsymbol b)}{\det A},\quad i=1,2,\cdots,n \quad A_i(\boldsymbol b)=[\boldsymbol a_1\ \cdots\ \boldsymbol b\ \cdots\ \boldsymbol a_n] xi=detAdetAi(b),i=1,2,⋯,nAi(b)=[a1 ⋯ b ⋯ an]
克拉默法则,可用来研究当 b \boldsymbol b b或 A A A中某元素改变时, A x = b A\boldsymbol x=\boldsymbol b Ax=b解的变化。如 A A A第 i i i列元素改变时, A x = b A\boldsymbol x=\boldsymbol b Ax=b解的第 i i i位置不变,其它所有位置可能改变。
行列式的几何意义
二阶行列式表示,两个列向量围成的二维平面的面积;三阶行列式表示,三个列向量围成的三维 六面体的体积。
向量空间(Vector Spaces)
向量空间
一个向量空间是向量的非空集合,这个集合中各向量的加法和标量乘法运算封闭。
矩阵零空间
矩阵 A A A的零空间记成 Nul A \text{Nul}\ A Nul A,是齐次方程 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0的解集,即
Nul A = { x ; x ∈ R n , A x = 0 } \text{Nul}\ A=\{\boldsymbol x;\boldsymbol x\in\R^n,A\boldsymbol x=\boldsymbol 0\} Nul A={x;x∈Rn,Ax=0}
零空间中包含自由向量的个数,等于方程 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0中自由变量的个数。
矩阵的列空间
矩阵 A m × n A_{m\times n} Am×n的列空间是由 A A A的列的所有线性组合组成的集合,记为
Col A = Span { a 1 , ⋯ , a n } , Col A ∈ R n \text{Col }A=\text{Span }\{\boldsymbol a_1,\cdots,\boldsymbol a_n\},\quad \text{Col }A\in\R^n Col A=Span {a1,⋯,an},Col A∈Rn
矩阵列空间是线性变换 A x A\boldsymbol x Ax的值域。
坐标系
唯一表示定理: B = { b 1 , ⋯ , b n } \Beta=\{\boldsymbol b_1,\cdots,\boldsymbol b_n\} B={b1,⋯,bn}是向量空间 V V V的一个基,则对于 V V V中的每一个向量 x \boldsymbol x x,存在唯一一组数 c 1 , ⋯ , c n {c_1,\cdots,c_n} c1,⋯,cn使得
x = c 1 b 1 + ⋯ + c n b n \boldsymbol x=c_1\boldsymbol b_1+\cdots+c_n\boldsymbol b_n x=c1b1+⋯+cnbn
秩
矩阵 A m × n A_{m\times n} Am×n的秩等于列空间的维数,等于行空间的维数,且满足
rank A + dim Nul A = n \text{rank }A+\dim\text{Nul }A = n rank A+dimNul A=n
由于计算机存储精度问题,矩阵的有效秩常由奇异值分解确定,通过奇异值分解还可以可靠地求解列空间、行空间和零空间的基。
马尔科夫链的收敛性
若 P P P是一个 n × n n\times n n×n的正则随机矩阵,则 P P P具有唯一的稳态向量 q \boldsymbol q q,若 x 0 \boldsymbol x_0 x0是任一个初始状态,且 x k + 1 = P x k \boldsymbol x_{k+1}=P\boldsymbol x_k xk+1=Pxk,则当 k k k趋于无穷时,马尔科夫链 { x k } \{\boldsymbol x_k\} {xk}收敛到 q \boldsymbol q q。
特征值与特征向量(Eigenvalues and Eigenvectors)
A A A为 n × n n\times n n×n矩阵, x \boldsymbol x x为非零向量,若存在数 λ \lambda λ使 A x = λ x A\boldsymbol x=\lambda \boldsymbol x Ax=λx有非平凡解,则称 λ \lambda λ为 A A A的特征值, x \boldsymbol x x为对应 λ \lambda λ的特征向量。
若 x \boldsymbol x x是A的特征向量, A x A\boldsymbol x Ax相当于将 x \boldsymbol x x拉长 λ \lambda λ倍。
对于齐次线性方程组
( A − λ I ) x = 0 (A-\lambda I)\boldsymbol x=\boldsymbol 0 (A−λI)x=0
,其解空间/零空间是特征向量集合。
三角矩阵的特征值
三角矩阵的主对角线的元素是其特征值。

当 λ \lambda λ等于任意对角线元素值时,对角线元素为0,对应于 ( A − λ I ) x = 0 (A-\lambda I)x=0 (A−λI)x=0的自由变量,即存在非平凡解,即 A x = a i i x Ax=a_{ii}x Ax=aiix,即对角线元素 a i i a_{ii} aii为特征值。
可逆与特征值
设 A A A是 n n n阶矩阵,则 A A A可逆当且仅当
- 0不是 A A A的特征值;
- A A A的行列式不等于0;
特征方程
数值方程 det ( A − λ I ) = 0 \det(A-\lambda I)=0 det(A−λI)=0,称为 A A A的特征方程, λ \lambda λ是矩阵 A A A的特征值的充要条件是 λ \lambda λ是其特征方程的根。
相似矩阵与相似变换
假设 A A A和 B B B都是 n × n n\times n n×n矩阵,若存在可逆矩阵 P P P,使得 P − 1 A P = B P^{-1}AP=B P−1AP=B,则称 A A A相似于 B B B, P P P称为相似变换矩阵。相似矩阵具有相同特征多项式,具有相同特征值(实际计算特征值,一般计算相似矩阵的特征值)。
证明:若 A A A和 B B B相似,则 B = P − 1 A P B=P^{-1}AP B=P−1AP,则
B − λ I = P − 1 A P − λ P − 1 P = P − 1 ( A − λ I ) P B-\lambda I=P^{-1}AP-\lambda P^{-1}P=P^{-1}(A-\lambda I)P B−λI=P−1AP−λP−1P=P−1(A−λI)P
因此
det ( B − λ I ) = det P − 1 det ( A − λ I ) det P = det ( A − λ I ) \det (B-\lambda I)=\det P^{-1}\det (A-\lambda I)\det P=\det (A-\lambda I) det(B−λI)=detP−1det(A−λI)detP=det(A−λI)
对角化(用途、条件、对角化过程)
通过将矩阵 A A A对角化,即 A = P D P − 1 A=PDP^{-1} A=PDP−1,其中 D D D为对角矩阵,能够获得矩阵 A A A的特征值和特征向量信息,也能够快速计算 A k A^k Ak。
若矩阵 A A A是 n n n阶矩阵, A A A可对角化的充要条件是其有 n n n个线性无关的特征向量。对角化的核心是 A P = P D AP=PD AP=PD,求解 A A A的特征值和特征向量,以特征向量作为列向量构造 P P P矩阵,以对应的特征值作为对角元素构造对角矩阵 D D D。
特征值迭代估计
1.幂算法 适用于 n × n n\times n n×n矩阵 A A A有严格占优特征值,即主特征值。假设 x ∈ R n \boldsymbol x\in\R^n x∈Rn,特征向量集合 { v 1 , ⋯ , v 2 } \{\boldsymbol v_1,\cdots,\boldsymbol v_2\} {v1,⋯,v2}作为基, x = c 1 v 1 + ⋯ + c n v n \boldsymbol x=c_1\boldsymbol v_1+\cdots+c_n\boldsymbol v_n x=c1v1+⋯+cnvn,则
x k = A k x = c 1 λ 1 k v 1 + c 2 λ 2 k v 2 + ⋯ + c n λ n k v k \boldsymbol x_k=A^k\boldsymbol x=c_1\lambda_1^k\boldsymbol v_1+c_2\lambda_2^k\boldsymbol v_2+\cdots+c_n\lambda_n^k\boldsymbol v_k xk=Akx=c1λ1kv1+c2λ2kv2+⋯+cnλnkvk
假设 c 1 c_1 c1不为0,当 k → + ∞ k\to +\infty k→+∞, A k x A^k\boldsymbol x Akx的方向将趋向于 v 1 \boldsymbol v_1 v1,且满足 A ⋅ A k − 1 x = λ 1 v 1 A\cdot A^{k-1}\boldsymbol x=\lambda_1\boldsymbol v_1 A⋅Ak−1x=λ1v1。不难得出, x k − 1 ≈ v 1 \boldsymbol x_{k-1}\approx \boldsymbol v_1 xk−1≈v1,也就是说, x k \boldsymbol x_k xk最大分量相较于 x k − 1 \boldsymbol x_{k-1} xk−1最大分量增加的倍数接近于 λ 1 \lambda_1 λ1。若令特征向量的最大分量为1,则 x k \boldsymbol x_k xk的最大分量为特征值, x k \boldsymbol x_k xk除最大分量为特征向量。
2.逆幂法 适用于已知一个特征值的初始估计值 α \alpha α,求近似精确值。具体做法是对 B = ( A − α I ) − 1 B=(A-\alpha I)^{-1} B=(A−αI)−1应用幂算法,求解过程:
- 选择一个非常接近于 λ \lambda λ的初始估值 α \alpha α;
- 选择一个最大分量为1的初始向量 x 0 \boldsymbol x_0 x0;
- 对 k = 0 , 1 , ⋯ , k=0,1,\cdots, k=0,1,⋯,
- 从 ( A − α I ) y k = x k (A-\alpha I)\boldsymbol y_k=\boldsymbol x_k (A−αI)yk=xk解出 y k \boldsymbol y_k yk, y k \boldsymbol y_k yk最大分量为 μ k \mu_k μk,同系数线性方程组,使用LU分解可加速计算;
- 计算 v k = α + ( 1 / u k ) v_k=\alpha+(1/u_k) vk=α+(1/uk),近似特征值;
- 计算 x k + 1 = ( 1 / u k ) y k \boldsymbol x_{k+1}=(1/u_k)\boldsymbol y_k xk+1=(1/uk)yk,规范化 x k x_k xk最大分量为1;
- 几乎对所有选择的 x 0 \boldsymbol x_0 x0,序列 { v k } \{\boldsymbol v_k\} {vk}趋向于 A A A的特征值 λ \lambda λ,而序列 { x k } \{\boldsymbol x_k\} {xk}趋向于对应的特征向量;
正交性和最小二乘法(Orthogonality and Least Squares)
寻找一个没有真正解的不相容的方程组的近似解。
毕达哥拉斯(勾股)定理
两个向量 u \boldsymbol u u和 v \boldsymbol v v正交的充分必要条件是 ∣ ∣ u + v ∣ ∣ 2 = ∣ ∣ u ∣ ∣ 2 + ∣ ∣ v ∣ ∣ 2 ||\boldsymbol u+\boldsymbol v||^2=||\boldsymbol u||^2+||\boldsymbol v||^2 ∣∣u+v∣∣2=∣∣u∣∣2+∣∣v∣∣2。
证明: ∣ ∣ u + v ∣ ∣ 2 = ( u + v ) ⊤ ( u + v ) = 2 u ⊤ v + u ⊤ u + v ⊤ v ||\boldsymbol u+\boldsymbol v||^2=(\boldsymbol u+\boldsymbol v)^\top(\boldsymbol u+\boldsymbol v)=2\boldsymbol u^\top \boldsymbol v+\boldsymbol u^\top\boldsymbol u+\boldsymbol v^\top \boldsymbol v ∣∣u+v∣∣2=(u+v)⊤(u+v)=2u⊤v+u⊤u+v⊤v,若 u \boldsymbol u u和 v \boldsymbol v v正交,则 ∣ ∣ u + v ∣ ∣ 2 = u ⊤ u + v ⊤ v = ∣ ∣ u ∣ ∣ 2 + ∣ ∣ v ∣ ∣ 2 ||\boldsymbol u+\boldsymbol v||^2=\boldsymbol u^\top \boldsymbol u+\boldsymbol v^\top\boldsymbol v=||\boldsymbol u||^2+||\boldsymbol v||^2 ∣∣u+v∣∣2=u⊤u+v⊤v=∣∣u∣∣2+∣∣v∣∣2。
正交补
如果向量 z z z与向量空间 W W W中的任意向量正交,则称 z z z正交于 W W W,所有正交于 W W W的向量 z z z集合称为 W W W的正交补,记为 W ⊥ W^\bot W⊥。对于矩阵 A m × n A_{m\times n} Am×n,则 A A A的行空间的正交补是 A A A的零空间,且 A A A的列空间的正交补是 A ⊤ A^\top A⊤的零空间:
( Row A ) ⊥ = Nul A , ( Col A ) ⊥ = Nul A ⊤ (\text{Row }A)^\bot = \text{Nul }A, \quad (\text{Col }A)^\bot=\text{Nul }A ^\top (Row A)⊥=Nul A,(Col A)⊥=Nul A⊤
证明:由于零空间中的向量 x \boldsymbol x x满足 A x = 0 A\boldsymbol x=\boldsymbol 0 Ax=0,显然 x \boldsymbol x x和 A A A的每一个行向量的内积为0,即正交。
向量间夹角/相关系数
cos θ = u ⋅ v ∣ ∣ u ∣ ∣ ∣ ∣ v ∣ ∣ \cos \theta=\frac{u\cdot v}{||u||\ ||v||} cosθ=∣∣u∣∣ ∣∣v∣∣u⋅v
正交基的坐标表示
假设 { u 1 , ⋯ , u p } \{\boldsymbol u_1,\cdots,\boldsymbol u_p\} {u1,⋯,up}是 R n \R^n Rn子空间 W W W的正交基,对 W W W中的任意向量 y \boldsymbol y y,可表示为
y = c 1 u 1 + ⋯ + c p u p , c j = y ⋅ u j u j ⋅ u j \boldsymbol y=c_1\boldsymbol u_1+\cdots+c_p\boldsymbol u_p,\quad c_j=\frac{\boldsymbol y\cdot\boldsymbol u_j}{\boldsymbol u_j\cdot \boldsymbol u_j} y=c1u1+⋯+cpup,cj=uj⋅ujy⋅uj
其中 c j c_j cj表示 y \boldsymbol y y在基 u j \boldsymbol u_j uj上的投影长度。
正交投影
向量 y \boldsymbol y y在向量 u \boldsymbol u u上的投影为
y ^ = proj L y = y ⋅ u u ⋅ u ⋅ u \hat \boldsymbol y=\text{proj}_L\boldsymbol y=\frac{\boldsymbol y\cdot \boldsymbol u}{\boldsymbol u\cdot \boldsymbol u}\cdot \boldsymbol u y^=projLy=u⋅uy⋅u⋅u
单位正交基
矩阵 U m × n U_{m\times n} Um×n具有单位正交列向量的充分必要条件是, U ⊤ U = I U^\top U=I U⊤U=I。假设 U U U是一个单位正交列的 m × n m\times n m×n矩阵,且 x \boldsymbol x x和 y \boldsymbol y y是 R n \R^n Rn中的向量,则
- ∣ ∣ U x ∣ ∣ = ∣ ∣ x ∣ ∣ ||U\boldsymbol x||=||\boldsymbol x|| ∣∣Ux∣∣=∣∣x∣∣;
- ( U x ) ⋅ ( U y ) = x ⋅ y (U\boldsymbol x)\cdot (U\boldsymbol y)=\boldsymbol x\cdot \boldsymbol y (Ux)⋅(Uy)=x⋅y;
- ( U x ) ⋅ ( U y ) = 0 (U\boldsymbol x)\cdot(U\boldsymbol y)=0 (Ux)⋅(Uy)=0的充要条件是 x ⋅ y = 0 \boldsymbol x\cdot \boldsymbol y=0 x⋅y=0;
当方阵 U U U是单位正交矩阵时, U − 1 = U ⊤ U^{-1}=U^\top U−1=U⊤,单位正交阵的行也正交。
证明: U ⊤ U = I U^\top U=I U⊤U=I, U ⊤ = U − 1 U^\top=U^{-1} U⊤=U−1, U ⋅ U − 1 = U U ⊤ = I U\cdot U^{-1}=UU^\top=I U⋅U−1=UU⊤=I,因此单位正交阵的行向量正交。
空间中的正交投影
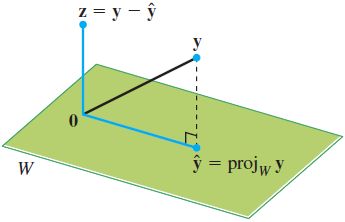
设 W ⊂ R n W\sub\R^n W⊂Rn, ∀ y ∈ R n \forall \boldsymbol y\in \R^n ∀y∈Rn唯一表示为 y = y ^ + z \boldsymbol y=\hat{\boldsymbol y}+\boldsymbol z y=y^+z, y ^ ∈ W \boldsymbol{\hat y}\in W y^∈W, z ∈ W ⊥ \boldsymbol z\in W^{\bot} z∈W⊥,若 W W W的任一正交基为 { u 1 , ⋯ , u p } \{\boldsymbol u_1,\cdots,\boldsymbol u_p\} {u1,⋯,up},则 y \boldsymbol y y在 W W W内的正交投影为
y ^ = proj W y = y ⋅ u 1 u 1 ⋅ u 1 u 1 + ⋯ + y ⋅ u p u p ⋅ u p u p \boldsymbol{\hat y}=\text{proj}_W\boldsymbol y=\frac{\boldsymbol y\cdot \boldsymbol u_1}{\boldsymbol u_1\cdot \boldsymbol u_1}\boldsymbol u_1+\cdots+\frac{\boldsymbol y\cdot \boldsymbol u_p}{\boldsymbol u_p\cdot \boldsymbol u_p}\boldsymbol u_p y^=projWy=u1⋅u1y⋅u1u1+⋯+up⋅upy⋅upup
上式每项系数为投影向量对应于基向量 u i \boldsymbol u_i ui的分量/坐标.
最佳逼近定理(Optimal Approximation Theorem)
∀ v ∈ W , v ≠ y ^ = proj W y ⟹ ∣ y − y ^ ∣ < ∣ y − v ∣ \forall \boldsymbol v\in W,\ \boldsymbol v \neq \boldsymbol{\hat y}=\text{proj}_W\boldsymbol y \implies |\boldsymbol y-\boldsymbol {\hat y}| < |\boldsymbol y - \boldsymbol v| ∀v∈W, v=y^=projWy⟹∣y−y^∣<∣y−v∣
定理表明, y \boldsymbol y y在向量空间中的投影向量为 y ^ \hat \boldsymbol y y^,则 W W W中的任一向量到 y \boldsymbol y y的距离均大于投影向量 y ^ \hat \boldsymbol y y^到 y \boldsymbol y y的距离。
施密特正交化(Schmidt Orthogonalization)
向量空间 W ⊂ R n W\subset \R^n W⊂Rn, { x 1 , ⋯ , x p } \{\boldsymbol x_1, \cdots, \boldsymbol x_p\} {x1,⋯,xp}和 { v 1 , ⋯ , v p } \{\boldsymbol v_1, \cdots, \boldsymbol v_p\} {v1,⋯,vp}分别是 W W W的任一基和正交基,
v 1 = x 1 v 2 = x 2 − x 2 ⋅ v 1 v 1 ⋅ v 1 v 1 ⋮ v p = x p − x p ⋅ v 1 v 1 ⋅ v 1 v 1 − ⋯ − x p ⋅ v p − 1 v p − 1 ⋅ v p − 1 v p − 1 \begin{aligned} &\boldsymbol v_1 = \boldsymbol x_1 \\[1ex] &\boldsymbol v_2 = \boldsymbol x_2 - \frac{\boldsymbol x_2 \cdot \boldsymbol v_1}{\boldsymbol v_1 \cdot \boldsymbol v_1}\boldsymbol v_1\\[1ex] &\vdots\\ & \boldsymbol v_p = \boldsymbol x_p - \frac{\boldsymbol x_p \cdot \boldsymbol v_1}{\boldsymbol v_1 \cdot \boldsymbol v_1}\boldsymbol v_1 -\cdots - \frac{\boldsymbol x_p \cdot \boldsymbol v_{p-1}}{\boldsymbol v_{p-1} \cdot \boldsymbol v_{p-1}}\boldsymbol v_{p-1} \end{aligned} v1=x1v2=x2−v1⋅v1x2⋅v1v1⋮vp=xp−v1⋅v1xp⋅v1v1−⋯−vp−1⋅vp−1xp⋅vp−1vp−1
对于基向量 x i \boldsymbol x_i xi,令 x ^ i = proj W i − 1 x i \boldsymbol{\hat x_i} = \text{proj}_{W_{i-1}}\boldsymbol x_i x^i=projWi−1xi, W i − 1 = { x 1 , ⋯ , x i − 1 } W_{i-1}=\{\boldsymbol x_1, \cdots, \boldsymbol x_{i-1}\} Wi−1={x1,⋯,xi−1},则对 x i \boldsymbol x_i xi进行正交分解得
v i = x i − x ^ i , v i ∈ W ⊥ \boldsymbol v_i=\boldsymbol x_i-\boldsymbol{\hat x_i},\quad\boldsymbol v_i\in W^\bot vi=xi−x^i,vi∈W⊥
将 v i \boldsymbol v_i vi作为 x i \boldsymbol x_i xi的正交化向量,依次将 x 2 , ⋯ , x p \boldsymbol x_2, \cdots, \boldsymbol x_p x2,⋯,xp执行以上步骤即可完成。
QR分解(QR Decomposition)
如果矩阵 A m × n A_{m\times n} Am×n的列线性无关,则 A A A可分解为 A = Q R A=QR A=QR,其中 Q Q Q是一个 m × n m\times n m×n矩阵,其列形成 Col A \text{Col }A Col A的一个标准正交基, R R R是一个 n n n阶可逆上三角矩阵,且对角线元素均为正数。
利用施密特正交化,将 A A A标准正交化得到 Q Q Q,由 Q ⊤ Q = I Q^\top Q=I Q⊤Q=I,知上三角矩阵
R = Q ⊤ Q R = Q ⊤ A ⟹ A = Q R R=Q^\top QR=Q^\top A \implies A=QR R=Q⊤QR=Q⊤A⟹A=QR
最小二乘问题(Least Square Solution,LSS)
解不相容线性方程组 A m × n x = b A_{m\times n}\boldsymbol x=\boldsymbol b Am×nx=b, b ∉ Col A \boldsymbol b \notin \text{Col } A b∈/Col A,最优方法是寻找 x \boldsymbol x x,使 A x A\boldsymbol x Ax尽可能接近 b \boldsymbol b b。也就是说, ∀ x ∈ R n \forall \boldsymbol x \in \R^n ∀x∈Rn, A x = b A\boldsymbol x=\boldsymbol b Ax=b的最小二乘解 x ^ \boldsymbol{\hat x} x^应满足( A x A\boldsymbol x Ax表示 b \boldsymbol b b在 A A A列空间中的投影)
∣ ∣ b − A x ^ ∣ ∣ ≤ ∣ ∣ b − A x ∣ ∣ ⟹ A x ^ = b ^ = proj Col A b ||\boldsymbol b - A\boldsymbol{\hat x}|| \leq ||\boldsymbol b-A\boldsymbol x|| \quad\implies\quad A\boldsymbol {\hat x}=\hat{\boldsymbol b}=\text{proj}_{\text{Col }A}\boldsymbol b ∣∣b−Ax^∣∣≤∣∣b−Ax∣∣⟹Ax^=b^=projCol Ab
由正交分解定理知, b − b ^ \boldsymbol b - \boldsymbol{\hat b} b−b^正交于 Col A \text{Col }A Col A,即
A ⊤ ( b − b ^ ) = 0 = A ⊤ ( b − A x ^ ) = 0 ⟹ A ⊤ A x ^ = A ⊤ b A^\top (\boldsymbol b - \boldsymbol{\hat b})=\boldsymbol 0 = A^\top (\boldsymbol b - A\boldsymbol {\hat x})=\boldsymbol 0 \implies A^\top A\boldsymbol{\hat x}=A^\top \boldsymbol b A⊤(b−b^)=0=A⊤(b−Ax^)=0⟹A⊤Ax^=A⊤b
A ⊤ A x ^ = A ⊤ b A^\top A\boldsymbol{\hat x}=A^\top \boldsymbol b A⊤Ax^=A⊤b为原方程的法方程,其解集与原方程最小二乘解集一致, ∣ ∣ b − A x ^ ∣ ∣ ||\boldsymbol b - A\boldsymbol{\hat x}|| ∣∣b−Ax^∣∣称为最小二乘误差。
QR分解与最小二乘(QR Decomposition and LSS)
若 A m × n A_{m\times n} Am×n列线性无关,将 A A A进行QR分解,得
R ⊤ Q ⊤ Q R x ^ = R ⊤ Q ⊤ b ⟹ R x ^ = Q ⊤ b R^\top Q^\top QR\boldsymbol{\hat x}=R^\top Q^\top \boldsymbol b \implies R\boldsymbol {\hat x}=Q^\top \boldsymbol b R⊤Q⊤QRx^=R⊤Q⊤b⟹Rx^=Q⊤b
由于 R R R为上三角可逆矩阵,通过初等行变换求解 x ^ \boldsymbol{\hat x} x^,比公式 x ^ = R − 1 Q ⊤ b \boldsymbol{\hat x}=R^{-1}Q^\top \boldsymbol b x^=R−1Q⊤b更加高效。特别地,若 A A A为正交矩阵,QR分解所得 R R R矩阵为对角矩阵,对角元素为对应列向量的模,最优解 x ^ \hat{\boldsymbol x} x^等价于 b \boldsymbol b b在 A A A列空间正交投影的坐标向量,即
x ^ = [ ⟨ b , a 1 ⟩ ⟨ a 1 , a 1 ⟩ , ⋯ , ⟨ b , a n ⟩ ⟨ a n , a n ⟩ ] ⊤ \boldsymbol{\hat x}=\left[\frac{\langle \boldsymbol b, \boldsymbol a_1\rangle}{\langle \boldsymbol a_1, \boldsymbol a_1\rangle}, \cdots, \frac{\langle \boldsymbol b, \boldsymbol a_n\rangle}{\langle \boldsymbol a_n, \boldsymbol a_n\rangle}\right]^\top x^=[⟨a1,a1⟩⟨b,a1⟩,⋯,⟨an,an⟩⟨b,an⟩]⊤
线性回归(Linear Regression)
给定数据集 X X X和目标值 y y y,求解线性回归模型使得 X w = y Xw=y Xw=y。线性回归模型可认为是求解不相容线性方程组,令 y ^ \hat y y^表示 y y y在 X X X列空间中的投影,因此 y − y ^ y-\hat y y−y^与 Col X \text{Col }X Col X正交,即
X ⊤ ( y − y ^ ) = 0 ⟹ X ⊤ ( y − X w ^ ) = 0 ⟹ w ^ = ( X ⊤ X ) − 1 X ⊤ y X^\top(\boldsymbol y-\hat \boldsymbol y)=0 \implies X^\top(\boldsymbol y-X\hat \boldsymbol w)=0 \implies \hat \boldsymbol w=(X^\top X)^{-1}X^\top \boldsymbol y X⊤(y−y^)=0⟹X⊤(y−Xw^)=0⟹w^=(X⊤X)−1X⊤y
内积空间(Inner Product Spaces)
赋予以下内积的向量空间,称为内积空间:
- ⟨ u , v ⟩ = ⟨ v , u ⟩ \langle u, v\rangle=\langle v, u\rangle ⟨u,v⟩=⟨v,u⟩;
- ⟨ u + v , w ⟩ = ⟨ u , w ⟩ + ⟨ v , w ⟩ \langle u + v, w\rangle=\langle u, w\rangle + \langle v, w\rangle ⟨u+v,w⟩=⟨u,w⟩+⟨v,w⟩;
- ⟨ c u , v ⟩ = c ⟨ u , v ⟩ \langle cu, v\rangle=c\langle u, v\rangle ⟨cu,v⟩=c⟨u,v⟩;
- ⟨ u , u ⟩ ≥ 0 \langle u, u\rangle\geq 0 ⟨u,u⟩≥0, ⟨ u , u ⟩ = 0 \langle u, u\rangle=0 ⟨u,u⟩=0,充要条件是 u = 0 u=0 u=0;
内积空间的最佳逼近
设 t 0 , ⋯ , t n t_0,\cdots,t_n t0,⋯,tn是不同的实数,对 P n \mathbb P_n Pn中的 p p p和 q q q,定义内积为(满足内积空间约束)
⟨ p , q ⟩ = p ( t 0 ) q ( t 0 ) + p ( t 1 ) q ( t 1 ) + ⋯ + p ( t n ) q ( t n ) \langle p,q\rangle=p(t_0)q(t_0)+p(t_1)q(t_1)+\cdots+p(t_n)q(t_n) ⟨p,q⟩=p(t0)q(t0)+p(t1)q(t1)+⋯+p(tn)q(tn)
若 V V V是内积空间中的 P 4 \mathbb P_4 P4,包含多项式-2,-1,0,1和2处的值,则对于多项式 1 1 1, t t t, t 2 t^2 t2,构造 V V V子空间 P 2 \mathbb P_2 P2的标准正交基:
 |
 |
解: 由于内积仅依赖于多项式在-2,-1,0,1和2处的值,则每个多项式 1 1 1, t t t, t 2 t^2 t2对应的 R 5 \R^5 R5向量,如上左图所示。应用格拉姆-施密特方法正交化 1 1 1, t t t, t 2 t^2 t2,由于 1 1 1和 t t t正交,令 p 0 ( t ) = 0 p_0(t)=0 p0(t)=0, p 1 ( t ) = t p_1(t)=t p1(t)=t,现在只需正交化 t 2 t^2 t2即可,即
p 2 ( t ) = t 2 − ⟨ t 2 , p 1 ⟩ ⟨ p 1 , p 1 ⟩ p 1 − ⟨ t 2 , p 0 ⟩ ⟨ p 0 , p 0 ⟩ p 0 = t 2 − ⟨ t 2 , t ⟩ ⟨ t , t ⟩ t − ⟨ t 2 , 1 ⟩ ⟨ 1 , 1 ⟩ 1 = t 2 − 2 p_2(t)=t^2-\frac{\langle t^2,p_1\rangle}{\langle p_1,p_1\rangle}p_1-\frac{\langle t^2,p_0\rangle}{\langle p_0,p_0\rangle}p_0 =t^2-\frac{\langle t^2,t\rangle}{\langle t,t\rangle}t-\frac{\langle t^2,1\rangle}{\langle 1,1\rangle}1=t^2-2 p2(t)=t2−⟨p1,p1⟩⟨t2,p1⟩p1−⟨p0,p0⟩⟨t2,p0⟩p0=t2−⟨t,t⟩⟨t2,t⟩t−⟨1,1⟩⟨t2,1⟩1=t2−2
V V V子空间 P 2 \mathbb P_2 P2的正交基,如上右图所示。
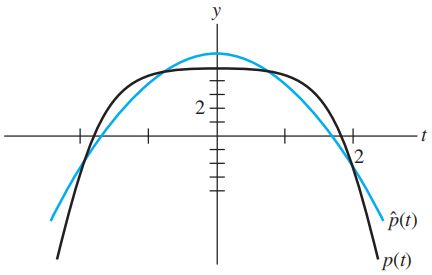
求出 P 2 \mathbb P_2 P2中的多项式对 p ( t ) = 5 − 1 2 t 4 p(t)=5-\dfrac{1}{2}t^4 p(t)=5−21t4的最佳逼近? P 2 \mathbb P_2 P2中多项式对 p ( t ) p(t) p(t)的最佳逼近为 p t p_t pt在 P 2 \mathbb P_2 P2中的投影,由于 p p p在各点的相应取值分别为-3,9/2, 5,9/2和-3,因此
⟨ p , p 0 ⟩ = 8 , ⟨ p , p 1 ⟩ = 0 , ⟨ p , p 2 ⟩ = − 31 ⟹ p ^ = proj P 2 p = ⟨ p , p 0 ⟩ ⟨ p 0 , p 0 ⟩ p 0 + ⟨ p , p 1 ⟩ ⟨ p 1 , p 1 ⟩ p 1 + ⟨ p , p 2 ⟩ ⟨ p 2 , p 2 ⟩ p 2 = 8 5 − 31 14 ( t 2 − 2 ) \langle p,p_0\rangle=8,\ \langle p,p_1\rangle=0,\ \langle p,p_2\rangle=-31 \implies \hat p=\text{proj}_{\mathbb P_2} p=\frac{\langle p,p_0\rangle}{\langle p_0,p_0\rangle}p_0 + \frac{\langle p,p_1\rangle}{\langle p_1,p_1\rangle}p_1 + \frac{\langle p,p_2\rangle}{\langle p_2,p_2\rangle}p_2=\frac{8}{5}-\frac{31}{14}(t^2-2) ⟨p,p0⟩=8, ⟨p,p1⟩=0, ⟨p,p2⟩=−31⟹p^=projP2p=⟨p0,p0⟩⟨p,p0⟩p0+⟨p1,p1⟩⟨p,p1⟩p1+⟨p2,p2⟩⟨p,p2⟩p2=58−1431(t2−2)
柯西-施瓦茨不等式(Cauchy - Schwartz Inequality)
∣ ⟨ u , v ⟩ ∣ ≤ ∣ ∣ u ∣ ∣ ∣ ∣ v ∣ ∣ |\langle\boldsymbol u, \boldsymbol v \rangle|\leq ||\boldsymbol u||\ ||\boldsymbol v|| ∣⟨u,v⟩∣≤∣∣u∣∣ ∣∣v∣∣
证:当 u = 0 \boldsymbol u = \boldsymbol 0 u=0时,不等式显然成立。当 u ≠ 0 \boldsymbol u\neq \boldsymbol 0 u=0时, u \boldsymbol u u生成空间 W W W,则
∣ ∣ proj W v ∣ ∣ = ∣ ∣ ⟨ v , u ⟩ ⟨ u , u ⟩ u ∣ ∣ = ∣ ⟨ v , u ⟩ ∣ ∣ ∣ u ∣ ∣ ≤ ∣ ∣ v ∣ ∣ ⟹ ∣ ⟨ u , v ⟩ ∣ ≤ ∣ ∣ u ∣ ∣ ∣ ∣ v ∣ ∣ ||\text{proj}_W\boldsymbol v || = \left|\left|\frac{\langle\boldsymbol v, \boldsymbol u\rangle}{\langle\boldsymbol u, \boldsymbol u\rangle}\boldsymbol u\right|\right| = \frac{|\langle\boldsymbol v, \boldsymbol u\rangle|}{||\boldsymbol u||} \leq ||\boldsymbol v|| \implies |\langle\boldsymbol u, \boldsymbol v \rangle|\leq ||\boldsymbol u||\ ||\boldsymbol v|| ∣∣projWv∣∣=∣∣∣∣∣∣∣∣⟨u,u⟩⟨v,u⟩u∣∣∣∣∣∣∣∣=∣∣u∣∣∣⟨v,u⟩∣≤∣∣v∣∣⟹∣⟨u,v⟩∣≤∣∣u∣∣ ∣∣v∣∣
也可以向量夹角方向证明,当前仅当两向量同向时,内积取最大值。
三角不等式(Triangle Inequality)
∣ ∣ u + v ∣ ∣ ≤ ∣ ∣ u ∣ ∣ + ∣ ∣ v ∣ ∣ ||\boldsymbol u + \boldsymbol v|| \leq ||\boldsymbol u|| + ||\boldsymbol v|| ∣∣u+v∣∣≤∣∣u∣∣+∣∣v∣∣
证明:
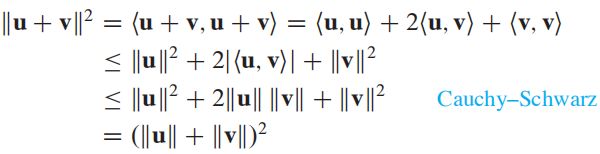
最小二乘应用(Application of Least Square)
对于数据(-2, 3),(-1, 5),(0, 5),(1, 4),(2, 3),求二次、三次最佳逼近,若各数据具有不同的权值(拟合损失不同),权值为2, 2, 2, 1, 1,求加权二次最佳逼近。
I. 直接法
i. 二次最佳拟合,即求解线性回归方程 y = β 0 + β 1 x y = \beta_0 + \beta_1 x y=β0+β1x,由已知条件知
X = [ 1 − 2 1 − 1 1 0 1 1 1 2 ] , β = [ β 0 β 1 ] , y = [ 3 5 5 4 3 ] X=\left[\begin{array}{rr}1 &-2\\1 & -1\\1 &0\\1 &1\\ 1&2\end{array}\right],\quad \boldsymbol \beta=\left[\begin{array}{r}\beta_0\\\beta_1\end{array}\right],\quad \boldsymbol y = \left[\begin{array}{r}3\\5\\5\\4\\3\end{array}\right] X=⎣⎢⎢⎢⎢⎡11111−2−1012⎦⎥⎥⎥⎥⎤,β=[β0β1],y=⎣⎢⎢⎢⎢⎡35543⎦⎥⎥⎥⎥⎤
由 β ^ = ( X ⊤ X ) − 1 X ⊤ y \boldsymbol {\hat \beta}=(X^\top X)^{-1}X^\top \boldsymbol y β^=(X⊤X)−1X⊤y,得 β ^ = [ 4.0 , − 0.10 ] ⊤ \boldsymbol {\hat \beta}=[4.0, -0.10]^\top β^=[4.0,−0.10]⊤。
ii. 三次最佳拟合,即求解线性回归方程 y = β 0 + β 1 x + β 2 x 2 y = \beta_0 + \beta_1 x + \beta_2 x^2 y=β0+β1x+β2x2,由已知条件知
X = [ 1 − 2 4 1 − 1 1 1 0 0 1 1 1 1 2 4 ] , β = [ β 0 β 1 β 2 ] , y = [ 3 5 5 4 3 ] X=\left[\begin{array}{rr}1 &-2 &4\\1 & -1 &1\\1 &0 &0\\1 &1 &1\\ 1&2 &4\end{array}\right],\quad \boldsymbol \beta=\left[\begin{array}{r}\beta_0\\\beta_1\\\beta_2\end{array}\right],\quad \boldsymbol y = \left[\begin{array}{r}3\\5\\5\\4\\3\end{array}\right] X=⎣⎢⎢⎢⎢⎡11111−2−101241014⎦⎥⎥⎥⎥⎤,β=⎣⎡β0β1β2⎦⎤,y=⎣⎢⎢⎢⎢⎡35543⎦⎥⎥⎥⎥⎤
由 β ^ = ( X ⊤ X ) − 1 X ⊤ y \boldsymbol {\hat \beta}=(X^\top X)^{-1}X^\top \boldsymbol y β^=(X⊤X)−1X⊤y,得 β ^ = [ 5 , − 0.10 , − 0.5 ] ⊤ \boldsymbol {\hat \beta}=[5, -0.10, -0.5]^\top β^=[5,−0.10,−0.5]⊤。
II. 坐标向量法
多项式空间 P 3 \mathbb P_3 P3在-2,-1,0,1,2处的正交基 V = ( 1 , t , t 2 − 2 ) V = (1, t, t^2-2) V=(1,t,t2−2),因此, P 3 \mathbb P_3 P3内多项式对数据的最佳逼近,即正交投影 proj V y \text{proj}_V\boldsymbol y projVy
p ^ ( t ) = ⟨ y , p 0 ⟩ ⟨ p 0 , p 0 ⟩ p 0 + ⟨ y , p 1 ⟩ ⟨ p 1 , p 1 ⟩ p 1 + ⟨ y , p 2 ⟩ ⟨ p 2 , p 2 ⟩ p 2 = 4 − 0.1 t − 0.5 ( t 2 − 2 ) \hat p(t) = \frac{\langle y,p_0\rangle}{\langle p_0, p_0\rangle}p_0 +\frac{\langle y,p_1\rangle}{\langle p_1,p_1\rangle} p_1 +\frac{\langle y,p_2\rangle}{\langle p_2,p_2\rangle} p_2 =4 - 0.1t - 0.5(t^2-2) p^(t)=⟨p0,p0⟩⟨y,p0⟩p0+⟨p1,p1⟩⟨y,p1⟩p1+⟨p2,p2⟩⟨y,p2⟩p2=4−0.1t−0.5(t2−2)
III. 加权逼近
若计算误差时不同 b b b具有不同权重,最优解满足
min b ^ ∈ R n w 1 2 ( b 1 − b ^ 1 ) 2 + ⋯ + w n 2 ( b n − b ^ n ) 2 = min b ^ ∈ R n ∣ ∣ W b − W b ^ ∣ ∣ = min x ^ ∈ R n ∣ ∣ W b − W A x ^ ∣ ∣ \min_{\boldsymbol{\hat b} \in \R^n} w_1^2(b_1-\hat b_1)^2 + \cdots + w_n^2(b_n-\hat b_n)^2 = \min_{\boldsymbol{\hat b} \in \R^n}||W\boldsymbol b - W\hat{\boldsymbol b}|| = \min_{\boldsymbol{\hat x} \in \R^n}||W\boldsymbol b - WA\hat{\boldsymbol x}|| b^∈Rnminw12(b1−b^1)2+⋯+wn2(bn−b^n)2=b^∈Rnmin∣∣Wb−Wb^∣∣=x^∈Rnmin∣∣Wb−WAx^∣∣
将 W b W\boldsymbol b Wb在 W A WA WA的列空间中正交分解,最优解 x ^ \boldsymbol{\hat x} x^满足: ( W b − W A x ^ ) ⊥ Col W A (W\boldsymbol b - WA\boldsymbol{\hat x})\ \bot\ \text{Col }WA (Wb−WAx^) ⊥ Col WA,即
( W A ) ⊤ ( W b − W A x ^ ) = 0 ⟹ ( W A ) ⊤ W A x ^ = ( W A ) ⊤ W b (WA)^\top (W\boldsymbol b - WA\boldsymbol{\hat x})=\boldsymbol 0 \implies (WA)^\top WA\boldsymbol{\hat x}=(WA)^\top W\boldsymbol b (WA)⊤(Wb−WAx^)=0⟹(WA)⊤WAx^=(WA)⊤Wb
对于二次最近逼近,原问题的条件如下:
X = [ 1 − 2 1 − 1 1 0 1 1 1 2 ] , β = [ β 0 β 1 ] , y = [ 3 5 5 4 3 ] ⟹ W X = [ 2 − 4 2 − 2 2 0 1 1 1 2 ] , W y = [ 6 10 10 4 3 ] X=\left[\begin{array}{rr}1 &-2\\1 & -1\\1 &0\\1 &1\\ 1&2\end{array}\right],\quad \boldsymbol \beta=\left[\begin{array}{r}\beta_0\\\beta_1\end{array}\right],\quad \boldsymbol y = \left[\begin{array}{r}3\\5\\5\\4\\3\end{array}\right]\implies WX=\left[\begin{array}{rr}2 &-4\\2 & -2\\2 &0\\1 &1\\ 1&2\end{array}\right],\quad W\boldsymbol y = \left[\begin{array}{r}6\\10\\10\\4\\3\end{array}\right] X=⎣⎢⎢⎢⎢⎡11111−2−1012⎦⎥⎥⎥⎥⎤,β=[β0β1],y=⎣⎢⎢⎢⎢⎡35543⎦⎥⎥⎥⎥⎤⟹WX=⎣⎢⎢⎢⎢⎡22211−4−2012⎦⎥⎥⎥⎥⎤,Wy=⎣⎢⎢⎢⎢⎡6101043⎦⎥⎥⎥⎥⎤
通过法方程 ( W X ) ⊤ W X β ^ = ( W X ) ⊤ W y (WX)^\top WX\boldsymbol{\hat \beta} = (WX)^\top W\boldsymbol y (WX)⊤WXβ^=(WX)⊤Wy,得最小二乘解 β ^ = [ 4.30 0.20 ] ⊤ \boldsymbol{\hat \beta}=[4.30\quad 0.20]^\top β^=[4.300.20]⊤。
对称矩阵和二次型(Symmetric Matrices and Quadratic Forms)
定理1 如果 A A A是对称矩阵,则不同特征空间的任意两个特征向量正交。
证明:设 v 1 v_1 v1和 v 2 v_2 v2是对应于不同特征值 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2的特征向量,则
λ 1 v 1 ⋅ v 2 = ( λ 1 v 1 ) ⊤ v 2 = ( A v 1 ) ⊤ v 2 = ( v 1 ⊤ A ⊤ ) v 2 = v 1 ⊤ ( A v 2 ) = v 1 ⊤ ( λ 2 v 2 ) = λ 2 v 1 ⊤ v 2 = λ 2 v 1 ⋅ v 2 \lambda_1\boldsymbol v_1\cdot \boldsymbol v_2=(\lambda_1\boldsymbol v_1)^\top\boldsymbol v_2=(A\boldsymbol v_1)^\top \boldsymbol v_2=(\boldsymbol v_1^\top A^\top)\boldsymbol v_2=\boldsymbol v_1^\top(A\boldsymbol v_2)=\boldsymbol v_1^\top(\lambda_2\boldsymbol v_2)=\lambda_2\boldsymbol v_1^\top\boldsymbol v_2=\lambda_2\boldsymbol v_1\cdot \boldsymbol v_2 λ1v1⋅v2=(λ1v1)⊤v2=(Av1)⊤v2=(v1⊤A⊤)v2=v1⊤(Av2)=v1⊤(λ2v2)=λ2v1⊤v2=λ2v1⋅v2
由于 λ 1 \lambda_1 λ1不等于 λ 2 \lambda_2 λ2,因此 v 1 \boldsymbol v_1 v1和 v 2 \boldsymbol v_2 v2。
定理2 一个 n × n n\times n n×n矩阵 A A A可正交对角化的充要条件是 A A A是对称矩阵。
谱分解(Spectral Decomposition)
假设 A = P D P − 1 A=PDP^{-1} A=PDP−1,其中 P P P为单位正交矩阵,列向量为特征向量,因此 P − 1 = P ⊤ P^{-1}=P^\top P−1=P⊤,故
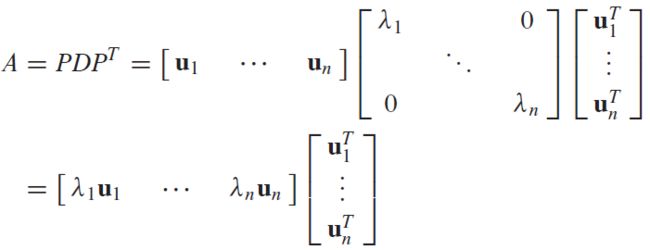
展开得
A = λ 1 u 1 u 1 ⊤ + λ 2 u 2 u 2 ⊤ + ⋯ + λ n u n u n ⊤ A=\lambda_1\boldsymbol u_1\boldsymbol u_1^\top + \lambda_2\boldsymbol u_2\boldsymbol u_2^\top+\cdots+\lambda_n\boldsymbol u_n\boldsymbol u_n^\top A=λ1u1u1⊤+λ2u2u2⊤+⋯+λnunun⊤
二次型(Quadratic Forms)
R n \R^n Rn上的二次型是一个定义在 R n \R^n Rn上的函数,若 n n n阶矩阵 A n × n A_{n\times n} An×n为对称矩阵,则二次型定义为
Q ( x ) = x ⊤ A x Q(\boldsymbol x)=\boldsymbol x^\top A \boldsymbol x Q(x)=x⊤Ax
若存在可逆矩阵 P P P,使得 x = P y x=Py x=Py,则
x ⊤ A x = ( P y ) ⊤ A ( P y ) = y ⊤ ( P ⊤ A P ) y = y ⊤ D y x^\top Ax=(Py)^\top A(Py)=y^\top(P^\top AP)y=y^\top Dy x⊤Ax=(Py)⊤A(Py)=y⊤(P⊤AP)y=y⊤Dy
由于 A A A是对称矩阵,因此存在正交矩阵 P P P,使得 P ⊤ A P P^\top AP P⊤AP为对角矩阵。也就是说,可利用变量代还,将含有交叉积的二次型转换为没有交叉积的二次型:

如对于二次型 Q ( x ) = x 1 2 − 8 x 1 x 2 − 5 x 2 2 Q(x)=x_1^2-8x_1x_2-5x_2^2 Q(x)=x12−8x1x2−5x22,对应的矩阵、特征向量和特征值
A = [ 1 − 4 − 4 − 5 ] , P = [ 2 / 5 1 / 5 − 1 / 5 2 / 5 ] , D = [ 3 0 0 − 7 ] A=\left[\begin{array}{r}1 &-4\\ -4 & -5\end{array}\right],\quad P=\left[\begin{array}{r}2/\sqrt 5 &1/\sqrt 5\\ -1/\sqrt 5 & 2/\sqrt 5\end{array}\right],\ D=\left[\begin{array}{r}3 &0\\ 0 &-7\end{array}\right] A=[1−4−4−5],P=[2/5−1/51/52/5], D=[300−7]
即 A = P D P − 1 A=PDP^{-1} A=PDP−1,且 D = P − 1 A P = P ⊤ A P D=P^{-1}AP=P^\top AP D=P−1AP=P⊤AP,使用变量代换 x = P y x=Py x=Py,则
x 1 2 − 8 x 1 x 2 − 5 x 2 2 = x ⊤ A x = ( P y ) ⊤ A ( P y ) = y ⊤ D y = 3 y 1 2 − 7 y 2 2 x_1^2-8x_1x_2-5x_2^2=x^\top Ax=(Py)^\top A(Py)=y^\top Dy=3y_1^2-7y_2^2 x12−8x1x2−5x22=x⊤Ax=(Py)⊤A(Py)=y⊤Dy=3y12−7y22
利用变换代换后的二次型计算 Q ( x ) Q(x) Q(x)在 x = ( 2 , − 2 ) x=(2,-2) x=(2,−2)时的值,由于 y = P − 1 x = P ⊤ x y=P^{-1}x=P^\top x y=P−1x=P⊤x,知
y = [ 6 / 5 , − 2 / 5 ] ⊤ ⟹ Q ( x ) = y 1 2 − 7 y 2 2 = 16 y=[6/\sqrt 5,\ -2/\sqrt 5]^\top \implies Q(x)=y_1^2-7y_2^2=16 y=[6/5, −2/5]⊤⟹Q(x)=y12−7y22=16
二次型分类
对于二次型 Q ( x ) = x ⊤ A x Q(\boldsymbol x)=\boldsymbol x^\top A \boldsymbol x Q(x)=x⊤Ax, λ i \lambda_i λi为 A A A的任一特征值,则二次型
- 正定, ∀ x ≠ 0 \forall \boldsymbol x\neq \boldsymbol 0 ∀x=0, Q ( x ) > 0 ⟺ λ i > 0 Q(\boldsymbol x) > 0 \iff \lambda_i > 0 Q(x)>0⟺λi>0;
- 负定, ∀ x ≠ 0 \forall \boldsymbol x\neq \boldsymbol 0 ∀x=0, Q ( x ) < 0 ⟺ λ i < 0 Q(\boldsymbol x) < 0 \iff \lambda_i < 0 Q(x)<0⟺λi<0;
- 不定, Q ( x ) Q(\boldsymbol x) Q(x)可正可负 ⟺ \iff ⟺ λ i \lambda_i λi有正有负;
条件优化
假设 A = A ⊤ A=A^\top A=A⊤, x ⊤ x = 1 \boldsymbol x^\top \boldsymbol x=1 x⊤x=1,求 arg max Q ( x ) = arg max x ⊤ A x \arg\max{Q}(\boldsymbol x)=\arg\max\boldsymbol x^\top A \boldsymbol x argmaxQ(x)=argmaxx⊤Ax ? 构造拉格朗日函数求极大值,如下
f ( x ) = x ⊤ A x − λ ( x ⊤ x − 1 ) f({\boldsymbol x}) = \boldsymbol x^\top A\boldsymbol x - \lambda(\boldsymbol x^\top \boldsymbol x - 1) f(x)=x⊤Ax−λ(x⊤x−1)
由
∂ f ∂ x = 2 A x − 2 λ x = 0 ⟹ A x = λ x \dfrac{\partial f}{\partial \boldsymbol x} = 2A\boldsymbol x - 2\lambda \boldsymbol x=0 \implies A\boldsymbol x=\lambda \boldsymbol x ∂x∂f=2Ax−2λx=0⟹Ax=λx
约束二次型在极值点处,满足 Q ( x ) = λ Q(\boldsymbol x)=\lambda Q(x)=λ ,即最大特征值及其对应的特征向量为极大解 λ 1 \lambda_1 λ1和解向量 u 1 \boldsymbol u_1 u1。构造拉格朗日求第二大,第二大解向量与极大解向量正交,如下
f ( x ) = x ⊤ A x − λ ( x ⊤ x − 1 ) − β ( x ⊤ u 1 − 0 ) f(\boldsymbol x)=\boldsymbol x^\top A\boldsymbol x - \lambda(\boldsymbol x^\top \boldsymbol x - 1) - \beta(\boldsymbol x^\top \boldsymbol u_1 - 0) f(x)=x⊤Ax−λ(x⊤x−1)−β(x⊤u1−0)
由
∂ f ∂ x = 2 A x − 2 λ x − β u 1 = 0 \dfrac{\partial f}{\partial \boldsymbol x} = 2A\boldsymbol x - 2\lambda \boldsymbol x - \beta\boldsymbol u_1=0 ∂x∂f=2Ax−2λx−βu1=0
上式左乘 u 1 ⊤ \boldsymbol u_1^\top u1⊤, u 1 ⊤ A x = x ⊤ λ 1 u 1 = 0 \boldsymbol u_1^\top A\boldsymbol x=\boldsymbol x^\top \lambda_1\boldsymbol u_1=0 u1⊤Ax=x⊤λ1u1=0,得 β = 0 \beta=0 β=0,因此 A x = λ x A\boldsymbol x=\lambda \boldsymbol x Ax=λx,第二大特征值及其特征向量为所求解。
奇异值分解(Singular Value Decomposition,SVD)
奇异值的应用
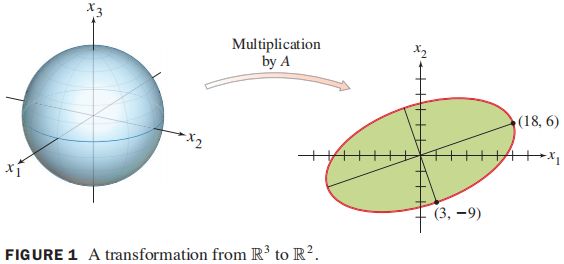
对于矩阵 A 2 × 3 A_{2\times 3} A2×3,线性变换 x ↦ A x \boldsymbol x\mapsto A\boldsymbol x x↦Ax,将 R 3 \R^3 R3中的单位球映射到 R 2 \R^2 R2中的椭圆,则 ∣ ∣ A x ∣ ∣ ||A\boldsymbol x|| ∣∣Ax∣∣最大的单位向量 x \boldsymbol x x是什么?最大长度是多少?
解: 该问题等价于求解 ∣ ∣ A x ∣ ∣ 2 ||A\boldsymbol x||^2 ∣∣Ax∣∣2,等价于求解在 ∣ ∣ x ∣ ∣ = 1 下 , ||\boldsymbol x||=1下, ∣∣x∣∣=1下, x ⊤ ( A ⊤ A ) x \boldsymbol x^\top(A^\top A)\boldsymbol x x⊤(A⊤A)x的最大值,显然最大值是 A ⊤ A A^\top A A⊤A的最大特征值,对应的向量为最大特征值对应的特征向量(长轴向量)。
矩阵奇异值分解常用于估算矩阵的秩,秩等价于非零奇异值数目。
矩阵的奇异值
对于矩阵 A m × n A_{m\times n} Am×n, [ A ⊤ A ] n × n [A^\top A]_{n \times n} [A⊤A]n×n为对称矩阵, { v 1 , ⋯ , v n } \{\boldsymbol v_1, \cdots, \boldsymbol v_n\} {v1,⋯,vn}是 R n \R^n Rn的单位正交基,且构成 A ⊤ A A^\top A A⊤A的特征向量, λ 1 ≥ ⋯ ≥ λ n \lambda_1\geq \cdots \geq \lambda_n λ1≥⋯≥λn是 A ⊤ A A^\top A A⊤A的特征值,则
∣ ∣ A v i ∣ ∣ 2 = ( A v i ) ⊤ A v i = v i ⊤ A ⊤ A v i = v i ⊤ λ i v i = λ i ≥ 0 (1) ||A\boldsymbol v_i||^2=(A\boldsymbol v_i)^\top A\boldsymbol v_i = \boldsymbol v_i^\top A^\top A\boldsymbol v_i = \boldsymbol v_i^\top \lambda_ i \boldsymbol v_i=\lambda_i\geq 0 \tag 1 ∣∣Avi∣∣2=(Avi)⊤Avi=vi⊤A⊤Avi=vi⊤λivi=λi≥0(1)
A A A的奇异值定义为 A ⊤ A A^\top A A⊤A特征值的平方根,也就是 A v A\boldsymbol v Av的长度,即
σ i = ∣ ∣ A v i ∣ ∣ = λ i , 1 ≤ i ≤ n \sigma_i =||A\boldsymbol v_i|| =\sqrt \lambda_i, \quad 1 \leq i \leq n σi=∣∣Avi∣∣=λi,1≤i≤n
定理: 若 A ⊤ A A^\top A A⊤A的特征值满足 λ 1 ≥ ⋯ ≥ λ r > 0 > λ n \lambda_1\geq \cdots \geq \lambda_r\gt 0\gt\lambda_n λ1≥⋯≥λr>0>λn, 则 { A v 1 , ⋯ , A v r } \{A\boldsymbol v_1,\cdots,A\boldsymbol v_r\} {Av1,⋯,Avr}是 Col A \text{Col }A Col A的标准正交基。
证明: A v A\boldsymbol v Av的模等于 A A A的奇异值(当前仅当向量为零向量时,模为零),当 r + 1 ≤ i ≤ n r+1\leq i\leq n r+1≤i≤n, A v i = 0 A\boldsymbol v_i=0 Avi=0,对于 x ∈ R n \boldsymbol x\in\R^n x∈Rn,有
A x = A ( c 1 v 1 + ⋯ + c n v n ) = c 1 A v 1 + ⋯ + c r A v r A\boldsymbol x=A(c_1\boldsymbol v_1+\cdots+c_n\boldsymbol v_n)=c_1A\boldsymbol v_1+\cdots+c_rA\boldsymbol v_r Ax=A(c1v1+⋯+cnvn)=c1Av1+⋯+crAvr
即对于任意 A A A列空间中向量 A x A\boldsymbol x Ax,均可由 { A v 1 , ⋯ , A v r } \{A\boldsymbol v_1,\cdots,A\boldsymbol v_r\}