蓝桥杯RepresentativeSampling与字典树
蓝桥杯RepresentativeSampling与字典树
1.相关参考
参考文章:字典树基础知识
参考代码:RepresentativeSampling参考代码来源
2.问题描述
【题目描述】
来自ABBYY的小明有一个与“细胞与遗传学研究所”的合作。最近,研究所用一个新的题目考验小明。题目如下。
有由n个细胞组成的一个集合(不一定不同)每个细胞是一个由小写拉丁字母组成的字符串。科学家给小明提出的问题是从给定集合中选出一个大小为k的子集,使得所选子集的代表值最大。
小明做了些研究并得出了一个结论,即一个蛋白质集合的代表制可以用一个方便计算的整数来表示。我们假设当前的集合为{a1, …, ak},包含了k个用以表示蛋白质的字符串。那么蛋白质集合的代表值可以用如下的式子来表示:
其中f(x, y)表示字符串x和y的最长公共前缀的长度,例如:
f(“abc”, “abd”) = 2 , f(“ab”, “bcd”) = 0.
因此,蛋白质集合{“abc”, “abd”, “abe”}的代表值等于6,集合{“aaa”, “ba”, “ba”}的代表值等于2。
在发现了这个之后,小明要求赛事参与者写一个程序选出,给定蛋白质的集合中的大小为k的子集中,能获得最大可能代表性值得一个子集。帮助他解决这个问题吧!
【输入格式】
输入数据第一行包含2个正整数n和k(1≤k≤n),由一个空格隔开。接下来的n行每一行都包含对蛋白质的描述。每个蛋白质都是一个仅有不超过500个小写拉丁字母组成的非空字符串。有些字符串可能是相等的。
输出格式
输出一个整数,表示给定蛋白质集合的大小为k的子集的代表值最大可能是多少。
3.问题分析
该问题实际上是在求所有字符串中最长公共子串长度相加之和;
如:蛋白质集合{“abc”, “abd”, “abe”}的代表值等于6,这个6为“abc”中的ab(2)+“abd”中的ab(2)+“abe”中的ab(2)=6
这个问题的有效解决方法就是前缀树,即字典树。
4.字典树简介
首先,我们通过图片对字典树有一个形象上的初步认识:

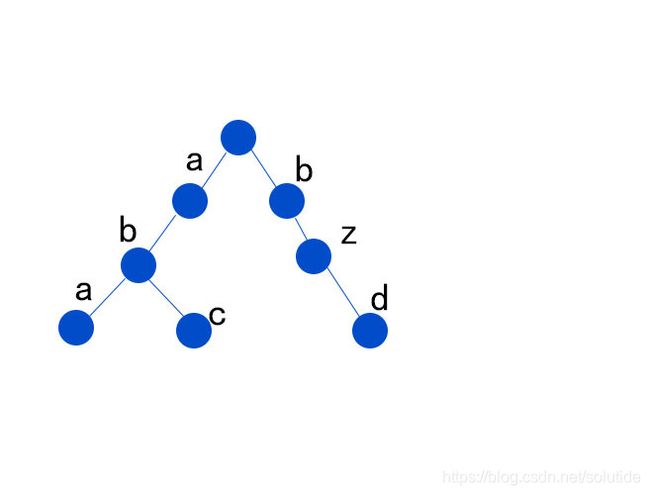
如图为两个字典树。
图一包含字符串“aaa”“abba”“abbc”“abbd”
图二包含字符串“aba”“abc”“bzd”
由图可以总结出,字典树的基本性质:
(1)根节点不包含字符,除根节点外每个节点只包含一个字符。
(2)从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
(3)每个节点的所有子节点包含的字符串不相同。
特性:
1)根节点不包含字符,除根节点外每一个节点都只包含一个字符。
2)从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
3)每个节点的所有子节点包含的字符都不相同。
4)如果字符的种数为n,则每个结点的出度为n,这也是空间换时间的体现,浪费了很多的空间。
5)插入查找的复杂度为O(n),n为字符串长度。
此处为简要摘录,关于字典树的更多具体内容与代码实现可查看顶部链接内博主的介绍。
5.RepresentativeSampling问题的代码分析
因链接二中原博只给出了蓝桥杯中上述问题的示范代码,所以我将自己对博主代码的理解与注释写出,方便大家理解,建立字典树与该问题初步的概念。
#include