随机蕨（Random Ferns）
转自：https://blog.csdn.net/huangynn/article/details/51730076
原作链接：http://cvlab.epfl.ch/alumni/oezuysal/ferns.html
一篇做人脸对齐的文章《Face Alignment by Explicit Shape Regression》使用了随机蕨来做人脸特征点的回归预测。
先回想一下随机森林。随机森林是很多棵决策树组成的，每颗决策树使用部分的训练样本以及部分的训练特征，并在此特征空间内按信息熵增益从小到大（特征区别度从大到小）来进行分支。最后的分类结果由多棵决策树共同表决，给出lable。
要理解随机蕨，需要了解两个部分，一个是特征，另一个是结构
朴素贝叶斯理论（Naive Bayesian）
要理解二元特征的构造，首先要从贝叶斯理论说起。
分类问题就是根据特征决定类别，也就是求后验概率。
根据贝叶斯定理，这个公式等价于 liklihood * prior:
然而要学习所有特征的联合分布几乎是不可能的，所以，如果特征之间是条件独立的联合分布就可以转换为以下问题（朴素贝叶斯假设）：
所以对于一个朴素贝叶斯（Naive Byesian ）来说，分类问题可以转化为：
然而一般情况下，特征之间不太可能都是条件独立的，所以以这种方式近似的话，会导致严重的后验概率的偏差。然而我们又很容易就能得到条件密度P(fi|Ck)P(fi|Ck), 从对样本集的统计中就可以得到。这种简单易用的估计方法我们想沿用，就必须提高其准确性，即提高特征之间的条件独立性，于是有了半朴素贝叶斯。
半朴素贝叶斯（Semi-Naive Bayesian）
把一组特征分成LL 个小子集，每个子集的大小是 SS （蕨，ferns）
其中 fnfn 是二元特征，即 fn:{0,1}fn:{0,1}
假设这些特征组之间是独立的，即
在此条件下的分类问题即为：
半朴素贝叶斯可以看成是复杂度和近似程度之间的trade off，可以通过选择合适的 fern size（S）和 num ferns （L）来进行平衡。
fern简介
单棵fern特征提取
fern会在输入的样本中进行S个二元测试，如下图所示, 当蓝色点所在的像素值大于红色点所在的像素值则二元测试结果为1，反之为0 。 
进行S个二元测试后，测试所得的feature必然落入[0,2s−1][0,2s−1] 之间。 
当输入多个训练样本后，fern上的输出是一个多项式分布。 
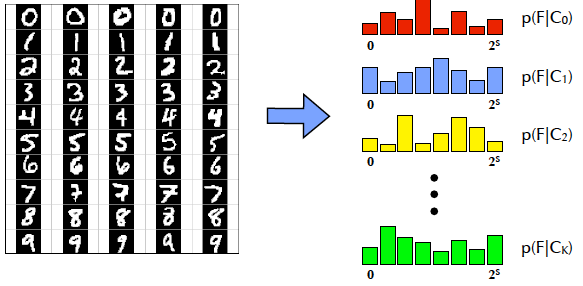
训练fern
把各个类别的训练样本对Dm=(Im,Cm)Dm=(Im,Cm)都输入一个fern，并且计算其输出，这样就可以得到在各个类别上的多项式分布p(F|Ck)p(F|Ck).
使用fern分类
如下图所示，首先提取特征F(I)，在每个类别的多项式分布上都会输出一个p(F|Ci)p(F|Ci) ，再把新得到的分布归一化后就可以得到此样本属于各个类别的概率值了。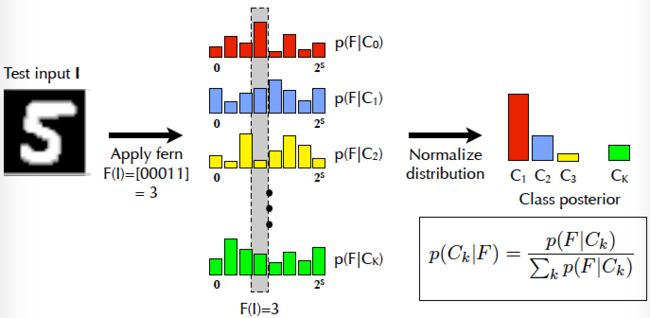 
随机蕨丛林构建
一棵蕨的分类效果难以让人满意，因此我们可以以随机森林的思路，构建随机蕨丛林。 
构建的方式就是通过随机的选择特征的子集。然后通过半朴素贝叶斯的方式求取最终的分类结果。
随机蕨丛林分类
至此，一个属于样本的标签取决于所有fern的输出的概率乘积乘以每个类别的先验概率。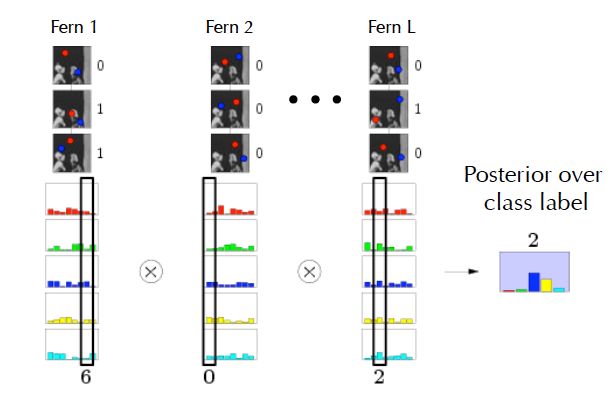 
一个小问题
即使是很小的fern size， S = 10, 得到的特征向量的范围会是[0, 1023] 。
因此，即使是训练集非常大，也可能会有一些样本落入的特征取值中的样本数目为0.
因此假设在P(F|Ck)P(F|Ck) 有狄利克雷先验分布。
假设所有的fern的输出中都有一个较低的base概率值。
其中N(F=z|Ck)N(F=z|Ck) 是观察到的特征值z属于CkCk的次数。
随机蕨与随机森林对比
| 随机森林 | 随机蕨 |
|---|---|
| 直接学习后验概率P(Ck|F)P(Ck|F) | 学习的是类条件分布 P(F|Ck)P(F|Ck) |
| 在每个子节点进行的序列test不一样（进入不同分支了） | 对每个输入样本执行的序列test都一致 |
| 随着树深度增加，训练时间指数级增长 | fern size增加，训练耗时线性增长 |
| 最终类别由每棵树输出的均值决定 | 使用贝叶斯定理来综合每个fern的输出得到最终结果 |
fern Vs tree 
随机蕨算法总结
1.易于理解，容易训练
2.分类速度非常快
3.提供概率性的输出
4.非常占用内存
fern size = 11
number of ferns = 50
number of classes = 1000
ram = 2^11 * 50 * 1000 * sizeof(float)
= 400 M